How to Use a Direct Variation Worksheet to Understand the Concept of Direct Variation.

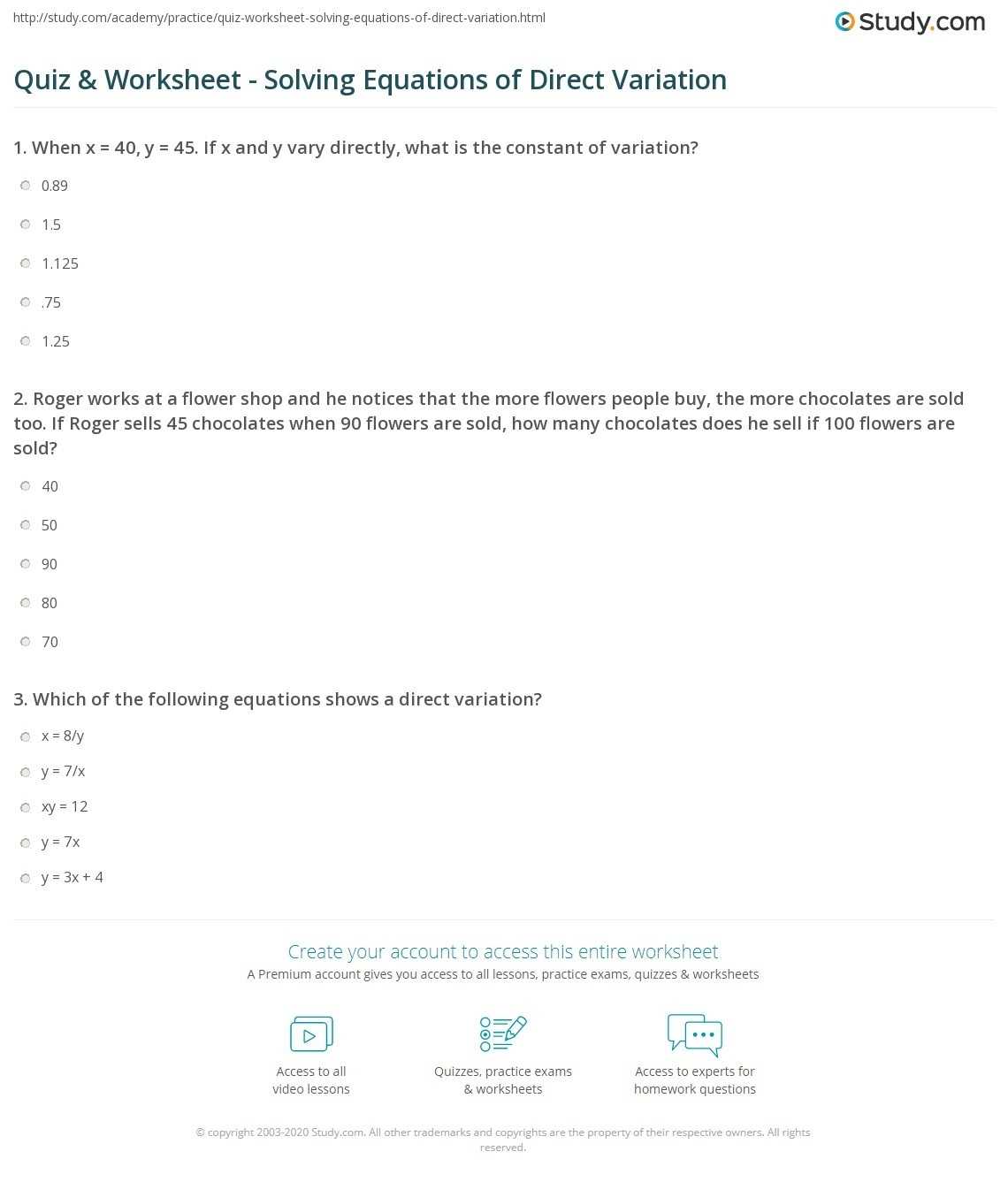
A direct variation worksheet is a useful tool for students to learn about the concept of direct variation. It is a type of mathematical equation that expresses a linear relationship between two variables. The worksheet helps students understand the principles of direct variation by providing them with problems that require them to calculate the constant of variation.

A direct variation worksheet typically consists of two columns, each containing a set of two variables. Students are asked to identify the constant of variation by comparing the values of the two variables in each row. To do this, students must first determine the value of one variable and then use that value to calculate the value of the other variable. For example, if the worksheet shows that x = 5 and y = 10, then the constant of variation would be 2.

The worksheet then provides students with a set of equations that require them to calculate the value of the constant of variation. These equations may include linear equations, exponential equations, and logarithmic equations. By providing students with these equations, they can better understand the concept of direct variation.

In addition to providing students with equations, the direct variation worksheet also provides a variety of practice problems. These problems require students to calculate the constant of variation by comparing the values of two variables in each row. This helps students gain a better understanding of the principles of direct variation.

By using a direct variation worksheet, students can gain a better understanding of the concept of direct variation. Through the use of equations and practice problems, students can better understand the principles of direct variation and gain a better understanding of how to use it in real-world applications.

Exploring the Different Types of Direct Variation Problems and Their Solutions.

Direct variation is a mathematical relationship between two variables, where one is a constant multiple of the other. This type of relationship is represented by the equation y = kx, where k is the constant of variation and x and y are the two variables. This equation shows that the value of one of the variables is directly proportional to the other, meaning that if one increases, the other will also increase and vice versa.

There are several different types of direct variation problems and their solutions. The most common type is the simple direct variation problem, which involves finding the constant of variation k. To do this, two points on the graph must be identified and the equation y = kx can be used to find the constant. For example, if the points (2, 4) and (4, 8) are given, the equation y = kx can be used to calculate that the constant of variation is 2.

Another type of direct variation problem is a joint direct variation problem. This type of problem deals with finding the constant of variation when two variables are directly proportional to each other. To solve this type of problem, three points on the graph must be identified. The equation y = kxz can be used to find the constant of variation k. For example, if the points (2, 4, 10), (3, 6, 15), and (4, 8, 20) are given, the equation y = kxz can be used to calculate that the constant of variation is 5.

Finally, a mixture direct variation problem involves finding the constant of variation when three variables are in a direct variation relationship. To solve this type of problem, four points on the graph must be identified and the equation y = kxyz can be used to calculate the constant of variation k. For example, if the points (2, 4, 10, 20), (3, 6, 15, 30), (4, 8, 20, 40), and (5, 10, 25, 50) are given, then the equation y = kxyz can be used to calculate that the constant of variation is 5.

In conclusion, direct variation is an important mathematical concept that can be used to solve a variety of real-world problems. There are several different types of direct variation problems, each of which requires a different equation and set of points to solve. By understanding the different types of direct variation problems and their solutions, students can better prepare themselves for future mathematical challenges.

Tips and Tricks for Working Out the Answers to Direct Variation Worksheets.

When tackling direct variation worksheets, there are several tips and tricks that can be employed to help arrive at the correct answers.

First and foremost, it is important to remember that in direct variation, there is a constant ratio between two variables. That is, one variable is always scaled up or down in proportion to the other. It is helpful to create a table that lists both variables and their corresponding values, as this can make the relationship between the two much clearer.

It is also helpful to use diagrams or graphs to represent the direct variation. Graphs are particularly useful for representing the data in an easily understandable way. Additionally, understanding the concept of slope can help to identify the correct answer. Slope is determined by the ratio of the change of one variable to the change of the other. If the ratio is constant, then the slope is also constant.

Finally, it is important to pay attention to the units of the variables in the equation. If the units are not consistent, the equation will not be valid. By understanding the relationship between the two variables and the units they are expressed in, it is much easier to solve the equation correctly.

By following these tips and tricks, it is possible to work out the answers to direct variation worksheets correctly and efficiently.

Examining the Applications of Direct Variation Worksheets in Real-World Settings.

Direct variation worksheets can be used in a variety of real-world settings to help students understand how values can vary based on a given set of conditions. Direct variation is a mathematical concept that focuses on the relationship between two variables. It states that when one variable increases, the other decreases or vice versa. By studying these worksheets, students can learn how to identify direct variation in everyday situations and apply it to their own experiences.

In the classroom, direct variation worksheets can be used to help students understand how two unrelated variables may be related. By plotting the variables on a graph, students can see how one variable affects the other. This can be used to demonstrate how changes in one variable can cause changes in another. For instance, if a student is studying the relationship between the amount of time spent studying and a student’s grade in a class, they can use a direct variation worksheet to plot the two variables and observe the resulting pattern.

Outside of the classroom, direct variation worksheets can also be used to help people apply the concept to their own lives. For instance, if a person wants to save money on their monthly expenses, they can use a direct variation worksheet to plot the cost of their items against the money they have available to spend. This can help them determine which items they should reduce or increase their spending on to stay within their budget.

Direct variation worksheets can also be used to help people understand the relationship between two different types of data. For example, a person might want to understand the relationship between the amount of time spent exercising and the amount of weight they lose. By plotting the two variables on a graph, they can observe the resulting pattern and determine what factors are influencing the outcome.

Overall, direct variation worksheets can be a useful tool for students and adults alike. By studying these worksheets, individuals can gain a better understanding of how two variables interact and apply the knowledge to their own lives. Through this knowledge, they can make more informed decisions about how to manage their resources and reach their goals.

An Overview of the Benefits of Working Through Direct Variation Worksheets.

Direct variation worksheets are an invaluable tool for those looking to understand and practice the concept of direct variation. Direct variation is a mathematical relationship between two variables where one of the variables is a constant multiple of the other. A direct variation equation is written as y = kx, where k is a constant.

Direct variation worksheets offer numerous benefits in helping students understand and practice direct variation. First, worksheets provide students with an opportunity to practice solving direct variation equations. This practice helps students become familiar with the process of solving direct variation equations and builds their problem-solving skills.

Second, direct variation worksheets help students visualize the relationship between two variables and how changes in one variable will affect the other. Students can see the effects of changing the constant in a direct variation equation and how that affects the graph of the equation.

Third, direct variation worksheets help students think critically about the relationship between two variables. Students learn to recognize the relationship between the two variables and analyze the effects of changing the constant in the equation. This helps them gain an understanding of the concept of direct variation and how it is used in real-world applications.

Finally, direct variation worksheets are an excellent way for students to practice and review their understanding of direct variation. By completing these worksheets, students can identify any areas in which they need to review or practice further.

Overall, direct variation worksheets are an invaluable tool for those looking to understand and practice the concept of direct variation. They provide students with an opportunity to practice solving direct variation equations, visualize the relationship between two variables, and think critically about the relationship between the two variables. In addition, they offer a great way for students to practice and review their understanding of direct variation.

Analyzing the Different Types of Direct Variation Problems With Sample Solutions.

Direct variation problems are those in which two variables are related in a linear fashion. In other words, if one variable increases, the other increases in direct proportion. This type of variation is represented mathematically as an equation of the form y = kx, where k is the constant of proportionality and x is an independent variable.

The most common type of direct variation problem is one in which the two variables are given in a table of values and the constant of proportionality must be calculated. In order to solve this kind of problem, the student must first calculate the ratio between the two variables for each pair of values in the table. Once the ratio is calculated, the constant of proportionality can be determined. For example, consider the following problem:

Given the following table of values, calculate the constant of proportionality:

x 2 5 7 10
y 8 20 28 40

In this situation, the student must first calculate the ratio between the two variables for each pair of values in the table. For the first pair of values, the ratio is 8/2 = 4. For the second pair of values, the ratio is 20/5 = 4. For the third pair of values, the ratio is 28/7 = 4. Finally, for the fourth pair of values, the ratio is 40/10 = 4. Since all of the ratios are equal, the constant of proportionality is equal to 4. The equation of direct variation for this problem is y = 4x.

Another type of direct variation problem is one in which the equation of direct variation is given, and the student must calculate the value of one or both variables. For example, consider the following problem:

Given the equation of direct variation y = 9x, what is the value of y when x = 6?

In this situation, the student must calculate the value of y using the equation of direct variation. Since the equation is y = 9x, the value of y when x = 6 is y = 9(6) = 54.

A third type of direct variation problem is one in which the equation of direct variation is given, and the student must calculate the constant of proportionality. For example, consider the following problem:

Given the equation of direct variation y = 3x, calculate the constant of proportionality.

In this situation, the student must calculate the constant of proportionality by examining the equation. Since the equation is y = 3x, the constant of proportionality is equal to 3.

Understanding the Important Concepts Behind Direct Variation Worksheets.

Direct variation is an important concept in mathematics. It is a type of linear relationship between two variables, where one variable is a multiple of the other. Direct variation worksheets are designed to help students understand this concept and its applications.

Direct variation worksheets typically begin by introducing the concept of direct variation and providing examples. The worksheets then move on to ask students to solve equations that represent direct variation relationships. These equations can be of the form y = kx, where k is a constant, and x is a variable. Students are asked to identify the constant and determine the relationship between the variables.

In addition to solving equations, direct variation worksheets also ask students to graph a direct variation equation. This allows students to visualize the relationship between the variables. By plotting points on the graph, students can determine the slope of the line and compare it to the constant. This helps students to understand the concept of direct variation and how it can be used to solve problems.

Direct variation worksheets can also ask students to use direct variation to solve problems. For example, students might be asked to solve a problem involving cost and quantity. They would use the equation y = kx to determine the cost of a certain number of items. By understanding this concept, students can understand how relationships between two variables can be used to solve real-world problems.

Direct variation worksheets can also be used to help students understand how to use direct variation to solve different types of problems. By solving equations that involve both linear and nonlinear relationships, students can gain a deeper understanding of direct variation and its applications.

Direct variation worksheets are a great way for students to gain a deeper understanding of an important mathematical concept. By understanding direct variation and its applications, students can use this concept to solve real-world problems. With practice, students can become comfortable with the concept and use it to their advantage in various situations.

Taking a Close Look at the Different Types of Direct Variation Problems and Their Solutions.

Direct variation is an algebraic relationship between two variables in which one is proportional to the other. This means that when one variable increases, the other increases proportionally, and if one decreases, the other decreases in the same proportion. This type of relationship is represented mathematically by the equation y = kx, where k is a constant.

There are several types of direct variation problems that can be solved using this equation. When the equation is given in the form y = kx, the problem is known as a direct variation problem in standard form. This type of problem involves finding the constant of proportionality k, given two points on the graph of the equation. For example, if we are given two points (2, 4) and (4, 8), we can solve for k by substituting the x-values and y-values into the equation and solving for k. In this example, k = 2, since 4 = 2(2) and 8 = 2(4).

Another type of direct variation problem is a direct variation problem in point-slope form. This type of problem requires finding the equation of a line given a point and its slope. For example, if we are given the point (2, 4) and the slope m = 2, then the equation of the line is y = 2x + 4. The constant of proportionality in this case is k = 2.

Finally, there is a type of direct variation problem known as a direct variation problem in slope-intercept form. This type of problem requires finding the equation of a line given its slope and y-intercept. For example, if we are given the slope m = 2 and the y-intercept b = 4, then the equation of the line is y = 2x + 4. Again, the constant of proportionality in this case is k = 2.

In summary, there are three main types of direct variation problems that can be solved using the equation y = kx. These are direct variation problems in standard form, point-slope form, and slope-intercept form. All three types of problems involve finding the constant of proportionality k, given either two points or a point and its slope, or the slope and y-intercept, respectively.

Conclusion

In conclusion, the Direct Variation Worksheet Answers provide students with an excellent opportunity to practice and review the concept of direct variation. The worksheet provides a variety of questions that cover the basics of direct variation and its applications to real-world problems. By completing the worksheet, students can gain a better understanding of direct variation and can learn to apply it to a variety of situations.