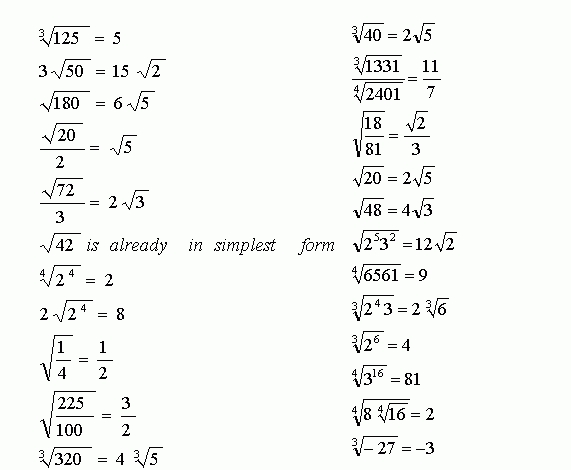The Benefits of Using a Simplifying Radicals Worksheet to Enhance Math Skills

The use of a simplifying radicals worksheet can be an effective tool for enhancing math skills. A simplifying radicals worksheet can help students practice and apply the concepts of simplifying radicals, which is a key component of algebraic equations.

Simplifying radicals can be a difficult concept to grasp, as it requires the student to factor, reduce and combine radicals. The student must also be able to identify the properties of radicals, including the product rule, the power rule, and the division rule. Simplifying radicals is a critical component of algebraic equations, as it can be used to solve equations and simplify expressions.

Using a simplifying radicals worksheet can be a great way for students to practice and apply the concepts of simplifying radicals. The worksheet can provide students with an opportunity to practice their simplifying skills, as well as an opportunity to compare their answers to the correct answer. Additionally, the worksheet can help students to become familiar with the properties of radicals, allowing them to better understand how to simplify expressions and solve equations.

[toc]

Moreover, the use of a simplifying radicals worksheet can be beneficial to students who are preparing for standardized tests. Many standardized tests require the student to solve equations and simplify expressions, and the use of a simplifying radicals worksheet can help students hone their skills in this area. Students can use the worksheet to practice and become familiar with the concepts of simplifying radicals prior to taking a standardized test.

In conclusion, the use of a simplifying radicals worksheet can be a valuable tool for enhancing math skills. The worksheet can provide students with an opportunity to practice and apply the concepts of simplifying radicals, allowing them to better understand how to simplify expressions and solve equations. Additionally, the worksheet can be beneficial to students who are preparing for standardized tests, as it can help them become familiar with the concepts prior to taking the test.

Exploring Strategies for Easily Solving Problems with Simplifying Radicals Worksheets

Radicals, or root expressions, are a critical component of mathematics. While they are sometimes difficult to solve, a few strategies can make the process much easier, especially when using a simplifying radicals worksheet.

First, it is important to understand the basics of radicals. In mathematics, a radical is a mathematical expression with a value that is the root of a number. For example, the square root of 25 is 5, and the cube root of 27 is 3. When simplifying radicals, the goal is to break down the expression into its simplest form.

One of the most effective strategies for simplifying radicals is to factor the number. To do this, divide the number into two or more factors that, when multiplied together, yield the original number. For example, the radical 25 can be factored into 5 x 5, and the radical 27 can be factored into 3 x 3 x 3. Once the number has been factored, the radical can be broken down into the product of the factors.

Another helpful strategy is to use the index law. This law states that if an expression is raised to a power, then the radical can be reduced to the power of the index. For example, the expression x^12 can be simplified to x^4 because the index of the radical is 4.

A third strategy is to use the conjugate. This law states that, if two numbers are multiplied together, then the radical of the product can be rewritten as the product of the radicals. For example, if two numbers, x and y, are multiplied together, then the radical of their product can be written as the radical of x times the radical of y.

Finally, it is helpful to use the rational exponents law. This law states that, if an expression is raised to a power, then the radical can be written as a fractional exponent of the same base. For example, if an expression is raised to the power of 4/3, then the radical can be written as the fractional exponent (1/3) of the same base.

By understanding and utilizing these strategies, simplifying radicals worksheets can become much easier to complete. With practice and dedication, students can quickly and effectively master radical expressions.

Teaching Tips for Making Simplifying Radicals Practice Worksheets Engaging for Students

1. Emphasize the importance of understanding the concept: Explain to students why it is important to simplify radicals and how they will be able to use this knowledge in higher level math classes.

2. Provide visuals: Use illustrative diagrams and visuals to help students understand the concepts.

3. Incorporate real-world examples: Provide examples of how simplifying radicals can be applied to everyday life.

4. Make use of practice problems: Provide practice problems with varying degrees of difficulty to help students improve their skills.

5. Promote collaboration: Encourage students to work together to solve the practice problems by providing a worksheet that is designed for small groups or pairs.

6. Use games and puzzles: Incorporate fun activities like crosswords or word searches that involve simplifying radicals to make the learning process more engaging.

7. Offer incentives: Offer rewards or incentives to encourage students to complete the practice worksheets.

8. Provide feedback: Give feedback and provide helpful tips on how to simplify radicals to help students understand the topic more effectively.

Conclusion

In conclusion, simplifying radicals practice worksheet can be a great way to help students understand the concept of simplifying radicals. It can also help them understand the importance of following the steps correctly and understanding the process of simplifying radicals. By providing practice problems, students can better grasp the concept of simplifying radicals, which will ultimately help them in their future math studies.

[addtoany]