Understanding How to Solve a Multiplying Polynomials Worksheet: Tips and Strategies

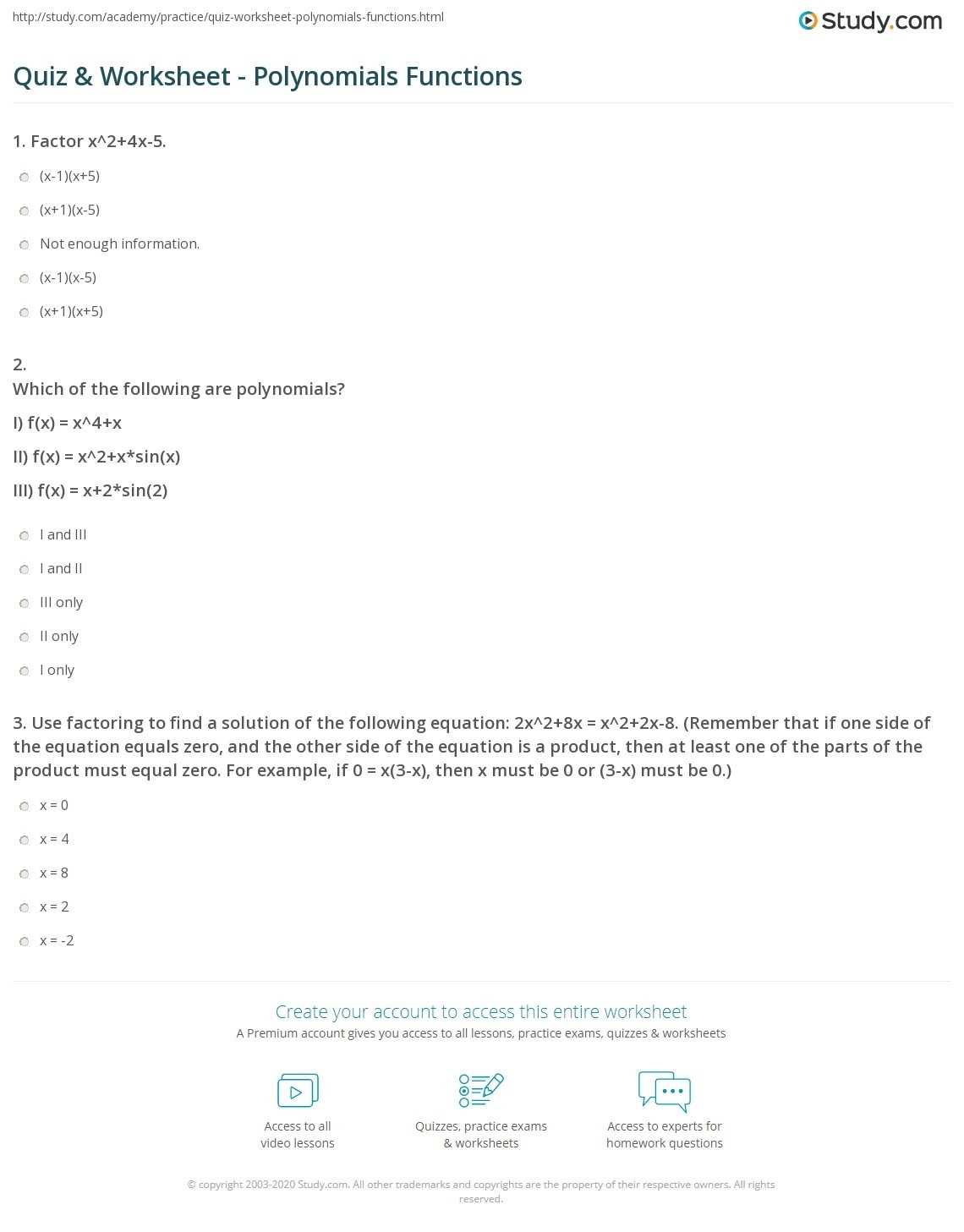
When solving a multiplying polynomials worksheet, it is important to understand the basic principles of polynomial multiplication. Multiplying polynomials involves taking two or more polynomials and multiplying each of their terms together. To solve a multiplying polynomials worksheet, students must use the rules of multiplication and understand how to use the FOIL method.

The FOIL method stands for First, Outer, Inner, and Last. This method applies when multiplying two binomials, which are polynomials with two terms. To use the FOIL method, students must multiply the first term of the first polynomial with the first term of the second polynomial. This is known as the first product. Then, students must multiply the first term of the first polynomial with the last term of the second polynomial. This is known as the outer product. Next, students must multiply the last term of the first polynomial with the first term of the second polynomial. This is known as the inner product. Finally, students must multiply the last term of the first polynomial with the last term of the second polynomial. This is known as the last product.

When solving a multiplying polynomials worksheet, students must also understand how to use the distributive property. The distributive property states that when two numbers are multiplied, one number can be distributed to each of the terms in the other number. To use the distributive property, students must multiply each term in one polynomial with each term in the other polynomial and then add the products. This can be done by breaking the problem down into smaller parts and solving each part separately.

[toc]

When solving a multiplying polynomials worksheet, it is important to pay close attention to the order of operations. Order of operations is a set of rules that determine which operations to complete first and which operations to complete last. The order of operations states that multiplication and division should be completed before addition and subtraction. To ensure accuracy when solving a multiplying polynomials worksheet, students should perform all operations in the order specified.

Finally, when solving a multiplying polynomials worksheet, students should always check their work for accuracy. This can be done by comparing the answer to the original problem. If the answer does not match, students should go back and double-check their work to ensure that no mistakes were made.

By following these tips and strategies, students can successfully solve a multiplying polynomials worksheet. Understanding the FOIL method, the distributive property, and the order of operations are essential for accurately solving a multiplying polynomials worksheet. Additionally, double-checking work is essential for obtaining the right answer.

Exploring Common Mistakes in Multiplying Polynomials Worksheets and How to Avoid Them

Multiplying polynomials is a complex mathematical operation that can be difficult to understand. To help students master this concept, many educators utilize worksheets to help students practice. However, as with any educational tool, there are common mistakes that students often make when completing these worksheets. As such, it is important for educators to be aware of these common mistakes and how to prevent them.

One of the most common mistakes made on multiplying polynomials worksheets is failing to properly multiply the exponents. When multiplying polynomials, the exponents of two terms must be multiplied together. For example, when multiplying (2×2)(3×2), the exponents must be multiplied together to be 4, thus the answer is 6×4. Failing to do this can lead to incorrect answers. To prevent this mistake, educators should ensure that students understand the rules of exponents and provide examples of multiplying polynomials with exponents.

Another common mistake made on polynomials worksheets is failing to properly distribute the terms when multiplying. In the example above, the students must multiply each term in the first polynomial with each term in the second polynomial. Failing to do this can lead to incorrect answers. To prevent this mistake, educators should emphasize the importance of correctly distributing terms when multiplying polynomials.

A third common mistake made on polynomials worksheets is forgetting to combine like terms. When multiplying polynomials, students must remember to combine like terms after multiplying. For example, if the answer to the example above is 6×4 + 6×2, the student must remember to combine the two 6x terms to make 12×2. Failing to do this can lead to incorrect answers. To prevent this mistake, educators should ensure that students understand the concept of combining like terms and provide examples of combining like terms after multiplying polynomials.

In conclusion, multiplying polynomials can be challenging for students. To help students master this concept, many educators utilize worksheets. However, there are common mistakes that students often make when completing these worksheets. To prevent these mistakes, educators should ensure that students understand the rules of exponents, the importance of correctly distributing terms, and the concept of combining like terms. By doing so, educators can help students avoid common mistakes and achieve success with their polynomials worksheets.

Utilizing Technology to Find Accurate Answers for Multiplying Polynomials Worksheets

The use of technology in the education sector has been on the rise in recent years, allowing for more efficient, accurate and effective teaching and learning. In particular, technology has been invaluable in helping students to understand and solve complex mathematical problems, such as those often found in multiplying polynomials worksheets.

In order to make the process of finding accurate answers for multiplying polynomials worksheets more efficient, there are a variety of online tools and software available. These tools and software can be used to generate accurate solutions for a variety of different polynomial equations, allowing for a more comprehensive understanding of the concepts involved.

For example, there are online calculators and graphing software that can help students to visualize and analyze the equation, allowing them to gain a better understanding of the problem. Students can then use the calculator to input the polynomial equation and the software will generate an accurate answer.

Moreover, there are also websites that offer interactive tutorials and simulations to help students practice their solving skills and gain a better understanding of the concepts involved in multiplying polynomials. These tutorials and simulations can be used to help students work through the equations step-by-step, allowing them to gain a better understanding of the fundamentals before attempting to solve the equation.

Finally, there are also online communities that offer students the opportunity to ask questions and get help from other students and professionals on topics related to multiplying polynomials. This can be invaluable for students who may be struggling to understand the concept, as the help and advice from more experienced peers can be invaluable.

Overall, technology has made it easier for students to learn and understand complex mathematical concepts, such as those found in multiplying polynomials worksheets. Through the use of online tools, software, tutorials and simulations, as well as online communities, students can now find accurate and efficient solutions for a variety of polynomial equations.

Conclusion

The Multiplying Polynomials Worksheet Answers provides an effective way to practice multiplying polynomials and gain a better understanding of the math concept. By solving the worksheet problems, students can become more confident in their ability to multiply polynomials and apply the math concept to real-world situations. With regular practice, students can become proficient in multiplying polynomials and gain a deeper understanding of the math concept.

[addtoany]