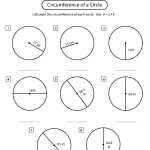
Exploring Angles in a Circle Worksheet: A Comprehensive Guide on How to Master the Concept

The concept of angles in a circle can be daunting for many students, especially those just beginning to learn geometry. Mastering this concept is essential for success in higher-level math classes. This worksheet is designed to provide an in-depth guide on how to understand and calculate angles in a circle.

This worksheet begins by introducing the concept of angles in a circle. It explains how the angle inside of a circle is measured using the central angle and the arc length. It also introduces the common terms used to describe angles in a circle, such as inscribed angle, central angle, and intercepted arc.

The worksheet then moves on to calculating angles in a circle. It provides step-by-step instructions on how to calculate an inscribed angle, central angle, and intercepted arc. It also includes sample problems to help students practice their skills.

[toc]

The worksheet concludes with a review of the key concepts. It includes a summary of the angle measurements and how they can be used to solve a variety of problems. It also provides tips and tricks for mastering angles in a circle.

This worksheet is a comprehensive guide on how to understand and calculate angles in a circle. With the help of this worksheet, students will gain a better understanding of this concept and be able to apply it to other mathematical problems.

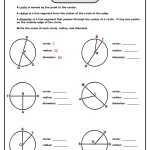
Understanding Angles in a Circle Worksheet: A Step-by-Step Guide to Finding the Right Measurements

Understanding angles in a circle can be an intimidating concept for many students. This worksheet is designed to help you gain a better understanding of angles in a circle so that you can find the right measurements for any given circle.

The worksheet begins by introducing the concept of angles in a circle and how they are measured. You will learn how the center of a circle is known as the vertex and how angles are formed by two rays that originate from the vertex. You will also learn the different types of angles, including central angles, inscribed angles, and intercepted arcs.

The worksheet then moves on to the different formulas used to find the measurements of angles in a circle. Firstly, you will learn the formula for finding the measure of an angle formed by two chords. This formula is used to find the measure of the angle formed by two chords that intersect within a circle. The worksheet also explains how to find the measure of an angle formed by a tangent and a chord. You will also learn how to find the measure of a central angle using the formula for central angles.

The worksheet then moves on to finding the measure of inscribed angles. You will learn how to find the measure of an inscribed angle using the formula for inscribed angles. You will also learn how to find the measure of an angle formed by two intersecting arcs. Finally, you will learn how to find the measure of an angle formed by three or more intersecting arcs.

This worksheet is designed to help you understand angles in a circle so that you can find the right measurements for any given circle. With a better understanding of angles in a circle, you will be better equipped to solve any problems related to angles in a circle.

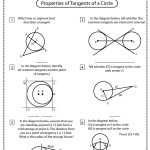
Unpacking the Angles in a Circle Worksheet: Tips on Interpreting the Diagrams

The Angles in a Circle worksheet is a useful tool for understanding the properties of angles and their relationships in a circle. This worksheet provides diagrams and equations to help students interpret and analyze the angles in a circle.

When interpreting the diagrams on the Angles in a Circle worksheet, it is important to take note of the angles that are provided. Each angle has unique characteristics that can be identified by its size, shape, and orientation.

It is also important to note the labeling of the angles. Each angle is labeled with a letter, such as A, B, or C. This letter helps to identify each angle and to distinguish them from one another.

For each diagram, the equation associated with the angles is also provided. This equation is important for understanding the relationships between the angles and for finding the measure of each angle.

It is also important to remember the properties of angles in a circle. Angles in a circle have a sum of 360 degrees, and a central angle is equal to twice the measure of its intercepted arc. All of these properties are important to understand when interpreting the diagrams on the Angles in a Circle worksheet.

By taking note of the angles and equations provided, following the labeling of the angles, and remembering the properties of angles in a circle, students can accurately interpret the diagrams on the Angles in a Circle worksheet. With practice and careful analysis, students can gain a deeper understanding of the properties of angles in a circle.

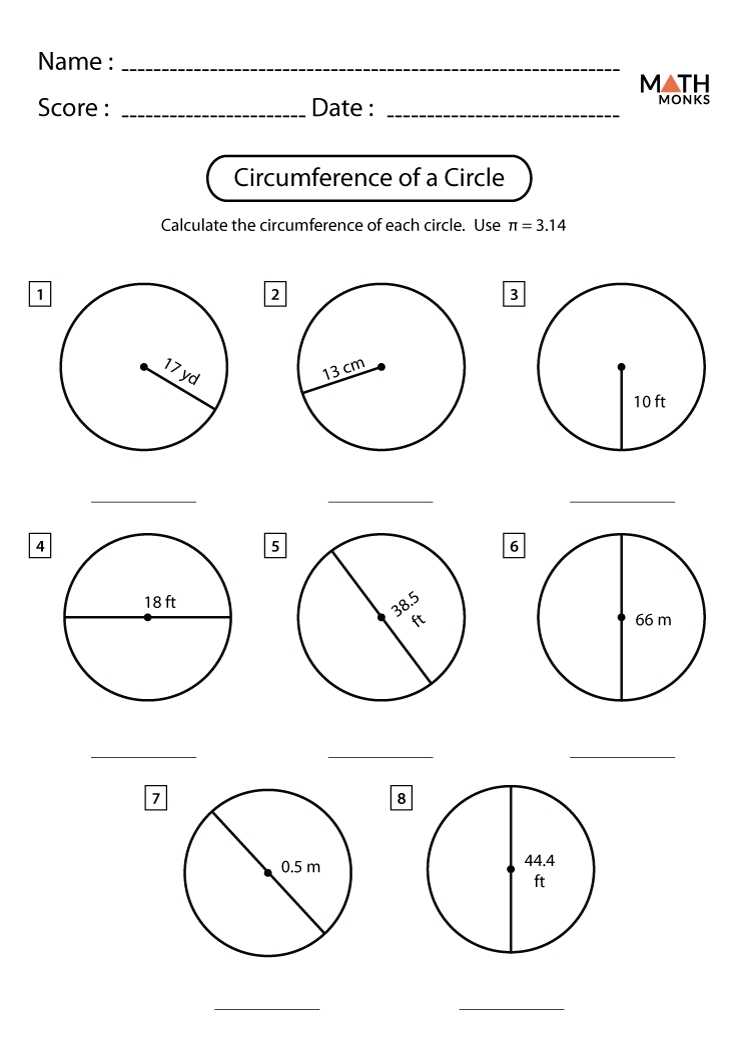
Analyzing Angles in a Circle Worksheet: A Comprehensive Overview of the Formulas and Applications

The worksheet begins with a definition of a circle and the properties of angles in a circle. This includes the formula for the circumference of a circle, the radius of a circle, the area of a circle, and the central angle of a circle. This section also includes the definitions of interior and exterior angles of a circle and their measurements.

The second part of the worksheet focuses on the formulas for calculating angles in a circle. This includes the formula for the area of a sector, the formula for the arc length of a sector, and the formula for the central angle of a sector. This section also explains the formula for the area of a regular polygon and the formula for the area of a sector.

The third part of the worksheet focuses on the application of angles in a circle. This includes the formula for the angle between two intersecting lines, the formula for the area of a triangle, and the formula for the area of a parallelogram. This section also includes the formulas for the area of a regular polygon and the formula for the area of a sector.

The fourth part of the worksheet covers the application of angles in a circle in the context of other topics. This includes the formulas for the area of a circle and the area of an ellipse. This section also explains the formula for the perimeter of a triangle and the formula for the perimeter of a parallelogram. Finally, this section explains the formulas for the area of an irregular polygon and the formula for the area of a sector.

The analyzing angles in a circle worksheet is a comprehensive overview of the formulas and applications of angles in a circle. It covers a variety of topics such as the definition of a circle, the properties of angles in a circle, and the formulas for calculating angles in a circle. Through this worksheet, students will gain a better understanding of the fundamentals of angles in a circle and how to apply them in various contexts.

Conclusion

The Angles in a Circle Worksheet is a great tool for helping students understand the concept of angles and how they interact in a circle. It provides an interactive way to explore the properties of angles and circles, and is a great resource for both teachers and students alike. By using this worksheet, students can gain a better understanding of angles, which can be applied to a variety of different mathematical problems.

[addtoany]