Exploring Piecewise Functions: Algebraic and Graphical Approaches

Piecewise functions are a type of mathematical functions that are composed of multiple functions joined together at specific points. These functions are often used in calculus to find the derivative of a function, to solve equations, and to plot curves. By exploring piecewise functions both algebraically and graphically, we can gain insight into how they work and how to use them effectively.

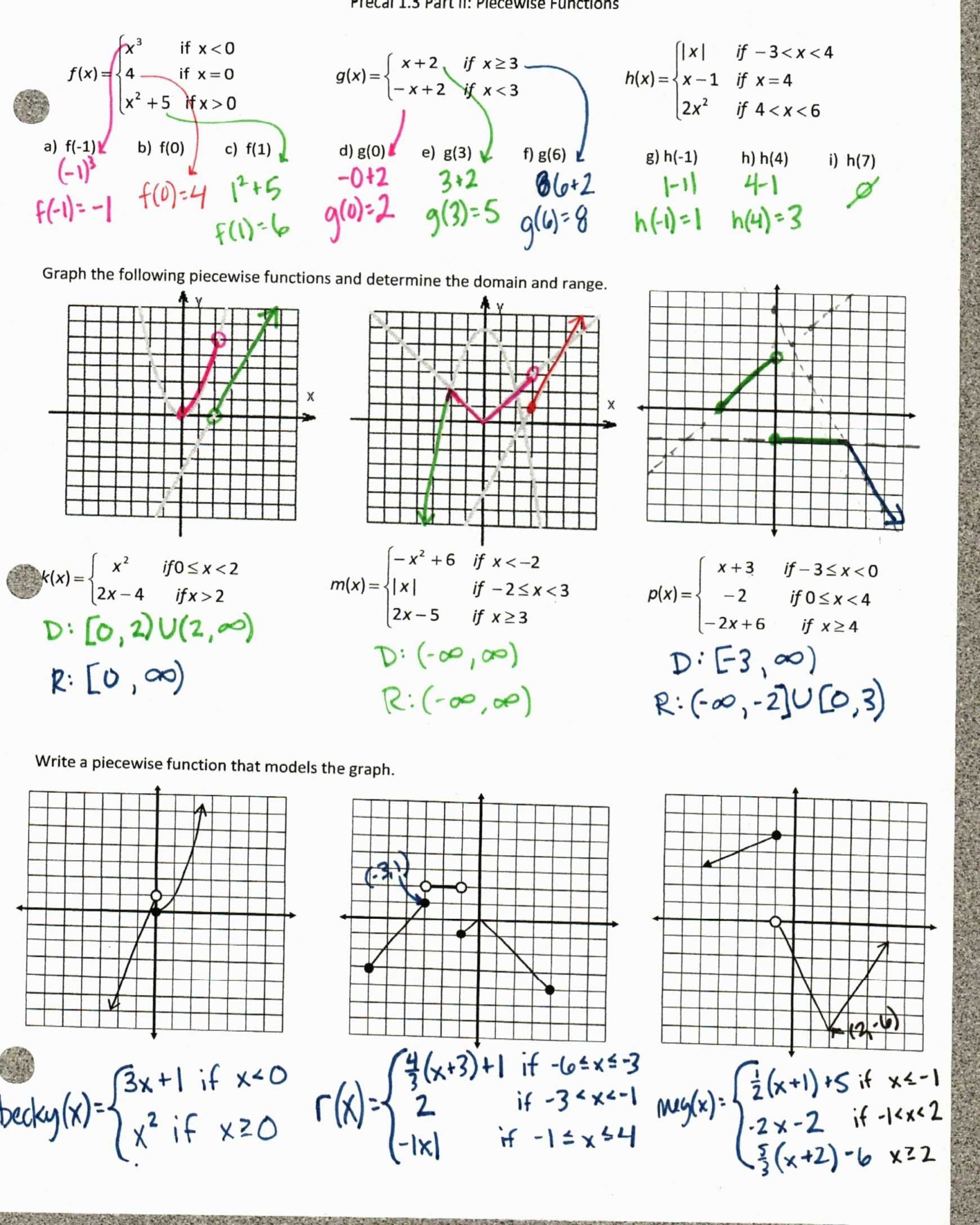
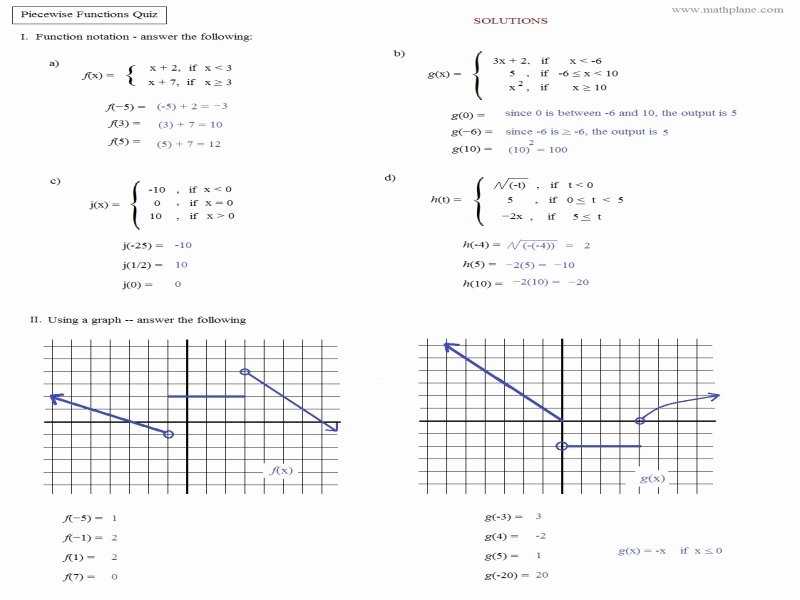
When exploring piecewise functions algebraically, we must first identify the specific boundaries of each function and then determine the function values at those points. To do this, we can use the algebraic definition of a piecewise function: a function that is expressed as a combination of two or more functions over distinct intervals of the domain. For each interval, we must determine the function value, which is typically expressed as an equation. These equations can then be graphed to visualize the piecewise function.

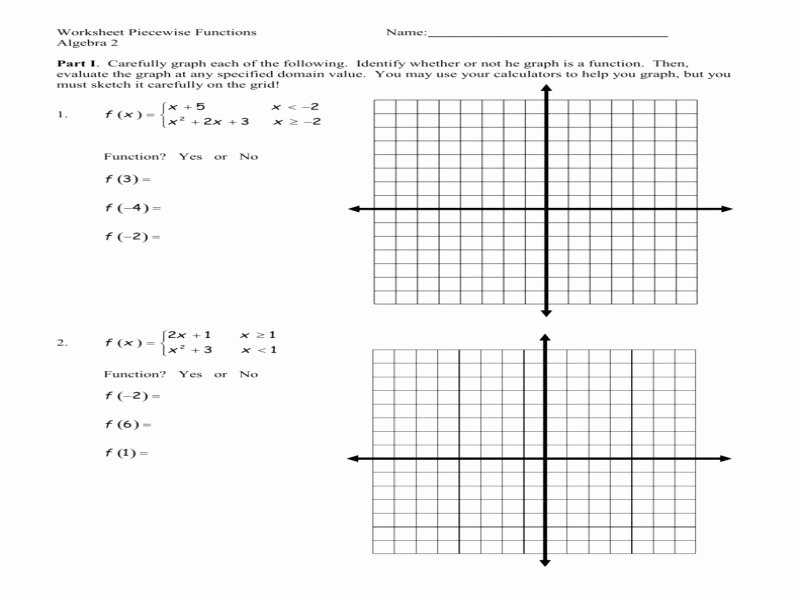
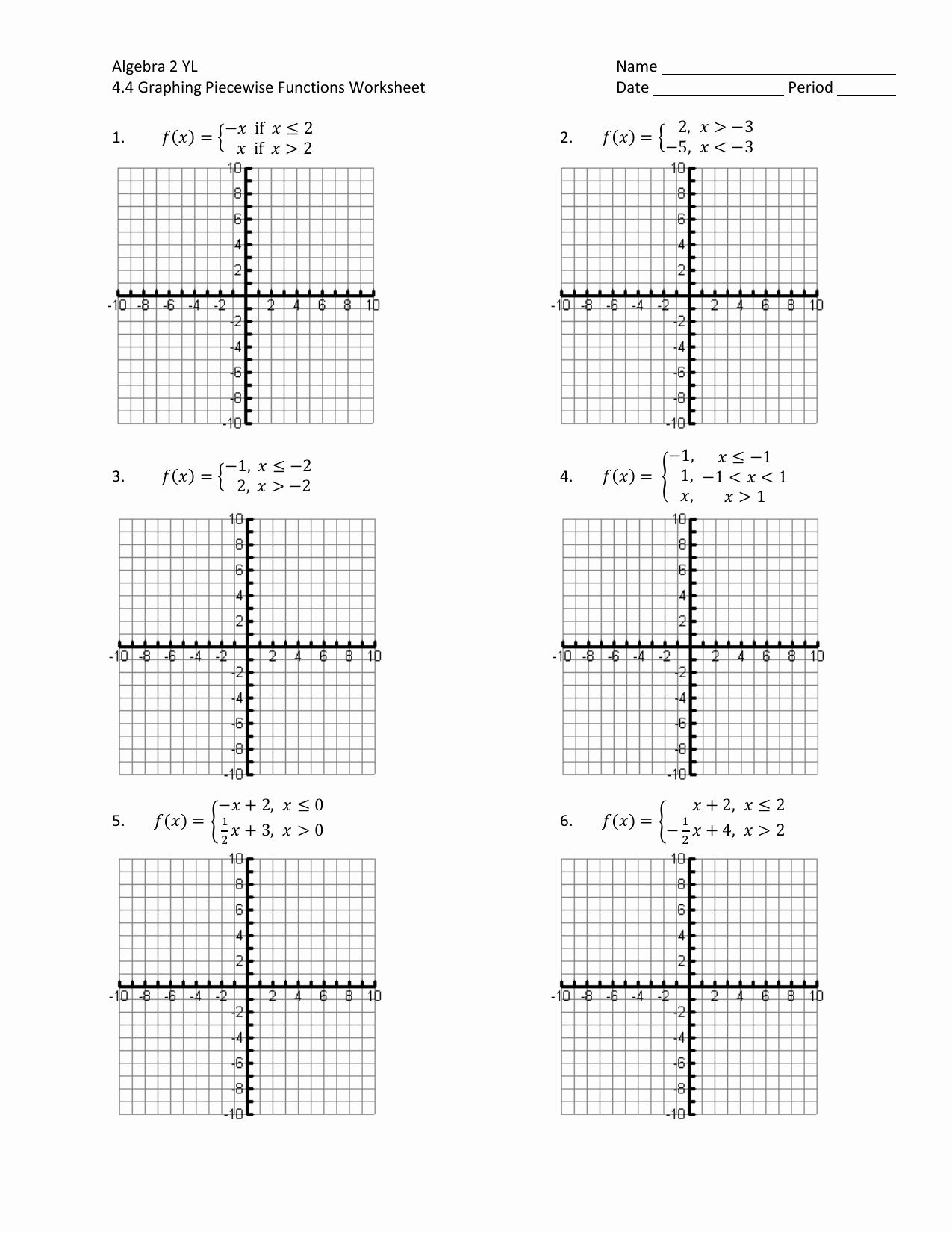
Graphing piecewise functions is a useful tool for understanding their behavior. A graph of a piecewise function can be characterized by the different segments that make up the function. Each segment is determined by the boundaries of the associated function and the graph of the function is created by connecting the points that correspond to the boundaries. As we move along the graph, we can see how the function changes according to its different components.

By exploring piecewise functions algebraically and graphically, we can gain a better understanding of their behavior and how to use them in our work. Whether we are using them to solve equations, find the derivative of a function, or plot curves, exploring piecewise functions gives us the necessary insight to use them effectively.

An Introduction to Piecewise Functions: Understanding the Basics of Algebra 2

Piecewise functions are a type of algebraic expression that allow for different mathematical calculations to be applied to different input values. These functions are often used to represent complex problems, such as economic models or engineering applications. They are also used in computer programming to create more efficient algorithms. In this article, we will discuss the basics of piecewise functions, including the definition, notation, and uses.

A piecewise function is an expression that is divided into multiple pieces, each piece representing a different mathematical operation. Each “piece” of the expression is a separate equation, and the input value determines which equation should be used. For example, a piecewise function might look like this:

f(x) =
\begin{cases}
2x+1 & \text{if } x < 0 \\ 3x-1 & \text{if } x \geq 0 \end{cases} In this example, the function is saying that if the input value (x) is less than 0, the output should be 2x+1. If the input value is greater than or equal to 0, the output should be 3x-1. Thus, the piecewise function can be thought of as two separate equations, one for each piece. The notation used in piecewise functions is similar to the notation used in other algebraic expressions. For example, the “if” statement used in the example above is written as “x < 0” and “x ≥ 0”. This notation is used to indicate which equation should be used for each input value. Piecewise functions are often used in engineering and economic applications. They are also used in computer programming to create more efficient algorithms. For example, a piecewise function may be used to solve a complex equation or to represent a large data set. By breaking the problem into pieces, it is easier to solve or analyze the data. In conclusion, piecewise functions are a type of algebraic expression that can be used to represent complex problems or data sets. They are divided into pieces, each piece representing a different mathematical operation. The notation used in piecewise functions is similar to the notation used in other algebraic expressions. Piecewise functions are often used in engineering, economics, and computer programming applications.

Utilizing Piecewise Functions to Solve Complex Algebra 2 Problems

Piecewise functions are powerful tools used to solve complex algebraic problems. A piecewise function is a function that is defined over a set of intervals, each of which can be assigned a different mathematical expression. In other words, a piecewise function is a function that is composed of multiple pieces each of which is defined by its own function.

Piecewise functions are used to solve complex algebraic problems because they allow for the expression of a wide range of values. By breaking a single expression into multiple pieces, different expressions can be applied to different parts of the domain, allowing for more precise calculations. For example, in an equation with multiple variables, a piecewise function can be used to assign different values to different domains of the equation, resulting in a more accurate solution.

Piecewise functions can also be used to solve problems involving discontinuous functions. For instance, a function may contain a discontinuous point, where the value of the function jumps from one point to another without any continuity. By breaking the function into multiple pieces, each containing a continuous function, it is possible to accurately calculate the value of the discontinuous point.

Piecewise functions are also useful in solving problems involving exponential or logarithmic functions. In such cases, a piecewise function can be used to assign different expressions to different parts of the domain, allowing for a more precise solution.

Piecewise functions are powerful tools used to solve complex algebraic problems. By breaking a single expression into multiple pieces, each containing its own function, it is possible to accurately calculate the value of any point in the domain. This makes them an invaluable tool in many areas of mathematics, such as calculus and linear algebra.

Conclusion

The worksheet on Piecewise Functions Algebra 2 provides a great introduction to the concept of piecewise functions. It provides examples of different types of piecewise functions, as well as practice problems which allow students to apply the concepts they have learned. By working through the worksheet, students will gain a better understanding of the concept of piecewise functions and how they can be used to solve problems.