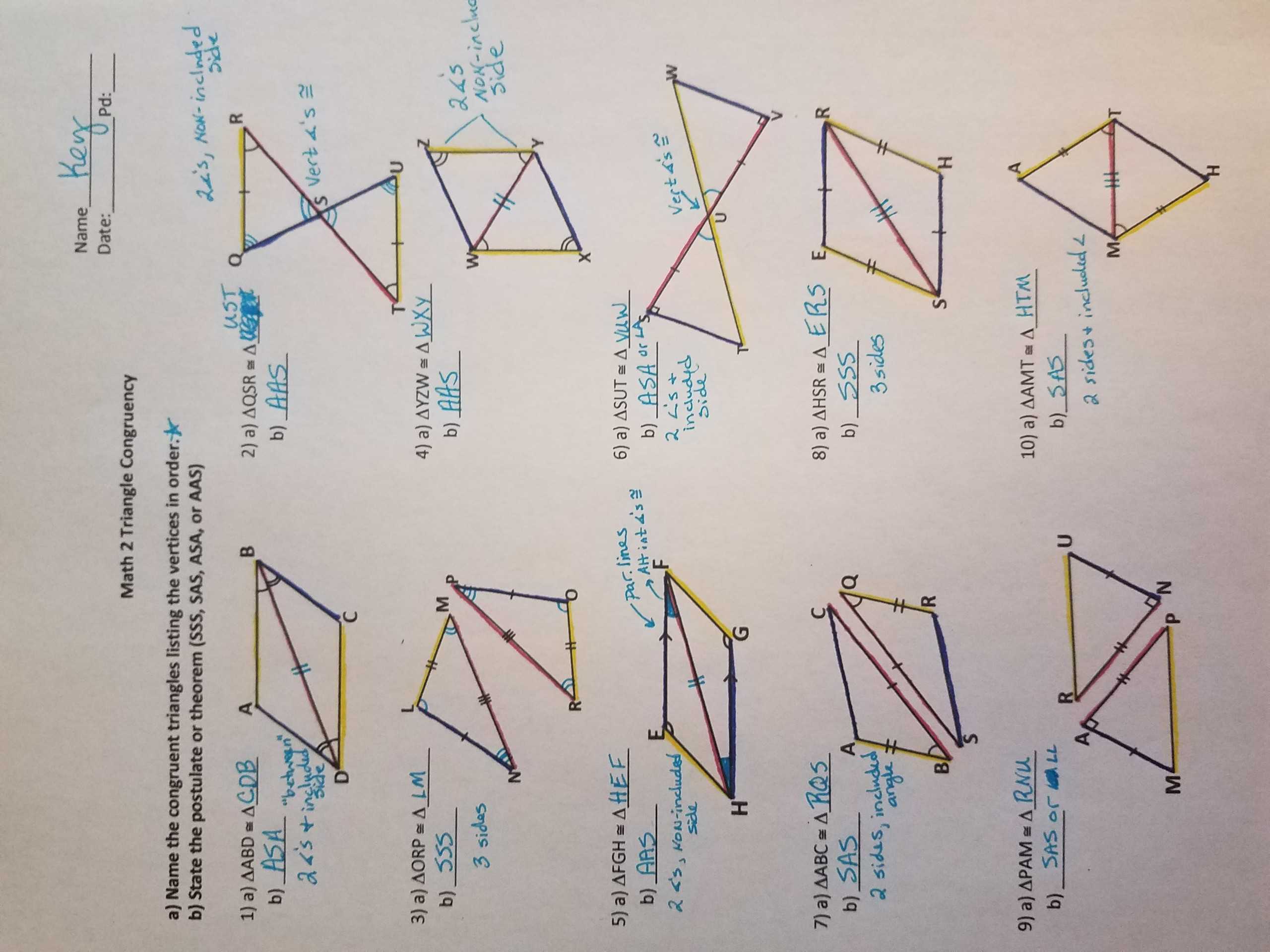
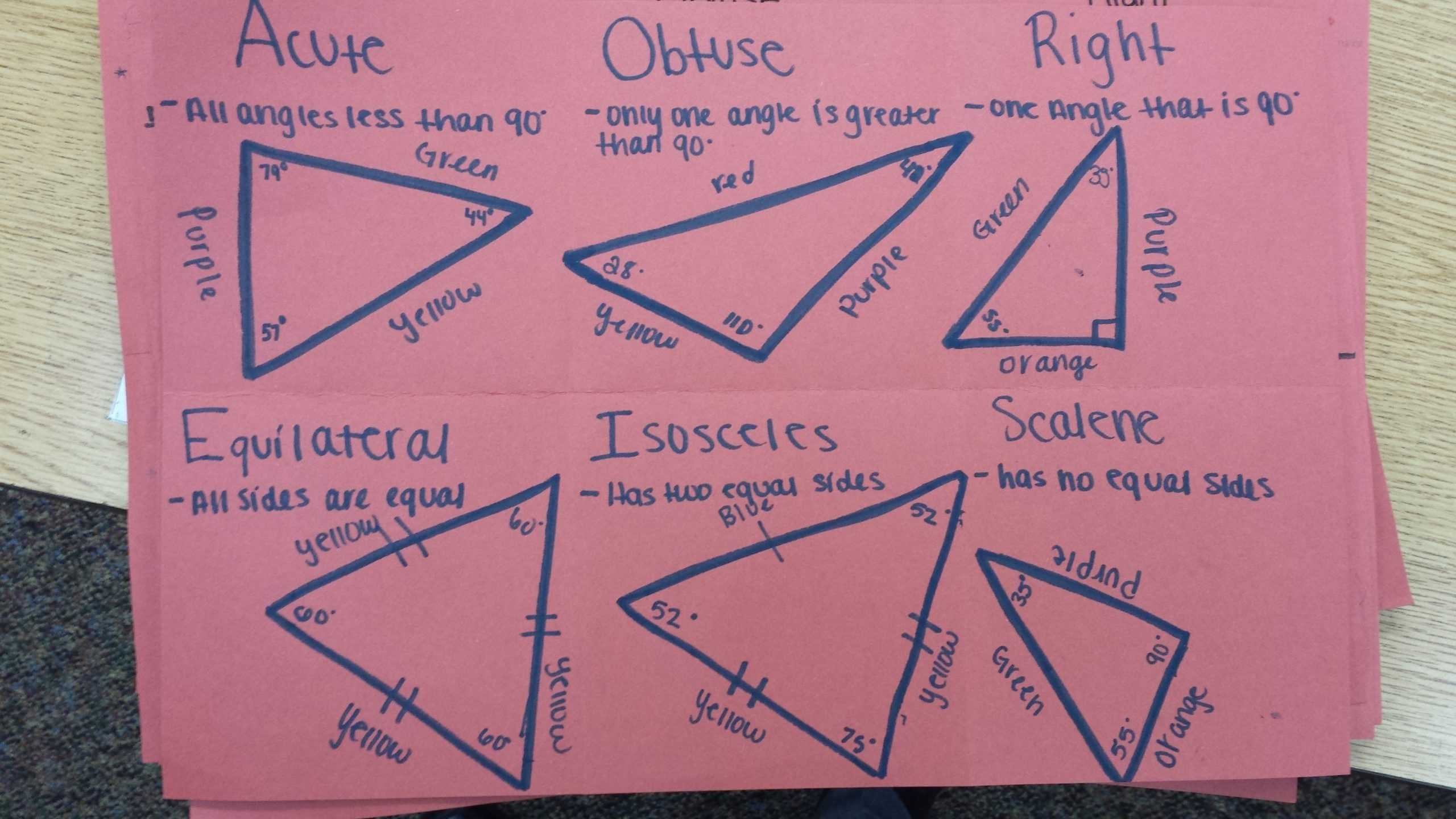
Exploring Triangle Proofs: A Step-by-Step Guide to Solving Triangle Proofs Worksheet Answers
1. Identify the triangle.
The first step to solving a triangle proof is to identify the triangle. Look for any given information about the triangle in the statement. This may include the side lengths, the angles, or any other information that helps you identify the triangle.
2. Determine the goal of the proof.
[toc]
The goal of a triangle proof is to prove a specific statement. This statement is usually related to the sides and angles of the triangle. Carefully read the statement to understand what needs to be proven.
3. Gather necessary tools.
Once the goal of the proof is determined, it is important to gather the necessary tools to prove the statement. These may include theorems, definitions, postulates, and other facts related to triangles.
4. Create a plan of attack.
With the goal of the proof in mind, it is important to create a plan of attack. This means breaking down the proof into smaller steps that can be tackled one by one. This will make it easier to understand the proof and create a logical flow of ideas.
5. Begin the proof.
Once the plan of attack is established, it is time to begin the proof. Begin by stating the given information and the goal of the proof. Then, use the tools gathered to logically prove each step of the proof.
6. Double check the proof.
When the proof is finished, double check each step to make sure it is valid and accurate. Make sure that each step logically follows the last and that all facts are used correctly.
7. Review the proof.
Finally, review the proof as a whole and make sure that it logically supports the stated goal. If any steps need to be changed or clarified, make the necessary changes and then review the proof again. Once the proof is complete and logically sound, it can be submitted for evaluation.
Practical Tips for Making Sense of Triangle Proofs Worksheet Answers
1. Understand the structure of the proof. Before attempting to solve a triangle proof, it is important to understand the structure of the proof. This includes identifying the given information and the goal of the proof. Additionally, it is important to note the steps that will be necessary to reach the goal of the proof.
2. Make sure all the given information is understood. Before attempting to solve a triangle proof, it is important to make sure all the given information is understood. This includes taking the time to read and understand each statement and identify any possible relationships between the statements.
3. Use diagrams to illustrate the problem. When attempting to solve a triangle proof, it can be helpful to draw a diagram to illustrate the problem. This can help to visualize the problem and make the proof easier to solve.
4. Identify the appropriate postulates, theorems, and definitions. When attempting to solve a triangle proof, it is important to identify the appropriate postulates, theorems, and definitions that can be used to prove the given statement.
5. Write out the proof. After identifying the necessary postulates, theorems, and definitions, it is important to write out the proof. This can help to ensure that each step of the proof is clear and that all the given information is accounted for.
6. Check the proof for accuracy. After writing out the proof, it is important to check the proof for accuracy. This includes checking the proof for any logical errors, such as incorrect assumptions or incorrect conclusions.
A Comprehensive Overview of Advanced Triangle Proofs Worksheet Answers
Advanced triangle proofs worksheet answers provide a comprehensive overview of the principles and methods of geometric proofs involving triangles. Triangle proofs are a fundamental part of geometry and have been used for centuries to prove various geometric propositions. Triangle proofs involve using the angles and sides of a triangle to prove a certain result.
The worksheet answers provided in an advanced triangle proof worksheet provide a step-by-step approach to solving triangle proofs. The worksheet begins by introducing the necessary notation and terminology associated with triangle proofs. This includes introducing the properties of angles and sides of a triangle, such as the Angle Sum Theorem and the Triangle Inequality Theorem. The worksheet then proceeds to introduce some of the most commonly used triangle proofs, such as the Law of Sines and the Law of Cosines.
The worksheet then explains how to set up a proof involving triangles, including how to set up the equations for the proof. This includes how to use the Triangle Inequality Theorem to determine the values of the angles and sides of the triangle. The worksheet then provides an example of a triangle proof to better illustrate the concepts explained in the worksheet.
Finally, the worksheet answers provide some practice problems to help reinforce the concepts presented in the worksheet. These practice problems can be used to test the student’s understanding of triangle proofs and the concepts associated with them.
An advanced triangle proof worksheet answers provide a comprehensive overview of the principles and methods of triangle proofs. The worksheet explains the notation and terminology associated with triangle proofs and provides step-by-step instructions on how to set up a proof involving triangles. It also provides example problems to help students practice the concepts presented in the worksheet. The practice problems are designed to help students better understand the principles and methods of triangle proofs.
Conclusion
The Triangle Proofs Worksheet Answers provide an effective way of understanding how to prove theorems involving triangles. Through careful analysis of the given data, students can develop an understanding of the different relationships between the three sides of the triangle and the angles of the triangle. This understanding can then be applied to more complex proofs, such as those involving more than three triangles. Ultimately, the Triangle Proofs Worksheet Answers provide a useful tool to help students understand the underlying principles of geometry.
[addtoany]