How Understanding Triangle Congruence Can Help Students Improve Their Problem-Solving Skills

Triangle congruence is a concept that can be used to improve students’ problem-solving skills. It is a fundamental topic in geometry, and understanding it is essential for students to be able to solve various types of problems related to triangles, such as determining the area of a triangle or finding the angle measurements of a triangle. Knowing about triangle congruence can help students identify and define the properties of a triangle and use them to solve problems.

First, understanding triangle congruence can help students better comprehend geometry problems that involve triangles. Students are often asked to identify the properties of a triangle, such as its angles and sides, or to calculate its area or perimeter. By recognizing the conditions of congruence between two triangles, students can quickly identify them and use them to solve the problem. For example, if two triangles are congruent, then the angles and sides of both triangles are equal in length. This can be used to calculate the area or perimeter of the triangle.

Second, triangle congruence can help students understand the concept of similarity. Although similar triangles have the same angles, they may not have the same side lengths. Knowing about triangle congruence can help students recognize when two triangles are similar and use this information to solve problems. For instance, if two triangles are similar, then the ratio of the lengths of corresponding sides of the two triangles is equal. This can be used to calculate the dimensions of one triangle if the dimensions of the other triangle are known.

Finally, triangle congruence can help students develop their problem-solving skills. By understanding what conditions must be met for two triangles to be congruent and similar, students can use this knowledge to identify the properties of the triangles in a problem and use them to solve the problem. This helps students develop their skills in recognizing patterns and using them to solve problems.

In conclusion, understanding triangle congruence can help students improve their problem-solving skills. By recognizing the conditions of congruence between two triangles, students can quickly identify them and use them to solve problems. It can also help students understand the concept of similarity, and use this knowledge to calculate the dimensions of one triangle if the dimensions of the other triangle are known. Finally, it can help students develop their skills in recognizing patterns and using them to solve problems. Understanding triangle congruence can be a valuable tool for students to improve their problem-solving skills.

Exploring the Various Types of Triangle Congruence Worksheet Answers

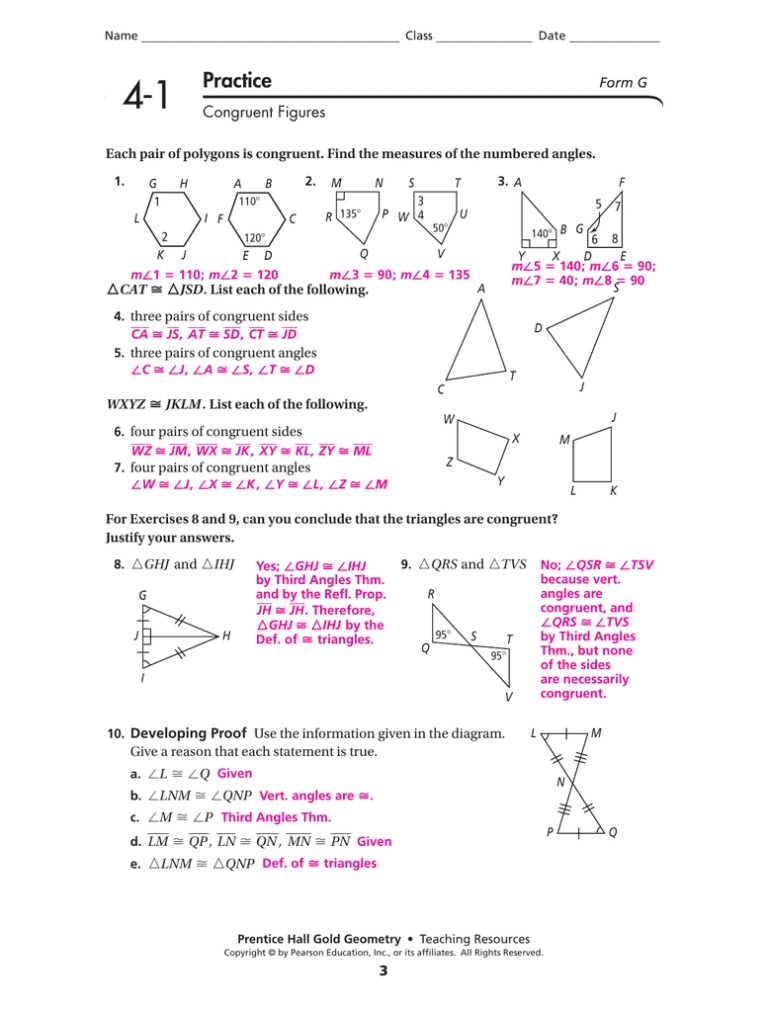
The Triangle Congruence Worksheet Answers are an excellent resource for students to learn the various methods of triangle congruence. Through this worksheet, students can explore the various types of triangle congruence, such as SSS, SAS, ASA, and RHS congruence.

SSS (Side-Side-Side) Congruence is the most basic form of triangle congruence. It states that if three sides of two triangles are equal in length, then the two triangles are congruent. This is often represented as “SSS”.

SAS (Side-Angle-Side) Congruence is more complex than SSS congruence in that it requires two additional conditions to be met. It states that if two sides of one triangle are equal in length to two sides of another triangle, and the included angle between the two sides is also equal, then the triangles are congruent. This is often represented as “SAS”.

ASA (Angle-Side-Angle) Congruence is similar to SAS congruence, but requires three conditions to be met instead of two. It states that if two angles of one triangle are equal in measure to two angles of another triangle, and the included side between the two angles is also equal, then the triangles are congruent. This is often represented as “ASA”.

RHS (Right-Angle-Hypotenuse-Side) Congruence is the most complex form of triangle congruence. It states that if the hypotenuse and a side of one right triangle are equal in length to the hypotenuse and a side of another right triangle, then the triangles are congruent. This is often represented as “RHS”.

Through the Triangle Congruence Worksheet Answers, students can explore each of the various types of triangle congruence and gain a greater understanding of the mathematics and principles behind them.

Analyzing Triangle Congruence Worksheet Answers to Assess Student Understanding of Geometry Concepts

This worksheet provides an opportunity to assess student understanding of the important geometry concept of triangle congruence. The worksheet contains questions that require students to identify the type of congruence in a given triangle, determine if two triangles are congruent, and identify the postulate used to prove two triangles are congruent.

Answers to the worksheet questions can be used to assess student understanding of congruence and their ability to identify which postulates, theorems and/or corollaries can be used to prove congruence. If a student can accurately answer the questions, it can be inferred that the student has a solid understanding of the concept.

Incorrect answers can be used to identify a student’s areas of misunderstanding. For example, if a student incorrectly identifies the type of congruence in a triangle, it could indicate that the student needs further instruction on the different types of congruence. Similarly, if a student incorrectly states that two triangles are congruent, it could signify a lack of understanding of the postulates and theorems used to prove congruence.

By analyzing the answers to the questions on the triangle congruence worksheet, teachers can identify where students are struggling with the material and can use this information to provide targeted instruction to ensure their understanding of the concept.

Conclusion

In conclusion, Triangle Congruence Worksheet Answers can be a great tool for students to practice their skills with triangle congruence and provide a helpful review of the material. With proper practice and guidance, students can ensure they understand and can apply the concepts of triangle congruence in the future.