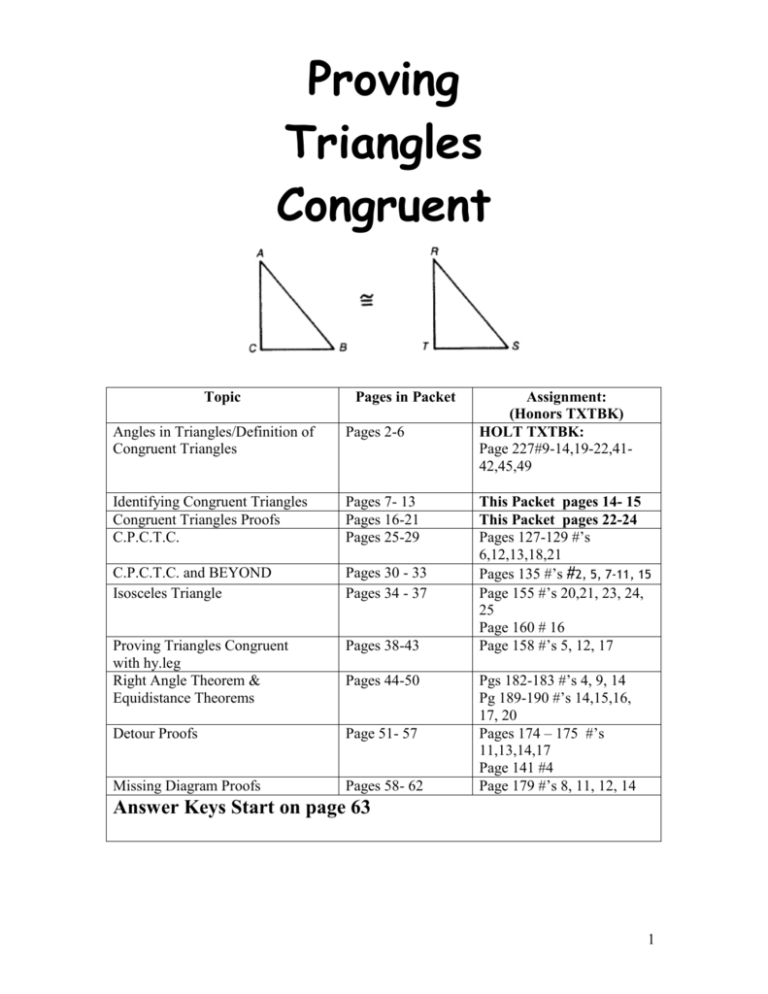
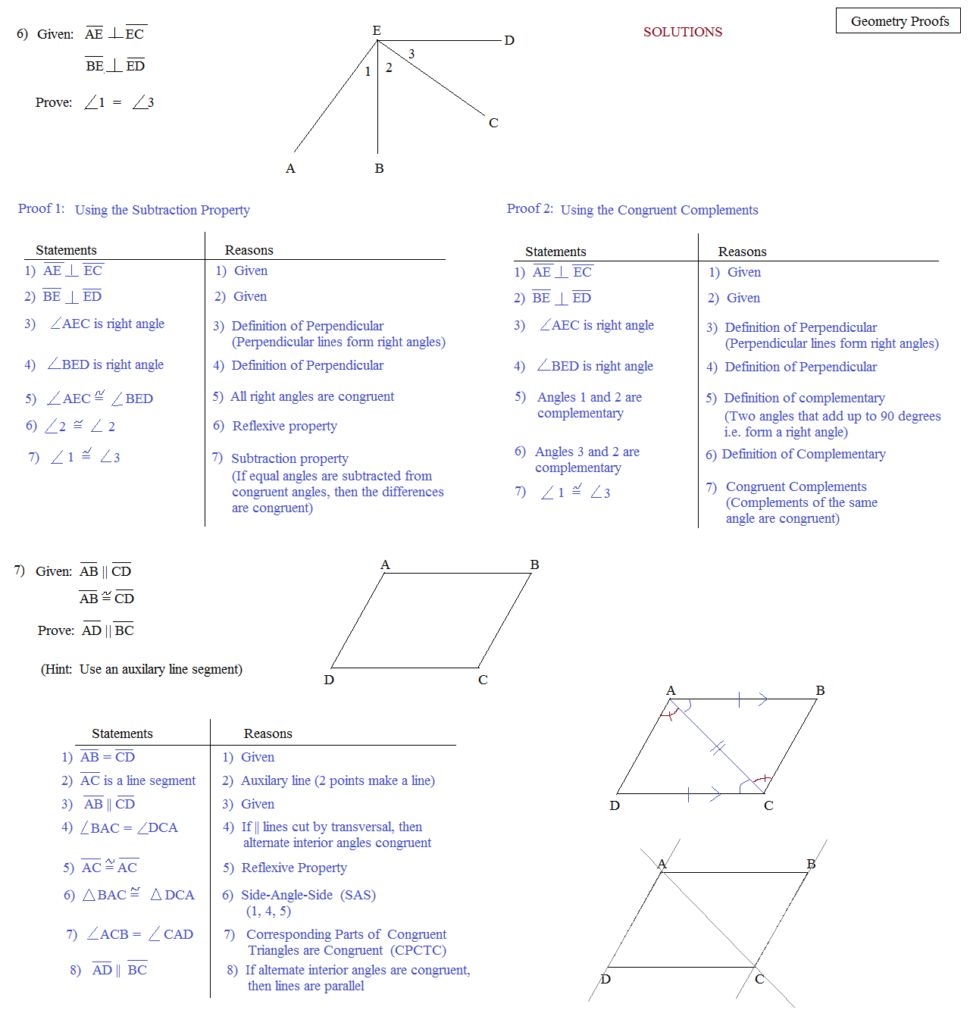
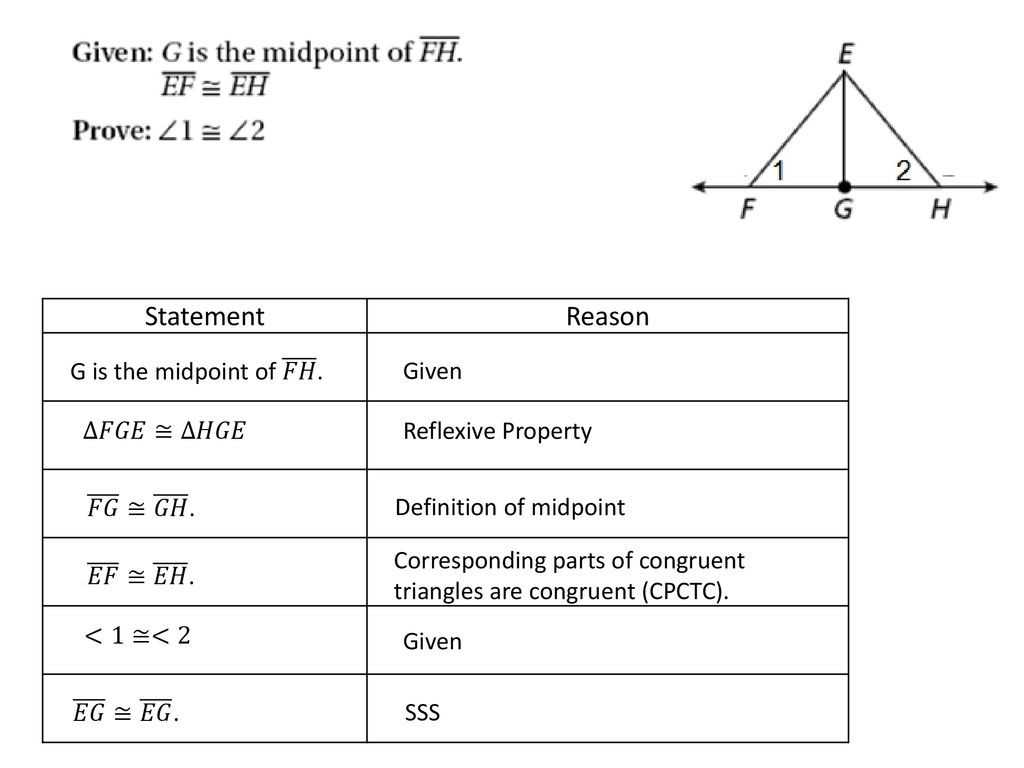
Exploring Triangle Congruence Proofs: An Introduction to the Basics

Triangle congruence proofs are a fundamental part of geometry, as they show how two triangles are the same shape and size. Such proofs essentially demonstrate that two triangles are similar or congruent, and are thus used to prove various theorems and properties.

In order to prove triangle congruence, a variety of methods may be employed. The most common include the Side-Side-Side (SSS), Side-Angle-Side (SAS), Angle-Side-Angle (ASA), and Angle-Angle-Side (AAS) postulates. Each of these postulates provides a specific set of conditions which, when met, confirm the congruence of two triangles.

The SSS postulate states that if all three sides of one triangle are congruent to the corresponding sides of another, then the two triangles are congruent. The SAS postulate states that if two sides and the included angle of one triangle are congruent to the corresponding sides and angle of another, then the two triangles are congruent. The ASA postulate states that if two angles and the included side of one triangle are congruent to the corresponding angles and side of another, then the two triangles are congruent. Finally, the AAS postulate states that if two angles and a non-included side of one triangle are congruent to the corresponding angles and side of another, then the two triangles are congruent.

It is important to note that triangle congruence proofs require a thorough understanding of triangle properties and theorems. Such knowledge is essential in order to establish the requisite conditions and demonstrate the congruence of two triangles.

In conclusion, triangle congruence proofs provide a basis for understanding the fundamental properties of triangles. By utilizing the four postulates, it is possible to prove that two triangles are congruent and thus gain a deeper insight into geometry.

Constructing Triangle Congruence Proofs Step-by-Step

Constructing triangle congruence proofs step-by-step is an important skill to master when studying geometry. Congruent triangles are triangles that have the same size and shape, and a proof can be used to demonstrate that they are congruent. By following a few steps, you can construct a valid triangle congruence proof.

The first step is to identify the congruence statement that you are trying to prove. This statement will tell you which triangles are congruent and should include the letters that label the triangles. For example, your congruence statement could be “Triangles ABC and DEF are congruent”.

The second step is to identify the given information. This can include information such as the lengths of sides or angles of the triangles. It is important to ensure that the information you include is relevant to the congruence statement you are trying to prove.

The third step is to draw a diagram of the triangles. This should include labels for all of the relevant angles and sides, as well as the congruence statement. It is crucial that the diagram be labeled accurately, as the proof will depend on the accuracy of the diagram.

The fourth step is to identify the postulates and theorems that can be used to prove the congruence statement. These postulates and theorems should be used to create a logical sequence of statements that will demonstrate the congruence of the triangles.

The fifth step is to list the steps of the proof. This should include a statement of the postulates and theorems that you are using, as well as any other supporting information. It is important to ensure that the steps of the proof are logical and that the congruence statement is proven.

The sixth and final step is to review the proof. This should include checking that all of the steps are logically connected and that the congruence statement is proven.

By following these steps, you can construct a valid triangle congruence proof. It is important to pay close attention to detail when constructing a proof, as any inaccuracies or logical errors may invalidate the proof. With practice, you will be able to construct triangle congruence proofs with confidence.

Identifying Common Errors When Constructing Triangle Congruence Proofs

Constructing a proof for triangle congruence is a complex task that requires careful consideration. Errors can easily be made in the process, leading to incorrect conclusions. Some of the most common errors when constructing a triangle congruence proof include:

1. Misinterpreting the given information: In order to construct an accurate proof, it is essential to carefully analyze the given information and properly interpret what it is saying. Misinterpreting the given information can result in an incorrect conclusion.

2. Making assumptions without sufficient justification: It is important to remember that assumptions should not be made without sufficient justification. It is essential to provide logical reasoning and evidence to support any assumptions in the proof.

3. Neglecting to use the properties of congruent triangles: Congruent triangles have many properties that can be used to make deductions. If these properties are not used, then deductions will be made incorrectly.

4. Neglecting to consider the order of statements: When constructing a triangle congruence proof, it is important to consider the order of statements. If the statements are in the wrong order, then the proof may be incomplete or incorrect.

5. Neglecting to state the conclusion: At the end of the proof, a conclusion should be stated. Neglecting to do so will result in an incomplete proof.

These are some of the most common errors when constructing a triangle congruence proof. It is important to be aware of these errors in order to create an accurate and complete proof.

Analyzing Triangle Congruence Proofs: Tips for Finding Solutions Faster

When faced with a triangle congruence proof, it can be difficult to know where to start and how to go about finding a solution. However, there are some tips that can help you to analyze proofs more quickly and accurately.

First and foremost, it is important to read the proof thoroughly. Make sure to pay attention to each of the given statements and the relationships between them. This will help you to determine what information is true and what may need to be proven.

Second, draw the provided diagram and label it properly. This will allow you to visualize the proof and make it easier to solve.

Third, identify the main goal of the proof. This will help you to determine what statement needs to be proven and which lemmas should be used.

Fourth, use the given statements to construct a logical argument. This will help you to determine which lemmas should be applied in order to reach the desired conclusion.

Finally, double-check your work and make sure that each step of your argument is valid. This will help to ensure that your proof is sound and that the desired result is achieved.

By following these tips for analyzing triangle congruence proofs, you will be able to find solutions more quickly and accurately. With practice, you will be able to master this process and be well on your way to becoming an expert in triangle congruence proofs.

Leveraging Triangle Congruence Proofs to Teach Geometry Concepts

Triangle congruence proofs are an excellent way to teach geometry concepts in the classroom. By utilizing triangle congruence proofs, students can develop a comprehensive understanding of triangle properties and geometry fundamentals.

Triangle congruence proofs allow students to explore the different properties of triangles and practice applying them to real-world problems. In a triangle congruence proof, students must use logical reasoning to identify the corresponding parts of two triangles in order to establish their congruence. This type of proof requires students to pay close attention to the properties of the triangles, such as the angles, side lengths, and other characteristics. Through this process, students can practice their problem solving skills and gain a better understanding of how geometry can be used to solve real-world problems.

In addition to problem solving, triangle congruence proofs also help students develop their critical thinking skills. By analyzing the properties of two triangles, students must make informed decisions about how to best demonstrate their congruence. This requires students to think beyond the surface level and consider the smaller details of the problem.

Finally, triangle congruence proofs can also help students develop an appreciation for the beauty of geometry. By exploring the properties of triangles and discovering the relationships between them, students can gain an understanding of why geometry is so important. This appreciation can lead to an increased interest in the subject and can help students gain a better understanding of the practical applications of geometry.

Overall, triangle congruence proofs are an excellent tool for teaching geometry concepts in the classroom. By utilizing triangle congruence proofs, students can gain a comprehensive understanding of triangle properties and geometry fundamentals, practice their problem solving and critical thinking skills, and develop an appreciation for the beauty of geometry.

Understanding the Benefits of Using Triangle Congruence Proofs for Problem Solving

Triangle congruence proofs are powerful tools used to solve various types of problems related to geometry. A congruence proof is a mathematical argument used to prove that two objects are the same size and shape. In the case of triangle congruence proofs, the objects in question are triangles.

Using triangle congruence proofs to solve problems requires an understanding of the properties of triangle congruence and of the methods for proving triangle congruence. The properties of triangle congruence include the Side-Side-Side (SSS) Postulate, the Angle-Side-Angle (ASA) Postulate, and the Side-Angle-Side (SAS) Postulate. These postulates dictate the conditions that must be met for two triangles to be congruent. The methods for proving triangle congruence are based on these postulates and involve showing that the given figures satisfy the postulates.

The benefits of using triangle congruence proofs for problem solving are numerous. First, triangle congruence proofs provide a reliable way to determine whether or not two triangles are congruent. This allows for the accurate solution of problems involving triangles. Second, triangle congruence proofs allow for the identification of the relationships between the sides and angles of triangles. This can be used to solve problems that require the comparison of the ratios of side lengths and angles between two triangles. Finally, triangle congruence proofs can be used to prove theorems related to the properties of triangles.

In conclusion, triangle congruence proofs provide an effective and reliable way to solve various types of problems related to geometry. By understanding the properties of triangle congruence and the methods for proving triangle congruence, one can effectively utilize triangle congruence proofs for problem solving.

Crafting Effective Triangle Congruence Proofs Strategies

Writing a triangle congruence proof can be a challenging task, but with the right strategies, it can be done effectively. First, it is important to properly identify the given information in the problem. Pay careful attention to any congruent triangles that are mentioned, as well as any other given information such as side lengths, angle measurements, or other triangle properties.

Once the given information has been identified, the next step is to determine a plan of attack. Consider what facts will be needed to prove the desired conclusion, and choose a path of reasoning that will lead to that conclusion. It is also important to consider how each step of the proof will be justified. Will a theorem be used, or will a triangle congruence postulate be applied?

Once a plan of attack has been determined, it is time to begin constructing the proof. Start with the given information and clearly state any relevant facts. As you progress through the proof, be sure to explain each step and provide appropriate justification. Be sure to keep track of any triangles that have been proven congruent and any properties that have been utilized.

Once all the necessary steps have been completed, draw a conclusion that states if the triangles are congruent or not, and why. Finally, review the proof to make sure all the steps are logically sound and that the conclusion follows from the evidence presented.

By following these strategies, writing an effective triangle congruence proof is possible. Careful attention should be paid to the given information, a plan of attack determined, and each step of the proof justified. With careful thought and consideration, a successful proof can be written.

Examining the Different Types of Triangle Congruence Proofs

Triangle congruence proofs are a method of demonstrating congruence between two triangles. In order to successfully prove that two triangles are congruent, there are several different types of proofs that can be used. These include side-side-side (SSS), side-angle-side (SAS), angle-side-angle (ASA), and angle-angle-side (AAS) proofs.

Side-side-side proofs demonstrate congruence by showing that all three sides of one triangle are equal to the corresponding sides of the other. This proof relies on the fact that if three sides of two triangles are equal, then the triangles are congruent. In order to prove congruence, it is necessary to show that the lengths of two pairs of sides are equal and that the third pair of sides is equal.

Side-angle-side proofs rely on the fact that if two sides and the included angle of one triangle are equal to the corresponding sides and the included angle of another triangle, then the triangles are congruent. In order to use this proof, it is necessary to show that two pairs of sides are equal and that the included angles are equal.

Angle-side-angle proofs rely on the fact that if two angles and the included side of one triangle are equal to the corresponding angles and the included side of another triangle, then the triangles are congruent. In order to use this proof, it is necessary to show that two pairs of angles are equal and that the included sides are equal.

Finally, angle-angle-side proofs rely on the fact that if two angles and a non-included side of one triangle are equal to the corresponding angles and non-included side of another triangle, then the triangles are congruent. In order to use this proof, it is necessary to show that two pairs of angles are equal and that the non-included sides are equal.

In conclusion, there are four different types of triangle congruence proofs: side-side-side, side-angle-side, angle-side-angle, and angle-angle-side. Each of these proofs relies on different conditions and requires different types of information in order to demonstrate congruence between two triangles.

Debunking the Myths Surrounding Triangle Congruence Proofs

Triangle congruence proofs are an important part of geometry, yet they can be daunting to many students. There are several common misconceptions that make them seem daunting, but these misconceptions are not valid. It is important to understand the truth behind these myths in order to be successful in proving triangle congruence.

The first myth is that triangle congruence proofs are incredibly difficult. This is not true. While they can be challenging, proper study and preparation can make them manageable. With practice, students can become adept at understanding and writing proofs.

The second myth is that there is only one way to prove triangle congruence. In fact, there are several different ways to prove triangle congruence. Depending on the particular problem, certain methods may be better suited than others. It is important to be familiar with the various methods and to understand when each should be used.

The third myth is that triangle congruence proofs are purely memorization-based. This is not true. While there are some facts and formulas that students must memorize, the proofs themselves require more than memorization. Students must be able to apply the facts and formulas to the particular problem and come up with a logical proof.

The fourth myth is that triangle congruence proofs can be solved without understanding the underlying concepts. This is false. Understanding the underlying concepts is essential to successfully proving triangle congruence. Without a proper understanding of the geometry behind triangle congruence, it is impossible to create a logical proof.

These myths can be dispelled with a little bit of knowledge and practice. Triangle congruence proofs are a challenging but manageable part of geometry. With the right preparation, students can be successful in understanding and writing proofs.

Creating Engaging and Informative Triangle Congruence Proofs Worksheets

Creating worksheets to help students understand triangle congruence proofs can be an effective tool for teaching and learning. This informative worksheet will guide students through the steps of creating and understanding triangle congruence proofs. It will provide students with the necessary tools to understand the fundamental principles of triangle congruence and how to apply them to their own proofs.

The worksheet will begin by introducing the basics of triangle congruence. This will include defining what a congruent triangle is and the associated terminology used in proving congruence. It will also provide a visual representation of the typical diagrams used in triangle congruence proofs.

Next, the worksheet will provide a step-by-step guide to creating a triangle congruence proof. It will list the steps in order, beginning with identifying the given information, then the conclusion that is being proven, followed by the statements and reasons used to prove the conclusion.

The worksheet will also provide examples of triangle congruence proofs for students to practice. These examples will be accompanied by a brief explanation of the proof and how it was completed.

Finally, the worksheet will provide a section for students to practice creating their own triangle congruence proofs. This will enable students to test their knowledge and understanding of the material and build confidence in their ability to create triangle congruence proofs.

This engaging and informative worksheet will provide students with the necessary tools to understand the fundamental principles of triangle congruence, and how to apply them to create their own proofs.

Conclusion

In conclusion, Triangle Congruence Proofs Worksheet is a great resource for students to use to practice their understanding of the principles of triangle congruence. By working through the worksheet, students can gain a better understanding of the rules and principles that govern triangle congruence and how to use them to solve problems. This worksheet also offers an opportunity for students to receive feedback on their answers, allowing them to make corrections and gain a deeper understanding of the material.