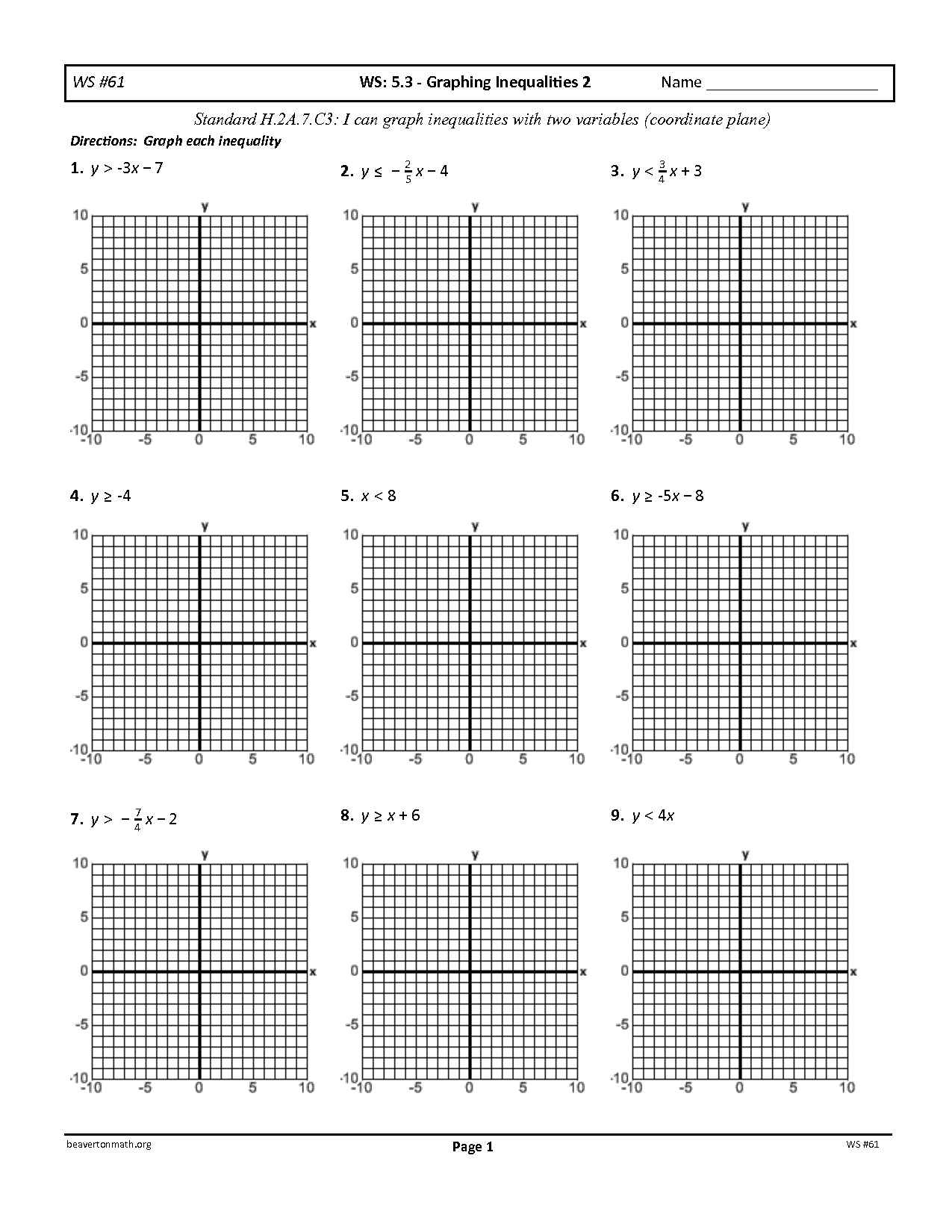
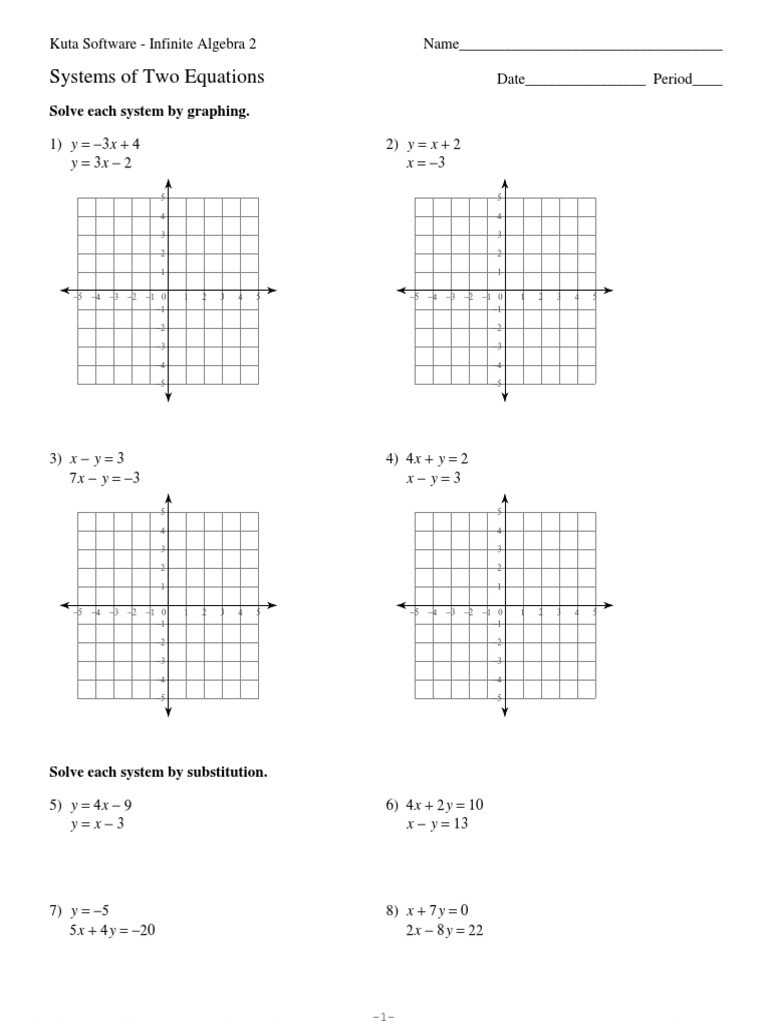
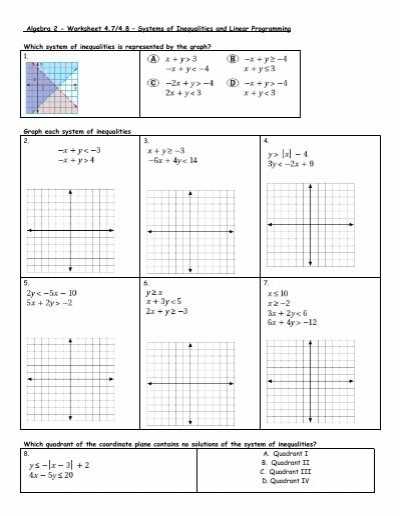
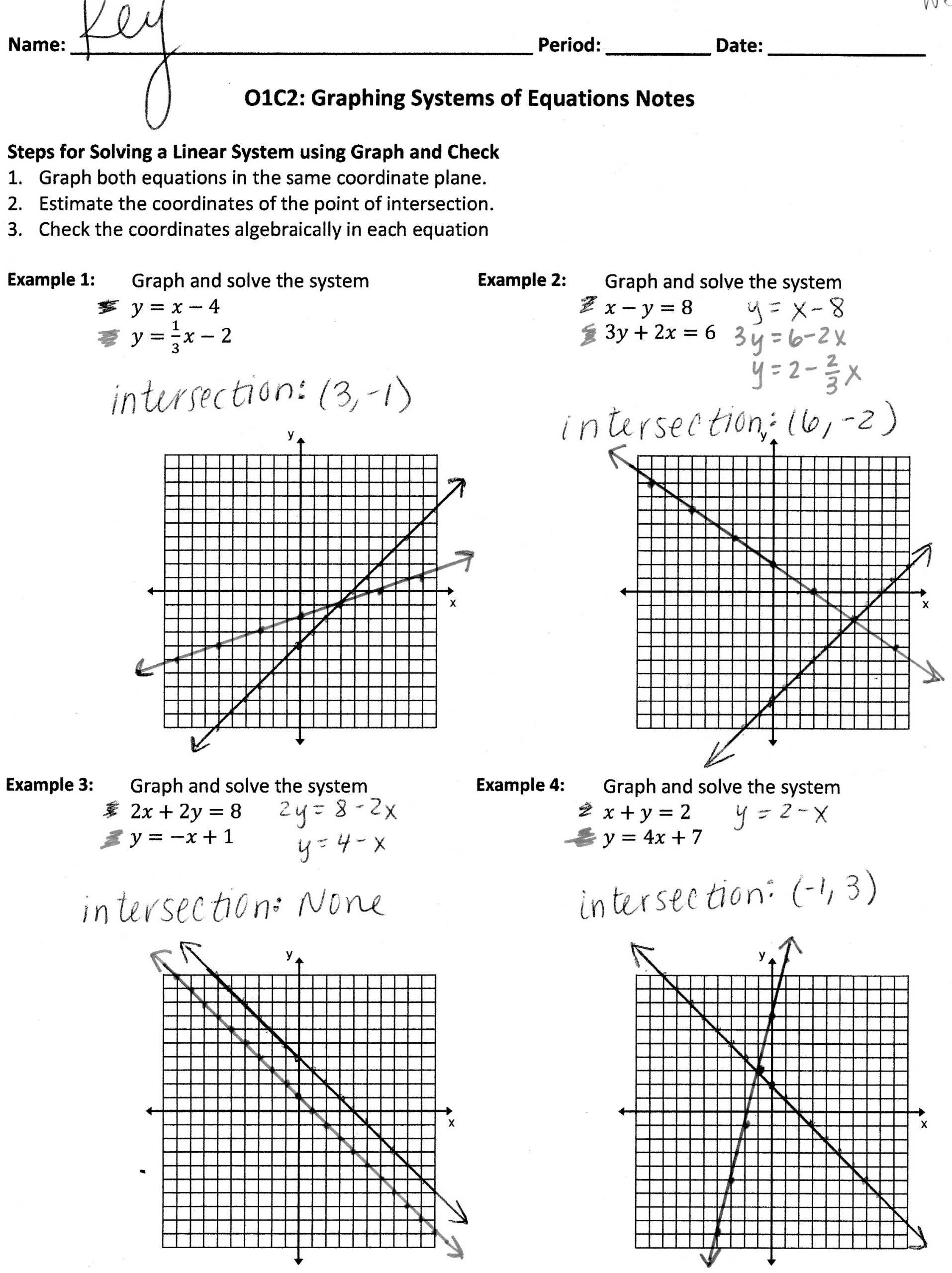
Exploring Systems of Inequalities: An Overview of the Worksheet

A system of inequalities is a set of equations or inequalities that describe a relationship between sets of variables. A worksheet is an effective way to help students explore systems of inequalities and gain an understanding of their solutions.

A worksheet typically consists of a series of problems related to systems of inequalities. The worksheet should introduce the main concepts related to systems of inequalities, such as the inequality symbols, the meaning of the symbols, and the types of solutions that can occur. It should also provide examples of inequalities and problem-solving strategies.

The worksheet should also provide practice problems for students to work through. These problems should include systems of linear inequalities, as well as more complex systems such as systems of quadratic or cubic inequalities. Examples of problems should include identifying the solutions to a system of inequalities, graphing the solutions, and determining the type of solution (i.e. if the solution is one point, two points, or an entire region).

In addition to providing practice problems, the worksheet should include an explanation of the solutions for each problem. This should include an explanation of how the inequalities are related, how the solutions were found, and why the solutions are the way they are. This explanation should allow students to gain an understanding of the underlying concepts related to systems of inequalities.

Finally, the worksheet should be designed to foster independent learning and critical thinking skills. It should provide open-ended questions to stimulate further exploration and encourage students to think outside the box. It should also provide opportunities for students to find creative solutions to systems of inequalities.

In summary, a worksheet is an effective way to explore systems of inequalities and help students gain an understanding of their solutions. It should introduce the main concepts, provide examples of problems, explain the solutions, and foster independent learning and critical thinking.

How to Use a Systems of Inequalities Worksheet to Solve Real-World Problems

A systems of inequalities worksheet can be used to solve real-world problems by providing a systematic approach for finding solutions. This worksheet can help to identify the range of values that satisfy a given set of constraints. It is useful for finding the maximum and minimum values of a function, the area of a region, and the solution to linear programming problems.

To use a systems of inequalities worksheet, start by defining the problem. Identify the variables and the constraints that apply to the problem. For each constraint, define an inequality that describes the relationship between the variables. Graph the inequalities on a coordinate plane and label each one. Next, identify the region that is shaded by the inequalities. This region will be the set of values that satisfies the constraints. Finally, calculate the maximum and minimum values of the function within the shaded region.

A systems of inequalities worksheet is a valuable tool for solving real-world problems. By using this worksheet, users can identify the range of values that satisfy a set of constraints and calculate the maximum and minimum values of a function. This worksheet can help to save time and make problem-solving more efficient.

Understanding Graphical Representations of Systems of Inequalities

Graphical representations of systems of inequalities are an important tool in mathematics. They can help to illustrate and analyze the relationships between sets of equations and inequalities. A system of inequalities is a set of two or more inequalities that have the same variables in them. Graphically, these can be represented by a set of lines or curves in a coordinate plane.

A line on a graph is an equation representing a set of points that all have the same x or y coordinate value. Inequality graphs involve two or more lines, and the area between them illustrates the solutions to the system of equations. The area that satisfies the given set of inequalities is typically shaded in, while the area that does not satisfy the inequalities is left unshaded.

The type of shading used to represent a system of inequalities is important. If the inequalities are all greater than or equal to (≥) or less than or equal to (≤), then the shaded area is typically below or above the curves, respectively. If the inequalities involve both greater than and less than and are not equal, then the shaded area is typically in between the curves.

Graphical representations of systems of inequalities help to illustrate the relationships between the sets of equations and inequalities, allowing us to quickly and easily visualize the solutions to the system. They are an important tool that can be used to gain a deeper understanding of sets of equations and inequalities.

Strategies for Solving Systems of Inequalities: A Step-by-Step Guide

Solving systems of inequalities is a common problem faced by mathematicians and problem solvers alike. This step-by-step guide will provide a general overview of the process and provide an outline of the steps required to solve a system of inequalities.

The first step in solving a system of inequalities is to identify the variables involved and the type of inequalities. Identifying the variables will help determine which types of methods can be used to solve the system. There are two main types of systems of inequalities: linear and nonlinear systems. Once the type of system is identified, the appropriate methods can be used.

Once the types of variables and the system type have been identified, the next step is to graph the inequalities. This will help visualize the solution to the system and can be used to check the accuracy of the solution.

The next step is to identify any regions of the graph which are not part of the solution set. This will help narrow down the solution set and lead to a more accurate answer. Any regions of the graph which do not meet the conditions set by the inequalities should be eliminated from the solution set.

Once the regions of the graph which are not part of the solution set have been identified, the next step is to identify the regions of the graph which do meet the conditions set by the inequalities. This will provide a clearer picture of the solution set and can be used to check the accuracy of the solution.

The last step is to solve for the variable to find the solution set. This can be done by using methods such as substitution, elimination, or graphing. Once the solution set is found, it can be checked for accuracy by comparing it to the graph obtained earlier.

By following these steps, solving systems of inequalities can be a relatively straightforward process. It is important to remember that the process may differ slightly depending on the type of system being solved and the methods used to solve it. However, by following this step-by-step guide, anyone can become a skilled problem solver when it comes to solving systems of inequalities.

Unlocking the Intersection of Systems of Inequalities Using the Worksheet

The Worksheet is a powerful tool for unlocking the intersection of systems of inequalities. It is a graphical representation of a system of equations that can be used to calculate the intersection of two or more inequalities. The Worksheet allows for the visualization of the intersection of two or more lines, and can be used to determine the range of values that satisfy the system of equations.

To use the Worksheet, the user must first enter the equations of the two or more lines into the worksheet. The equations should be written in the form of inequalities, such as y > x or y < x. Once the equations are entered, the user can then plot the lines on the worksheet. The intersection point of the lines will be marked by a solid circle, indicating the range of values that satisfy the system of inequalities. The user can also use the Worksheet to calculate the intersection of multiple lines by entering the equations of each line and then plotting them on the worksheet. The intersections of the lines will be marked with a solid circle, indicating the range of values that satisfy the system of equations. The user can also use the Worksheet to solve systems of inequalities by entering the equations of the lines into the Worksheet and then plotting them. The intersection point of the lines will be marked by a solid circle, indicating the range of values that satisfy the system of equations. The Worksheet is an invaluable tool for solving systems of inequalities and can be used to quickly and accurately determine the range of values that satisfy the system of equations. It provides a visual representation of the intersection of multiple lines, and can be used to quickly and easily calculate the intersection of two or more lines.

Working with Multiple Inequalities: Analyzing and Exploring the Solutions

Working with multiple inequalities can be a challenging but rewarding experience that can open up many possibilities. Generally, multiple inequalities involve several inequalities that have to be solved in order to find the solution. The first step in working with multiple inequalities is to identify the variables and the conditions that need to be satisfied. Once the variables and conditions have been identified, the next step is to graph the inequalities and explore the solutions within the graph.

The graph of the inequalities can be used to identify the regions in which the solutions are located. The lines that separate the different regions are identified as the boundaries and their intersection points identify the solutions. To further refine the solutions, the inequalities can be combined into a single equation and the solutions can be expressed in terms of the different variables.

If the solutions are not expressed as a single equation, they can be expressed as an interval. In this case, the boundaries of the solution can be expressed as a set of inequalities that need to be satisfied. This can be used to express the range of values that the solutions can take on.

Finally, the solutions can be checked to ensure that they do satisfy the original conditions. If the solutions do not satisfy the conditions, then additional work needs to be done to identify the correct solutions. Once the solutions are identified, they can be used to explore further possibilities.

Working with multiple inequalities can be both a mentally stimulating and rewarding experience. It requires careful analysis, problem solving skills and patience. By understanding the basics of multiple inequalities, one can explore many possibilities and come to interesting and unique solutions.

Using Systems of Inequalities to Explore Real-World Problems

Systems of inequalities are powerful tools for exploring and understanding real-world problems. These systems of equations, consisting of two or more linear inequalities, allow us to analyze the range of possible solutions to a given problem. By plotting the inequalities on a graph, we can visualize the region of all possible solutions, allowing us to gain insights into the problem at hand.

For example, consider a problem where we want to determine the region of feasible solutions for two different production processes. In this case, each production process has its own set of constraints which determine the range of viable solutions. We can represent these constraints using systems of inequalities. By plotting the inequalities on a graph, we can observe the region of feasible solutions and make informed decisions about which production process to use.

Systems of inequalities can also be used to analyze problems involving multiple resources. For instance, consider a situation where we need to determine the region of feasible solutions for a project involving multiple resources. This problem can be represented by a system of linear inequalities, where each inequality represents the constraints of one of the resources. By plotting the inequalities on a graph, we can observe the region of feasible solutions and make informed decisions about how to best utilize our resources.

In addition to analyzing problems involving multiple resources, systems of inequalities can be used to explore a variety of other real-world problems. For instance, they can be used to analyze problems involving budget constraints, labor force limitations, and environmental constraints. By plotting the inequalities on a graph, we can visualize the region of feasible solutions and gain valuable insights into the problem at hand.

Overall, systems of inequalities are a powerful tool for exploring and understanding real-world problems. By plotting the inequalities on a graph, we can visualize the region of feasible solutions, allowing us to make informed decisions about how to best utilize our resources. With this tool, we can gain valuable insights into a variety of real-world problems and make more informed decisions.

Analyzing the Solutions of Systems of Inequalities with the Worksheet

The worksheet provides a useful tool for analyzing the solutions of systems of inequalities. It is a simple, yet powerful tool that can be used to identify the points of intersection of two or more inequalities.

The worksheet begins by having the user enter the inequalities. For each inequality, the user must enter its slope and y-intercept. Then, the user must enter the coordinates for the two points of intersection. After the user has entered all of this information, the worksheet will calculate the solutions of the system of inequalities.

The worksheet will then display the solutions of the system of inequalities in the form of a graph. This graph will show the points of intersection of the inequalities. It will also indicate which points are solutions to the system of inequalities.

Once the user has identified the solutions to the system of inequalities, they can use the worksheet to analyze the solutions. For example, they can use the worksheet to find the area of the region that is bounded by the solutions. They can also use the worksheet to find the maximum and minimum values of the solutions.

In addition to this, the worksheet can be used to analyze the behavior of the solutions over time. For example, the user can use the worksheet to determine how the solutions will change if the coefficients of the inequalities are changed.

Overall, the worksheet provides an invaluable tool for analyzing the solutions of systems of inequalities. It is an effective and efficient way of finding the solutions of these systems and analyzing their behavior.

Exploring the Role of Systems of Inequalities in Everyday Life

Systems of inequalities play a critical role in everyday life, impacting virtually all aspects of society. These inequalities are often rooted in economic and social factors, such as income and education, that can vary greatly between different individuals and groups.

In terms of economics, systems of inequality can be seen in the wage gap between genders and certain racial and ethnic groups. Women, for example, are typically paid less than men for equal work, and individuals from certain racial and ethnic backgrounds may be offered lower pay than their white counterparts. This creates an economic disparity between different groups, with those in the minority facing a greater challenge in maintaining a steady income and affording basic necessities.

In terms of social dynamics, systems of inequality can be seen in the way certain groups are treated differently or excluded from certain opportunities. For instance, people of color may be barred from certain educational institutions, or they may find that they are discriminated against when seeking employment or housing. This type of discrimination can have a lasting effect on individuals and their families, as it can limit their access to resources and opportunities that could help them to achieve financial stability.

Systems of inequality can also be found in areas such as healthcare and public services, where individuals from certain backgrounds may be denied access to the same level of care or services as those from more privileged backgrounds. This can have a profound effect on the health and wellbeing of individuals and communities as a whole, as those most in need may not have access to the same quality of care and services.

Overall, systems of inequality have a pervasive presence in everyday life, impacting individuals and communities in a variety of ways. While the issue of inequality is complex, it is clear that it has a significant impact on the lives of those it affects, and that efforts must be made to address it in order to create a more equitable society.

Using a Systems of Inequalities Worksheet to Solve Complex Problems

A systems of inequalities worksheet is a powerful tool for solving complex problems. It is a beneficial resource for students, teachers, and anyone else who needs to solve a problem with multiple variables.

The worksheet consists of a series of equations that represent the parameters of the problem. Each equation is written in the form of a linear inequality. By combining the equations and solving for the variables, one can find the solution to the problem.

When using a systems of inequalities worksheet, it is important to understand the different types of equations and how they can be used to solve the problem. Linear equations are equations that contain only one variable. Inequalities are equations that contain two or more variables. The equations can also be written in either standard or non-standard form.

Once the equations have been written, the next step is to solve the equations. This is done by combining the equations and solving for the variables. Through this process, the solution to the problem is found.

In order to use a systems of inequalities worksheet effectively, it is important to understand the meaning of the symbols used in the equations. For example, the symbol “<” indicates that the expression is less than or equal to the right side of the equation. The symbol “>” indicates that the expression is greater than or equal to the right side of the equation.

A systems of inequalities worksheet is a great resource for solving complex problems. It is an easy-to-use tool that can help students and teachers alike find the solution to a problem. By understanding the different types of equations and symbols used in the equations, one can successfully solve a problem with multiple variables.

Conclusion

The Systems of Inequalities Worksheet is a great tool for students to use in order to gain an understanding of how to solve systems of inequalities. By working through the worksheet, students can develop an understanding of how to graph inequalities, how to solve systems of inequalities using substitution or elimination, and how to interpret the solutions of systems of inequalities. This worksheet is an important tool for students to use in their math coursework and is an essential part of any math curriculum.