Exploring the Geometric Properties of Special Right Triangles: A Practice Worksheet

This worksheet is designed to help students explore the geometric properties of special right triangles. A special right triangle is a triangle with sides in the ratio of whole numbers such as 3:4:5, 5:12:13, or 7:24:25. Through the completion of this worksheet, students will learn the properties of special right triangles, including the relationship between the angles and sides, and the Pythagorean theorem.

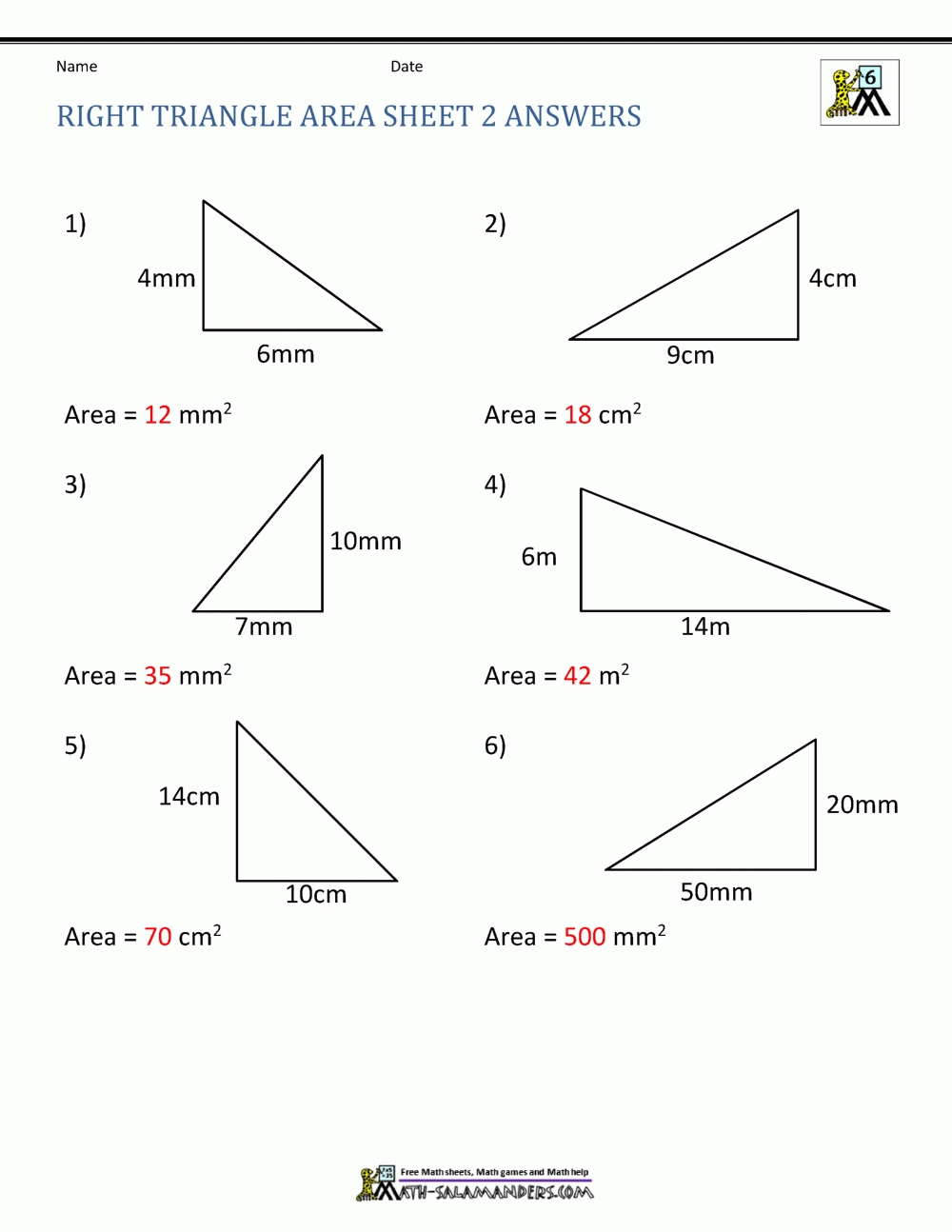
To begin, students must identify the sides of the special right triangle given. Using the ratios provided, students will calculate the length of each side and label the triangle accordingly. After labeling the triangle, students will calculate the missing angle. Using a protractor, students will measure the sides and angles of the triangle to verify that they are correct.

Next, students will use the Pythagorean theorem to calculate the length of the remaining side of the triangle. Using the lengths of the three sides, students can calculate the perimeter and area of the triangle. Lastly, students will use the properties of special right triangles to solve for missing lengths, angles, and areas of other special right triangles.

[toc]

By completing this worksheet, students will have a better understanding of the properties of special right triangles. They will learn how to calculate the sides and angles of these triangles, as well as how to use the Pythagorean theorem to find the missing side. Students will also gain a greater appreciation of the geometric properties of special right triangles, which can be applied to other areas of mathematics.

Analyzing the Pythagorean Theorem with Special Right Triangles: A Practice Worksheet

This practice worksheet is intended to help students analyze the Pythagorean Theorem with special right triangles. The worksheet begins by providing a brief overview of the Pythagorean Theorem and then progresses to examining specific right triangles and the application of the theorem to them.

The worksheet begins by introducing the Pythagorean Theorem. The theorem states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. This statement is expressed in the equation a2 + b2 = c2, where a and b are the shorter sides and c is the hypotenuse.

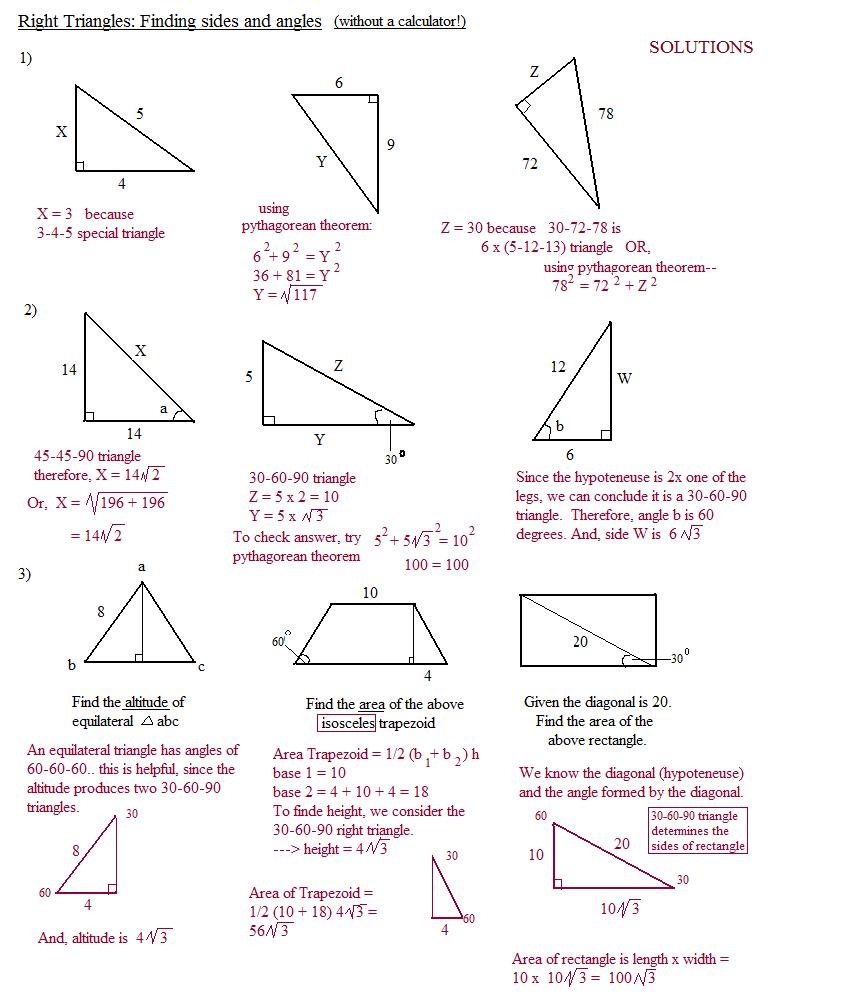
The worksheet then moves on to examining specific types of right triangles. These include 30-60-90 triangles, 45-45-90 triangles, and 3-4-5 triangles. For each type of triangle, the worksheet provides the lengths of the sides and then asks the student to calculate the hypotenuse of the triangle.

The worksheet also provides a few examples of how the Pythagorean Theorem can be used in real-world situations. One example is calculating the length of a ladder if you know the height and the angle of elevation. Another example is calculating the distance between two points on a map given the coordinates of the points.

By completing this practice worksheet, students will gain a better understanding of the Pythagorean Theorem and its application to special right triangles. This will help them to more effectively solve problems that involve right triangles.

Learning the Trigonometric Ratios of Special Right Triangles: A Practice Worksheet

Trigonometry is a branch of mathematics that studies the relationships between angles and sides of triangles. Knowing the trigonometric ratios of special right triangles can be very helpful in solving problems in a variety of fields. This practice worksheet is designed to help you learn the trigonometric ratios of special right triangles.

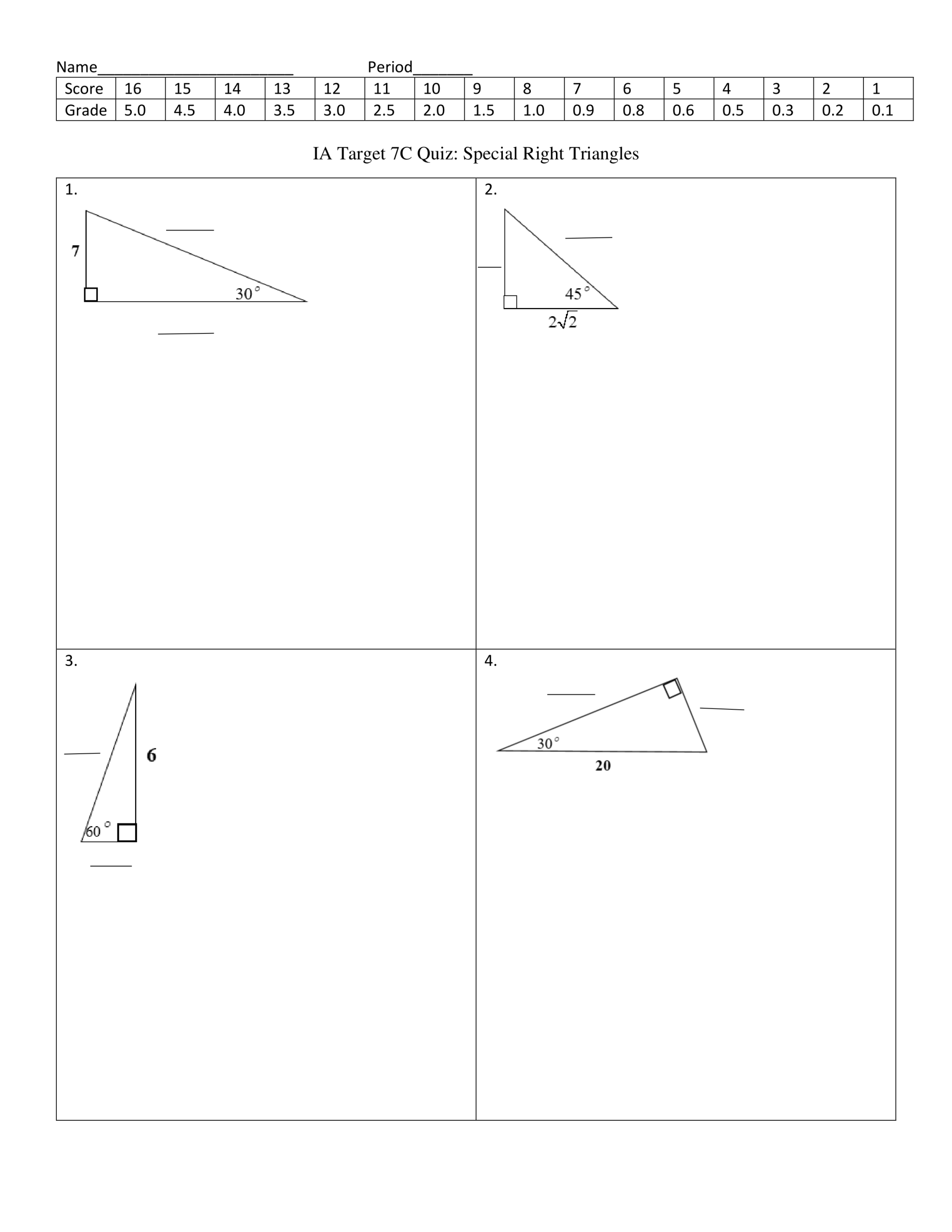
This worksheet is composed of four parts. In the first part, you will be provided with the side lengths of several special right triangles and asked to calculate the corresponding trigonometric ratios. The second part of the worksheet will require you to identify special right triangles given the trigonometric ratios. The third part will involve solving equations using the trigonometric ratios of special right triangles. Finally, in the last part, you will be asked to solve problems involving angle of elevation or angle of depression.

To complete this worksheet, you will need to have a basic understanding of the following concepts: trigonometric ratios, the Pythagorean theorem, and the definitions of acute, right, and obtuse angles. Additionally, you may find it helpful to have a calculator and a ruler available.

By following the instructions and completing each part of the worksheet, you will gain a deeper understanding of the trigonometric ratios of special right triangles and learn how to apply them to solve equations and problems.

Conclusion

This Special Right Triangles Practice Worksheet has been an excellent tool in helping us understand the properties of special right triangles. We have been able to recognize the different ratios and use them to solve for missing sides and angles. We have also been able to apply our knowledge to real-world problems, such as finding the area and perimeter of a right triangle. With a better understanding of special right triangles, we can now apply our knowledge to a variety of other mathematical problems.

[addtoany]