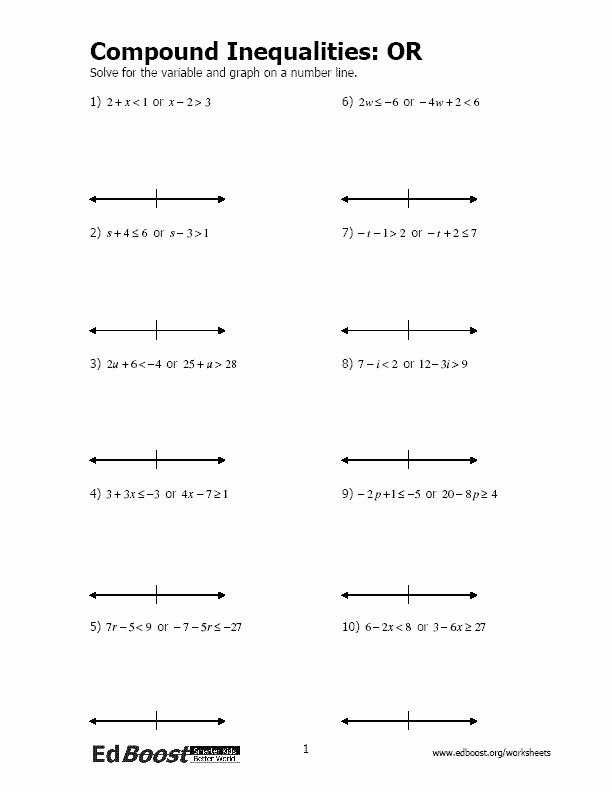
How to Use a Solving Compound Inequalities Worksheet to Improve Math Skills

Using a solving compound inequalities worksheet is an effective way to improve math skills. A compound inequality is a mathematical expression that includes two inequalities that are joined by either “and” or “or.” Solving compound inequalities requires knowledge of algebraic operations, such as combining like terms and solving linear equations.

When using a worksheet to improve math skills, it is important to make sure that the worksheet is comprehensive and allows for practice. The worksheet should include examples of compound inequalities, as well as instructions for solving them. Additionally, the worksheet should provide ample space for students to practice solving the compound inequalities. This will enable them to become more comfortable with the algebraic operations required to solve these equations.

When completing a worksheet, students should be encouraged to read and understand the instructions given. This will enable them to properly identify the inequalities, as well as understand how to solve them. Additionally, students should be encouraged to make note of any errors made during the solving process, as this will help them identify where they may need additional practice.

[toc]

Once the worksheet is complete, students should be encouraged to review their work and check for accuracy. It is also important to have students explain why they solved the compound inequality in the way they did. This will help them further their understanding of the material.

By using a solving compound inequalities worksheet, students can gain a better understanding of these equations and become more proficient in math. Through practice, they can become more comfortable with the algebraic operations needed to solve these equations and thus improve their math skills.

A Step-by-Step Guide to Solving Compound Inequalities

Solving a compound inequality involves breaking down the inequality into two separate inequalities and then solving them separately. This step-by-step guide will walk you through the process of solving a compound inequality.

Step 1: Determine the inequality sign.

The first step in solving a compound inequality is to determine the inequality sign. Compound inequalities have two inequality signs, one that is placed between the two expressions, and one that is placed at the end of the inequality. The type of inequality sign used will determine which of the two expressions should be solved first.

Step 2: Rearrange the inequality.

The second step is to rearrange the inequality so that the variables are on one side and the constants are on the other. This is done by subtracting or adding both sides of the inequality to get the variables on one side and the constants on the other.

Step 3: Solve for the variable.

Once you have rearranged the inequality, you can solve for the variable by using the appropriate algebraic operation. Depending on the type of inequality, you may need to use addition, subtraction, multiplication, or division. Once you have solved for the variable, you will have two separate inequalities.

Step 4: Solve the two inequalities.

The fourth step is to solve the two inequalities. This can be done by first graphically plotting the two inequalities on a number line. Then, you can identify the regions of the number line that satisfy both inequalities. These regions are known as the solution set.

Step 5: Check your answer.

The fifth and final step is to check your answer. To do this, you should plug a few values into the original compound inequality and make sure that they satisfy the inequality. This will help you make sure that you have correctly solved the compound inequality.

By following these five steps, you can easily solve a compound inequality. Remember to always double-check your answer to make sure that it is correct.

Creative Strategies for Solving Compound Inequalities

Compound inequalities are equations that involve two or more inequalities joined together with the words ‘and’ or ‘or’. Solving these types of equations can often be a challenge. Fortunately, there are several creative strategies that can be used to solve compound inequalities.

One of the most effective strategies is to first combine the two inequalities into one equation. This can be done by multiplying or dividing both sides of the equation by the same number, or by adding or subtracting the same number from both sides of the equation. This will result in a single equation that can then be solved using standard methods.

Another strategy is to use a graph to solve the compound inequality. This involves plotting the two inequalities on the same graph, then manipulating the graph until the solution is found. This can be done by shifting the graph, stretching it, or compressing it, depending on the equation.

Finally, another strategy is to use a combination of both methods. First, combine the equations into one equation, then solve it graphically. This can be done by plotting the solution on the graph, then manipulating the graph until the solution is found. This approach can be especially useful for complex equations that cannot be solved using standard methods.

These creative strategies can be used to solve compound inequalities quickly and accurately. With the right approach, these equations can become much easier to solve.

Understanding Compound Inequalities and How to Solve Them

A compound inequality is a statement that combines two inequalities that share the same variable. The two inequalities that make up a compound inequality can be either two different types of inequalities (e.g., greater than and less than) or the same type of inequality (e.g., greater than or equal to and greater than or equal to). In order to solve a compound inequality, one must first identify the two inequalities and then combine them into one by using the logical connective “and” or “or”.

Once the compound inequality is formed, the solution can be found by graphing the two inequalities on the same coordinate plane and then finding the intersection of the two lines. The solution of the compound inequality is the set of all points that lie in the intersection of the two lines. For example, if the two inequalities are y > 2 and y < 4, then the intersection of the two lines will be the set of all points (x, y) such that 2 < y < 4. Alternatively, one can solve a compound inequality algebraically. In order to do so, one must first isolate the variable on one side of the inequality. Then, if the compound inequality is of the form "x < a and x > b” or “x > a and x < b", one can simply solve for the variable by taking the average of the two numbers (a + b)/2. If the compound inequality is of the form "x ≥ a and x ≤ b" or "x ≤ a and x ≥ b", one can solve for x by taking the maximum of the two numbers (max(a, b)). By understanding how to solve compound inequalities, one can more easily identify and solve problems involving two or more inequalities.

Conclusion

In conclusion, the Solving Compound Inequalities Worksheet is a great way to practice and strengthen your skills in solving compound inequalities. It is important to understand the different types of compound inequalities and how to solve them, as they are often used in real-life situations. With practice, you can become proficient in solving compound inequalities and use them to your advantage.

[addtoany]