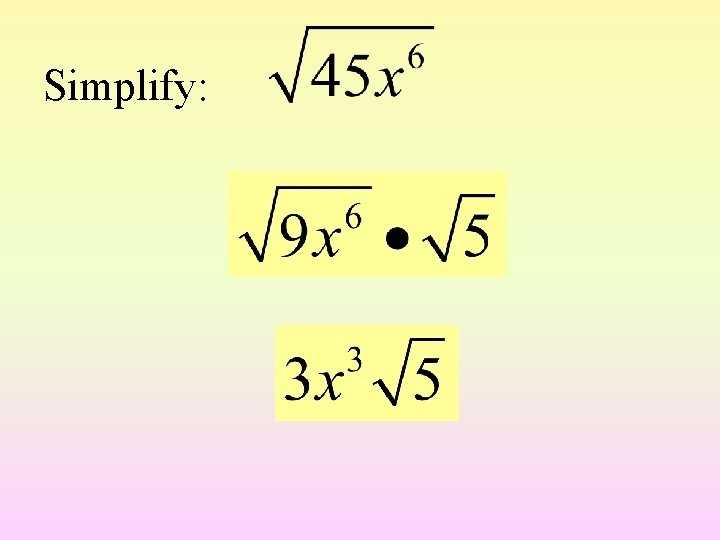How to Use a Simplifying Radicals Worksheet to Strengthen Your Algebra 2 Skills

Using a simplifying radicals worksheet is an excellent way to strengthen your algebra 2 skills. A simplifying radicals worksheet is a great tool to use when teaching, or learning, the properties of radicals and how to simplify them. By following the steps provided, students can gain a better understanding of how to simplify and manipulate radicals.

First, students should begin by reviewing the basic rules for simplifying radicals. This includes understanding the definition of a radical, the rules of exponentiation, the power rule, the product rule, and the quotient rule. Once these basic rules are reviewed, students should be able to identify any radicals within a given problem.

Next, students should use the rules of exponentiation to simplify the radicals. This means that any number that is raised to a power should be multiplied by itself the number of times indicated by the power. Once the radicals are simplified, the student should then move onto the power rule. This rule states that any number raised to a negative power should be turned into a reciprocal.

The product and quotient rules should then be applied to the radicals. The product rule states that when radicals are multiplied, the product is equal to the product of the radicals multiplied together. The quotient rule states that when radicals are divided, the quotient is equal to the quotient of the radicals divided together.

Finally, students should apply the simplifying radicals worksheet to practice manipulating and simplifying radicals. By completing the worksheet, students will be able to identify patterns and gain a better understanding of the rules for simplifying radicals. As students become more comfortable with the worksheet, they can then use it to help solve more complex problems.

By utilizing a simplifying radicals worksheet, students can strengthen their algebra 2 skills and become more confident in their ability to solve problems involving radicals. This worksheet is a great way for students to practice their knowledge of radicals and gain a deeper understanding of the rules for simplifying them.

Unraveling the Mysteries Behind Simplifying Radicals: An Overview for Algebra 2 Learners

Algebra 2 learners often encounter the concept of simplifying radicals during their course of study. This process can seem quite daunting and mysterious for those who are not well-versed in the subject area. However, by breaking down the process into small, manageable steps, learners can gain a better understanding of the process and increase their confidence.

In order to simplify a radical, it is important to understand the basic components of a radical expression. A radical expression is a mathematical expression that contains a square root or cube root symbol. The radicand is the number or expression that is contained beneath the radical symbol. This is the expression that is simplified in the process of simplifying the radical.

The first step of simplifying a radical expression is to factor the radicand. This involves breaking it down into its prime factors. The prime factors of a number are the prime numbers that can be multiplied together to produce the number. Once the radicand is factored, it is then necessary to look for perfect squares, which are numbers that can be expressed as the product of two identical factors. It is possible to simplify the radical by taking out any perfect squares that exist.

The next step in simplifying a radical is to add any remaining factors of the radicand that are not perfect squares. These are left inside the radical symbol and can be combined with like terms if they exist. Finally, the radical can be simplified further by taking out any common factors of the radicand that remain inside the radical symbol. This is done by dividing the radicand by the common factor.

By following the steps outlined above, algebra 2 learners can successfully simplify radical expressions. With practice, learners will gain a better understanding of the process and be able to confidently work through problems involving radicals. As with any mathematical concept, it is important to remember that practice is the key to mastering the skill.

Practical Tips for Mastering Simplifying Radicals with Algebra 2 Worksheets

1. Understand the concept: Simplifying radicals is an important concept in algebra 2, and it is important to have a good understanding of the underlying principles. Take the time to review the concept and make sure you understand what a radical expression is and how to simplify it.

2. Use practice problems: Once you understand the concept, practice it by working through practice problems. Algebra 2 worksheets provide a great way to get started. Look for worksheets that provide step-by-step guidance for simplifying radicals and work through them systematically.

3. Review the rules: Simplifying radicals requires you to apply a set of rules. Make sure you are familiar with these rules and can apply them correctly.

4. Check your answers: When you’re done, make sure to check your answers. You can use a calculator to check your work, or you can use a worksheet answer key. Either way, it’s important to check your work to make sure you’ve simplified the radical correctly.

5. Take your time: Don’t rush when simplifying radicals. Take your time and think through each step carefully. This will help to ensure you get the correct answer and understand the concept better.

Conclusion

The Simplifying Radicals Worksheet Algebra 2 provides an excellent opportunity for students to practice their skills in manipulating and rationalizing radical expressions. By working through the worksheet, students can gain a better understanding of the concepts and become more confident in their ability to solve radical equations. This worksheet can help students develop a strong foundation in algebraic manipulation and rationalizing, which can then be applied to more complex topics.