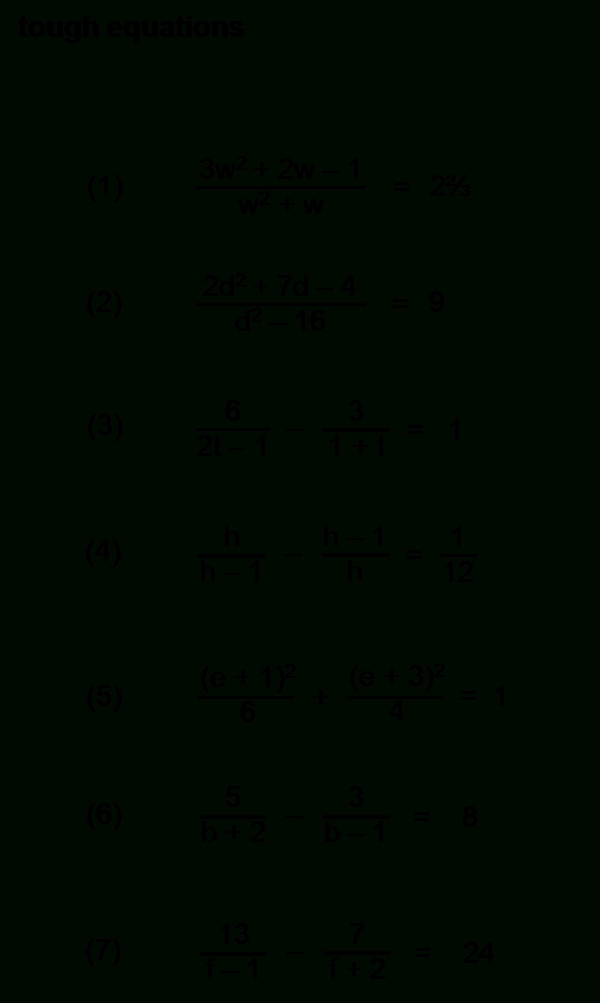How to Make Algebraic Fractions Simple with Worksheets

Algebraic fractions can be intimidating for students. However, with the right worksheets and a few simple steps, students can make these fractions easy to understand.

The first step is to identify each fraction as either a proper fraction or an improper fraction. A proper fraction is a fraction that has a numerator that is less than its denominator. An improper fraction is a fraction whose numerator is larger than its denominator.

Once the student has identified the fractions, they can begin to simplify them. To do this, the student will need to find the greatest common factor of the numerator and denominator of the fraction. This can be done by dividing each number by the same number until a remainder of zero is reached. The number that was divided is the greatest common factor.

Once the greatest common factor is found, the student can divide the numerator and denominator of the fraction by the greatest common factor. This will simplify the fraction to its lowest terms.

Worksheets can be a great resource when attempting to simplify algebraic fractions. Many worksheets are available online, and they provide step-by-step instructions on how to simplify fractions.

By using worksheets and following these steps, students will be able to make algebraic fractions simple. With a bit of practice, they should soon be able to quickly and accurately simplify fractions.

Understanding the Basics of Simplifying Algebraic Fractions with Worksheets

Algebraic fractions can be difficult to understand, but with the help of worksheets, students can get a better grasp of the basics of simplifying algebraic fractions.

Worksheets are a great tool for learning, as they provide a range of questions that can help students understand the basics of algebraic fractions. By working through these worksheets, students can practice their problem-solving skills and learn how to simplify fractions.

When simplifying algebraic fractions, there are several steps to follow. First, students need to identify the numerator and denominator of the fraction. Then, they must factor out any common factors that appear in both the numerator and denominator. This will result in a simplified fraction.

Next, students need to recognise any terms that can be cancelled out. This is when a factor appears in both the numerator and denominator and can be removed. For example, if the numerator contains 3x and the denominator contains 6x, then the 3x and the 6x can both be cancelled out, leaving the fraction equal to x.

Finally, students must reduce the fraction to its lowest terms. This can be done by dividing both the numerator and denominator by the same number until no more division is possible. For example, if the numerator of a fraction is 12 and the denominator is 18, then the fraction can be reduced to 2/3.

By working through worksheets that require students to simplify algebraic fractions, students can gain a greater understanding of the process. By using these worksheets, students can practice their problem-solving skills and become more proficient in simplifying algebraic fractions.

Step-by-Step Guide to Simplifying Algebraic Fractions with Worksheets

Algebraic fractions can be daunting to simplify, but with the right steps, anyone can do it! Follow this step-by-step guide to simplify fractional expressions with confidence.

Step 1: Identify the Numerator and Denominator

The first step to simplifying any fraction is to identify the numerator (the top number) and the denominator (the bottom number). It is important to remember that the numerator represents the number of parts and the denominator represents the total number of parts in the whole.

Step 2: Find the Greatest Common Factor (GCF)

The next step is to find the Greatest Common Factor, or GCF. This is the largest number that divides both the numerator and the denominator evenly. To determine the GCF, list all the factors of the numerator and the denominator, then look for the greatest factor common to both.

Step 3: Divide the Numerator and Denominator by the GCF

Once the GCF has been determined, it must be divided into both the numerator and denominator. This will result in a simplified fraction, but it may not be in its simplest form.

Step 4: Simplify the Fraction

The last step is to simplify the fraction by finding any common factors between the numerator and the denominator. If there is a common factor, divide both the numerator and denominator by the factor to get the simplest form of the fraction.

Using Worksheets

To practice simplifying fractions, worksheets can be a great help. By completing worksheets, students can practice the steps outlined above and get a better understanding of how simplifying fractions works. Worksheets can also help students develop their skills and confidence in simplifying algebraic fractions.

By following the four simple steps above, anyone can learn to simplify algebraic fractions with confidence. With practice, and the help of worksheets, it can become second nature.

Conclusion

The simplifying algebraic fractions worksheet is a great tool for students to use when learning how to simplify fractions. It provides students with sample problems and solutions, which can help them learn the basics of simplifying fractions. With practice, students can develop a better understanding of how to solve algebraic fractions and apply their knowledge to real-world problems.