Exploring the Mathematics Behind Proving Lines Parallel Worksheet Answers

Exploring the mathematics behind proving lines parallel is an educational exercise that provides a valuable opportunity to understand the fundamental principles of geometry. In this worksheet, students will learn how to use a variety of tools, such as transversals, angles, and slopes, to prove that two lines are parallel.

To begin, students must understand the concept of parallel lines. Parallel lines are two or more lines in a plane that never intersect. This means that the lines are always going in the same direction and never cross. In order to prove that two lines are parallel, students need to identify certain characteristics that indicate the lines are parallel.

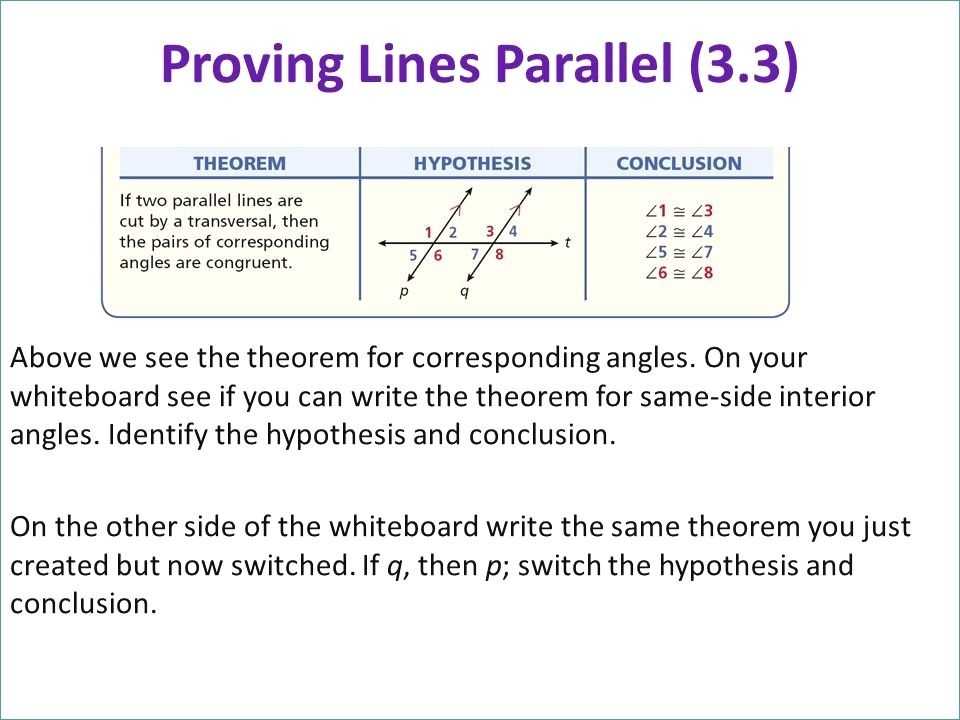
One of the most commonly used methods of proving lines parallel is the Angle-Angle Postulate. This postulate states that if two angles are congruent (have the same measure), then the lines that form them are parallel. To use this postulate, students need to find two angles that have the same measure. Then, they can conclude that the lines that form those angles are parallel.

[toc]

Another method of proving lines parallel is the Slope-Intercept Postulate. This postulate states that if two lines have the same slope, then they are parallel. To use this postulate, students must use the equation for a line to find the slope of each line. If the two slopes are the same, then the lines are parallel.

Finally, students can use transversals to prove that two lines are parallel. A transversal is a line that intersects two other lines. When two lines are parallel, the angles formed by the transversal and the two lines are all equal. By measuring these angles and ensuring that they are all equal, students can prove that the two lines are parallel.

By completing this worksheet, students will have a better understanding of the mathematics behind proving lines parallel. They will be able to use the Angle-Angle Postulate, the Slope-Intercept Postulate, and transversals to prove that two lines are parallel. This is a valuable skill that will help in many aspects of geometry.

How to Use Proving Lines Parallel Worksheet Answers to Master Geometry Concepts

Proving Lines Parallel worksheet answers are an invaluable tool for mastering the concepts of geometry. Using the worksheet answers can help students understand the various elements of geometry and how to apply them to real world problems.

To best use the Proving Lines Parallel worksheet answers, students should first read the questions carefully and make sure they understand what is being asked. Then, they should read through the worksheet answers and determine which of the answers is correct and which ones are incorrect. Finally, students should take the time to practice solving the problems on the worksheet and learn how to apply the concepts to their own work.

When studying geometry, it is important to have a strong understanding of the basic principles. This includes understanding the definitions of parallel lines, perpendicular lines, and lines of symmetry. Knowing the definitions of these terms will help students understand the different properties of these shapes and how they can be used to solve problems.

The Proving Lines Parallel worksheet answers also provide students with examples of problems that use the principles of geometry. This can be used to help students understand how to apply the concepts to their own work. By studying the examples, students can become more familiar with the concepts and be better prepared to solve problems on their own.

Finally, students should practice solving the problems on the worksheet using the Proving Lines Parallel worksheet answers. This will help them gain a better understanding of the concepts and be better prepared to solve problems on their own. Through practice, students can master the concepts of geometry and understand how to use them to solve real world problems.

Common Mistakes to Avoid When Proving Lines Parallel with Worksheet Answers

1. Misinterpreting the Prompt: When attempting to prove that two lines are parallel using a worksheet, it is important to read the prompt carefully. If the prompt is asking for an example of how two lines are parallel through the use of a worksheet, the answer should focus on how the worksheet can be used to prove the lines are parallel.

2. Not Label Points and Lines Clearly: When attempting to prove that lines are parallel using a worksheet, it is important to label each point and line clearly. This will help avoid confusion and ensure that the lines are being compared accurately.

3. Not Understanding the Meaning of Parallel: When attempting to prove that two lines are parallel, it is important to have a clear understanding of the meaning of parallel. In this case, parallel means that two lines are the same distance apart from each other, no matter how long or short the lines are.

4. Not Drawing Accurate Diagrams: When attempting to prove that two lines are parallel using a worksheet, it is important to draw accurate diagrams. This will ensure that the lines are being compared accurately, and it will also help to illustrate the proof.

5. Not Focusing on the Details: When attempting to prove that two lines are parallel using a worksheet, it is important to focus on the details. This includes making sure that the angles are equal, and that the lines are the same distance apart.

6. Not Using the Worksheet: When attempting to prove that two lines are parallel, it is important to use the worksheet to its full potential. This means that all relevant information should be included in the proof, such as points, angles, and distances.

Different Approaches to Solving Proving Lines Parallel Worksheet Answers

1. Visualizing: Visualizing the lines being parallel is one of the most effective ways of determining if two lines are parallel. It is important to draw the lines accurately and use a ruler to make sure that the lines are equal in length and the angles are the same. Additionally, it is important to draw the lines with a consistent scale. This allows students to compare the angles and lengths of the lines and determine if they are parallel.

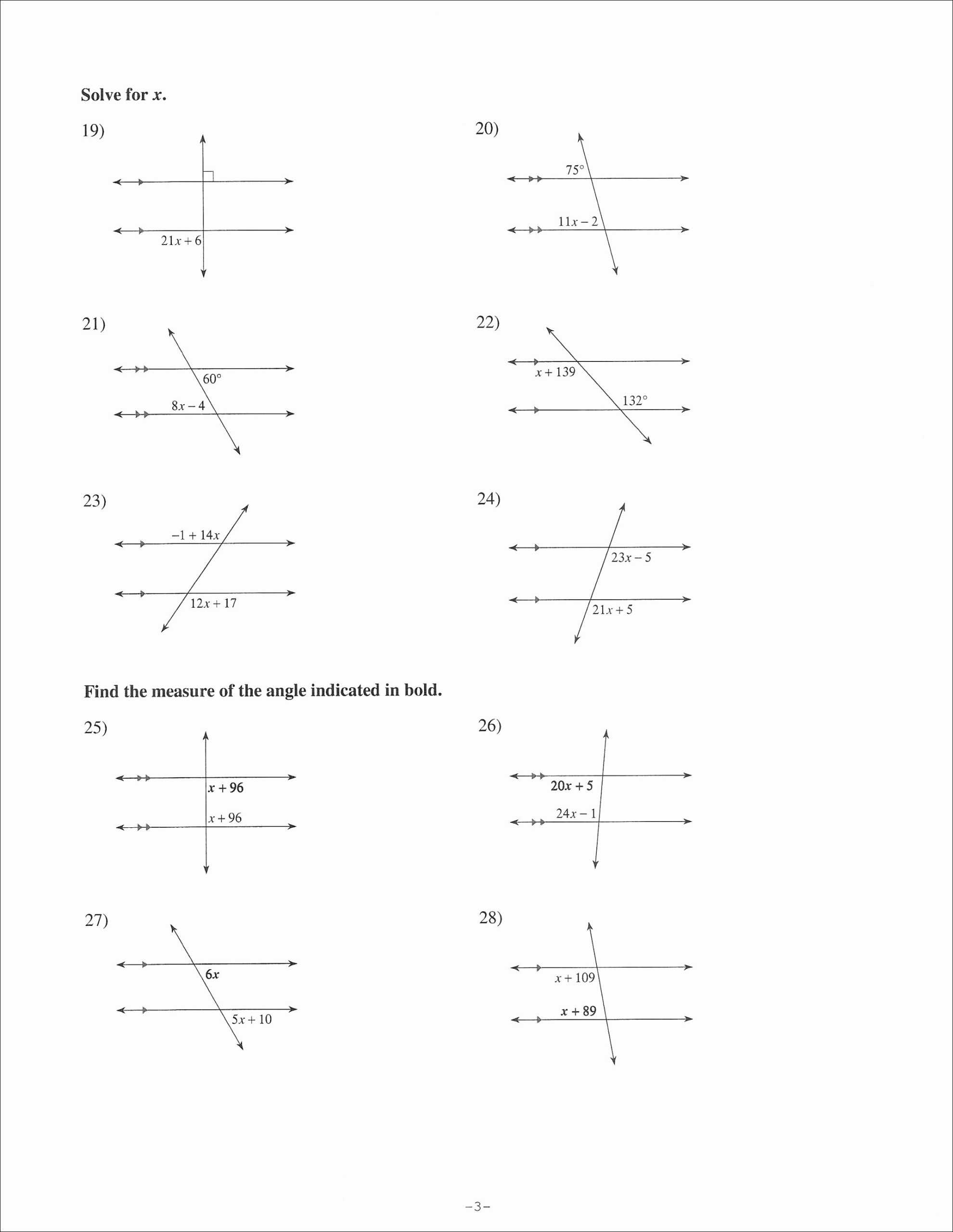
2. Angle Measurement: Another approach to proving lines parallel is to use the angle measurement method. This involves measuring the angles of the lines and determining if they are equal. This method can be used to prove parallelism by measuring the same angle on both lines and verifying that they are equal.

3. Using Slopes: Proving lines parallel can also be done by using the slope method. This involves calculating the slopes of both lines and comparing them. If the slopes are equal, then the lines are parallel. Additionally, if the slopes are not equal, then the lines are not parallel.

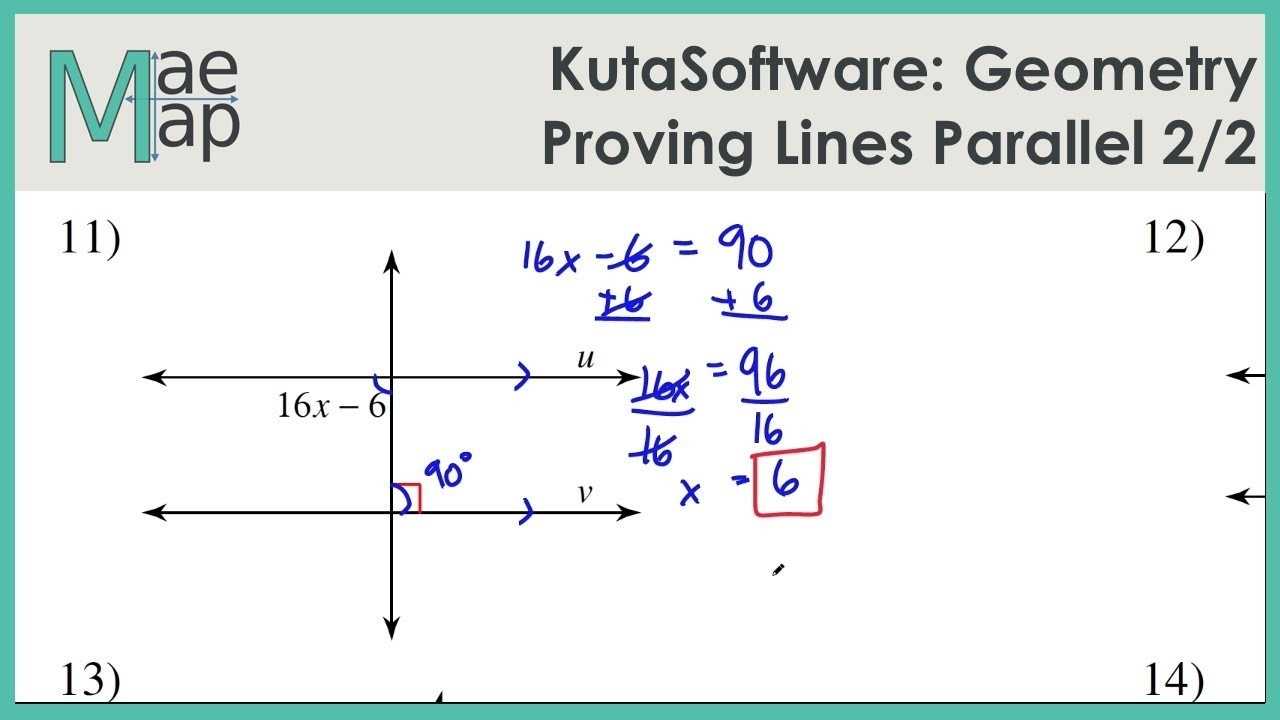
4. Using Transversal: When using the transversal method, students measure the angles formed by a transversal line intersecting two lines. If all angles are equal, then the two lines are parallel. This worksheet can be used to introduce students to transversal lines, angles, and the concept of parallelism.

5. Using Perpendicular Bisector: Proving lines parallel can also be done by using the perpendicular bisector method. This involves drawing a line perpendicular to both lines and then measuring the angles created. If the angles are equal, then the lines are parallel. This worksheet can be used to introduce students to perpendicular bisectors, angles, and the concept of parallelism.

Conclusion

The Proving Lines Parallel Worksheet Answers demonstrate the importance of understanding the properties of parallel lines. They help reinforce the fact that when two lines are parallel, they never cross and have the same slope. They are also an important tool used to prove that two lines are parallel. By using the provided worksheet, students can learn how to correctly apply the properties of parallel lines in order to determine if two lines are parallel.

[addtoany]