Exploring the Properties of Real Numbers: A Step-by-Step Guide to the Worksheet

Welcome to the Real Numbers Worksheet! This worksheet aims to help you understand the properties of real numbers, which are the basis of mathematics. We will start by discussing the definition of real numbers and then explore their properties.

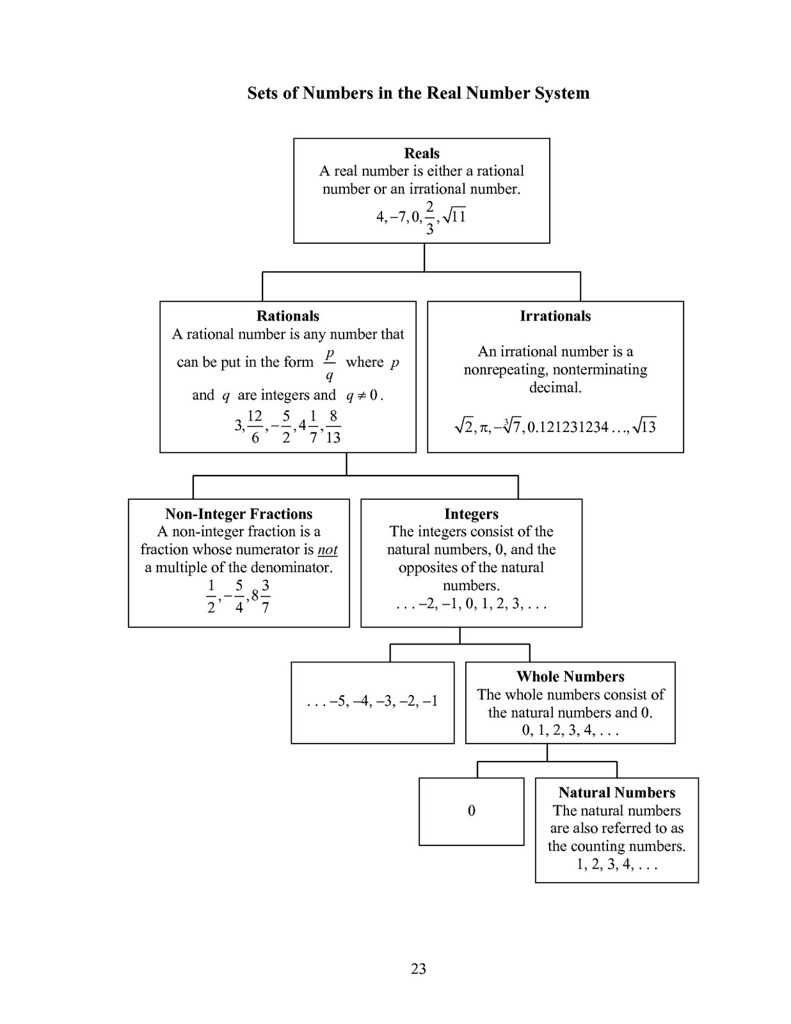
Real numbers are numbers that can be represented on a number line. This includes all integers and fractions, as well as irrational numbers, such as the square root of two. All real numbers can be classified as either rational or irrational. Rational numbers are those that can be expressed as the ratio of two integers, and are the most common type of real number. Irrational numbers, on the other hand, cannot be expressed as the ratio of two integers.

Now that you know what real numbers are, let’s explore their properties.

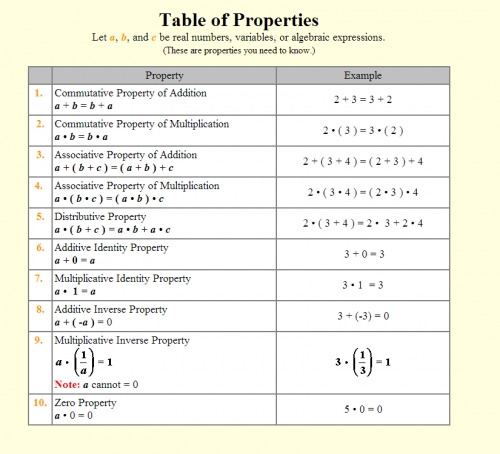
The first property of real numbers is the distributive property. This property states that when two real numbers are multiplied, the product is equal to the sum of the multiplicands multiplied separately. For example, if you were to multiply the real numbers 4 and 5, the product would be 20, which is equal to 4 times 5 plus 5 times 4.

The second property of real numbers is the commutative property. This property states that when two real numbers are multiplied, the order of the multiplicands does not affect the product. This means that 4 times 5 is the same as 5 times 4, and the product will always be 20.

The third property of real numbers is the associative property. This property states that when three or more real numbers are multiplied, the order of the multiplicands does not affect the product. This means that 4 times 5 times 6 is the same as 4 times 6 times 5, and the product will always be 120.

The fourth property of real numbers is the closure property. This property states that the result of any operation performed on two real numbers will always be a real number. This means that if you add two real numbers together, the result will always be a real number. It also means that if you subtract two real numbers, the result will always be a real number.

Finally, the fifth property of real numbers is the identity property. This property states that any real number multiplied by one will remain unchanged. This means that if you multiply 4 by 1, the result will still be 4.

We hope that this worksheet has helped you understand the properties of real numbers. Now that you know more about them, you will be able to use these properties to solve mathematical problems with ease.

How to Use the Properties of Real Numbers to Solve Complex Math Problems

Solving complex math problems often requires an understanding of the properties of real numbers. Real numbers are all the numbers on the number line, including the rational, irrational, integer, and complex numbers. Each type of real number has certain properties that can be used to solve complex math problems.

One of the most important properties of real numbers is the associative property. This property states that when two or more operations are combined, the order in which they are combined does not matter. For example, when adding or multiplying three or more numbers, the result is the same regardless of the order in which the numbers are grouped and added or multiplied. This property can be used to simplify complex equations and to help solve complex math problems.

Another important property of real numbers is the distributive property. This property states that when two terms are multiplied by the same factor, the product of the terms can be found by multiplying the factor by each of the terms separately. This property can be used to simplify complex equations, and to help solve complex math problems.

The commutative property is also an important property of real numbers. This property states that when two or more operations are performed on the same number, the order in which they are performed does not matter. This property can be used to simplify complex equations and to help solve complex math problems.

Finally, the transitive property is also an important property of real numbers. This property states that if two numbers are related by one operation, and that relationship is the same as the relationship between two other numbers, then the two numbers are related by the same operation. This property can be used to simplify complex equations and to help solve complex math problems.

By understanding and applying the properties of real numbers, complex math problems can be solved with ease. Using the associative, distributive, commutative, and transitive properties, complex equations can be simplified and complex math problems can be solved.

The Benefits of Learning the Properties of Real Numbers: What You Need to Know Before Doing the Worksheet

Learning the properties of real numbers is an important part of any mathematics curriculum. The properties of real numbers are essential for understanding a range of mathematical concepts, from basic arithmetic to more advanced concepts. Understanding these properties is also important for developing problem-solving skills and forming a strong foundation in mathematics.

Before attempting any worksheet on the properties of real numbers, it is important to understand the following concepts. Firstly, real numbers include all the numbers on the number line, including fractions, decimals, and integers. Secondly, the four main operations that can be performed on real numbers are addition, subtraction, multiplication, and division. These operations can be used to solve equations, understand relationships between numbers, and calculate solutions to problems.

In addition, it is important to understand the properties that govern the behavior of real numbers. These properties include the associative, distributive, commutative, and identity properties. Each of these properties is related to the way in which the operations of addition, subtraction, multiplication, and division interact with real numbers.

Furthermore, it is important to understand the concept of absolute value in order to solve problems involving real numbers. Absolute value is the distance a number is from zero and is represented by two vertical lines enclosing the number.

Finally, it is important to understand the concept of inequality and how to use it to solve problems involving real numbers. Inequality is the comparison of two or more numbers using the symbols “<”, “>”, “≤” and “≥”.

By understanding these concepts before attempting to solve a worksheet on the properties of real numbers, students will be well-prepared to tackle the worksheet and gain a deeper understanding of real numbers.

Conclusion

This properties of real numbers worksheet has provided a great introduction to the basics of real numbers. By exploring the different properties of real numbers, students have been able to gain a better understanding of the foundations of mathematics. In addition, this worksheet has provided students with a better appreciation of the importance of understanding the properties of real numbers and how they can help them in their mathematical studies.