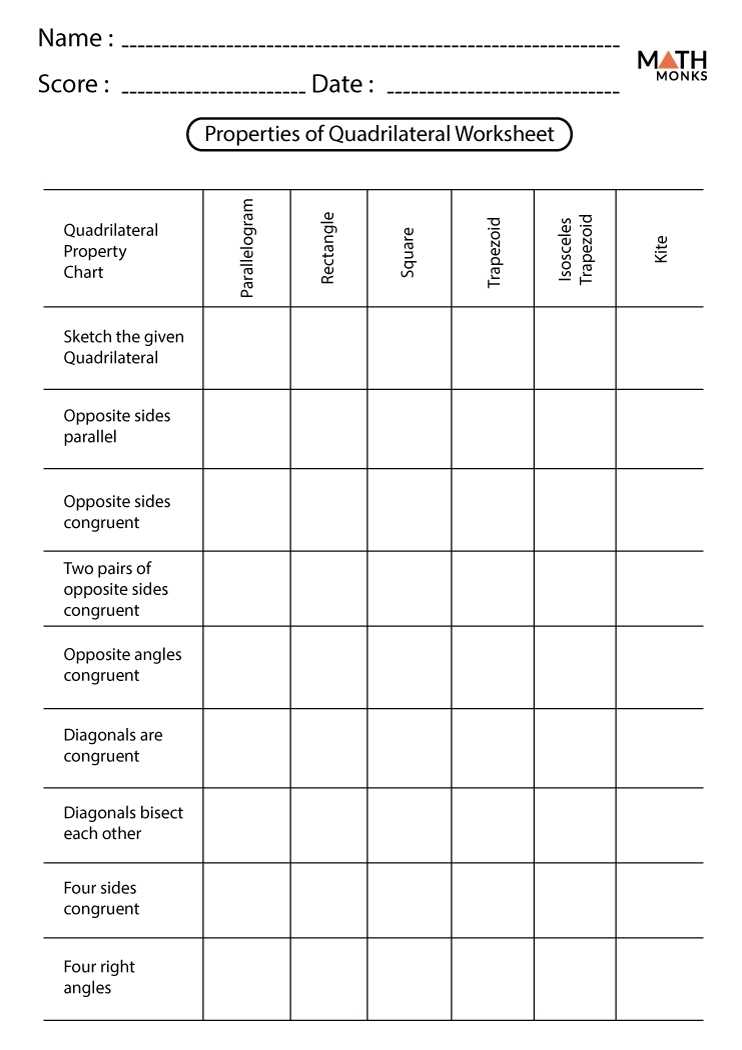
How to Use Properties of Quadrilaterals Worksheets to Teach Geometry

Teaching geometry to students can be a difficult task, but using properties of quadrilaterals worksheets can help to make the learning process more engaging and effective. Properties of quadrilaterals worksheets are a tool that teachers can use to help students learn the various properties that define different types of quadrilaterals. These worksheets provide students with practice in recognizing and applying the properties of quadrilaterals and can be used as part of a lesson plan or as a homework assignment.

To use properties of quadrilaterals worksheets effectively, teachers should begin by introducing the different types of quadrilaterals and their properties. Once students understand the basic definitions and characteristics of each type, they can then use the worksheets to practice applying the properties. Worksheets typically include questions that require students to identify the type of quadrilateral based on its properties, as well as questions that ask them to use the properties to calculate certain measurements.

After introducing the topic, teachers can provide students with a worksheet to complete on their own. After students have completed the worksheet, teachers can use it as an opportunity to review the properties of quadrilaterals and to discuss any questions or difficulties that students may have encountered. Through this review and discussion, teachers can ensure that students have a clear understanding of the concepts and are able to correctly apply the properties of quadrilaterals in various types of problems.

Using properties of quadrilaterals worksheets can be a great way to engage students in learning geometry. By introducing and discussing the properties, and providing students with practice problems, teachers can help ensure that students understand the underlying concepts behind geometry and are able to apply them in the future.

Exploring the Different Types of Quadrilaterals and Their Properties

Quadrilaterals are four-sided geometric shapes with properties that distinguish them from other shapes. A fundamental part of geometry, quadrilaterals come in many varieties, each with distinct characteristics that set it apart from the rest.

The most basic type of quadrilateral is the parallelogram. Four sides in a parallelogram are all equal in length, with two of its sides parallel and two pairs of opposite sides equal in size. The angles of a parallelogram add up to 360 degrees, making them a type of convex polygon. The most familiar example of a parallelogram is the rectangle, which is distinguished by having four right angles. Other kinds of parallelograms include rhombi, which have four equal sides, and trapezoids, which have one pair of parallel sides.

Another type of quadrilateral is the kite, which has two pairs of adjacent sides that are equal in length but not parallel. Kites are also convex polygons, but the angles in a kite do not add up to 360 degrees.

The third type of quadrilateral is the trapezoid, which has two parallel sides and two non-parallel sides. Trapezoids are also convex polygons, with angles that add up to 360 degrees.

The final type of quadrilateral is the quadrilateral, which is distinct in that its four sides are not parallel and its angles do not add up to 360 degrees. The most common type of quadrilateral is the square, which has four equal sides and four right angles.

Each type of quadrilateral has its own unique properties that set it apart from the others. Understanding the different characteristics of quadrilaterals is an important aspect of geometry, as it allows us to identify and classify different shapes.

Analyzing Quadrilateral Properties Through Visual Representation

Quadrilateral properties can be easily analyzed through visual representation. A quadrilateral is a plane figure with four sides and four angles. Visual representation of this figure is useful in understanding the various properties associated with it.

By using diagrams and other visual tools, the properties of a quadrilateral can be quickly discerned. For example, one can determine the type of quadrilateral based on the lengths of its sides and the measures of its angles. A quadrilateral with four equal sides and four equal angles is a square. A quadrilateral with two pairs of parallel sides and four equal angles is a parallelogram. Other types of quadrilaterals include trapezoids, rectangles, and rhombuses.

Visual representation can also help to understand the relationships between the angles, sides, and diagonals of a quadrilateral. For example, the interior angles of a quadrilateral always add up to 360 degrees. The diagonals of a parallelogram bisect each other, while the diagonals of a rectangle are perpendicular and bisect each other at right angles.

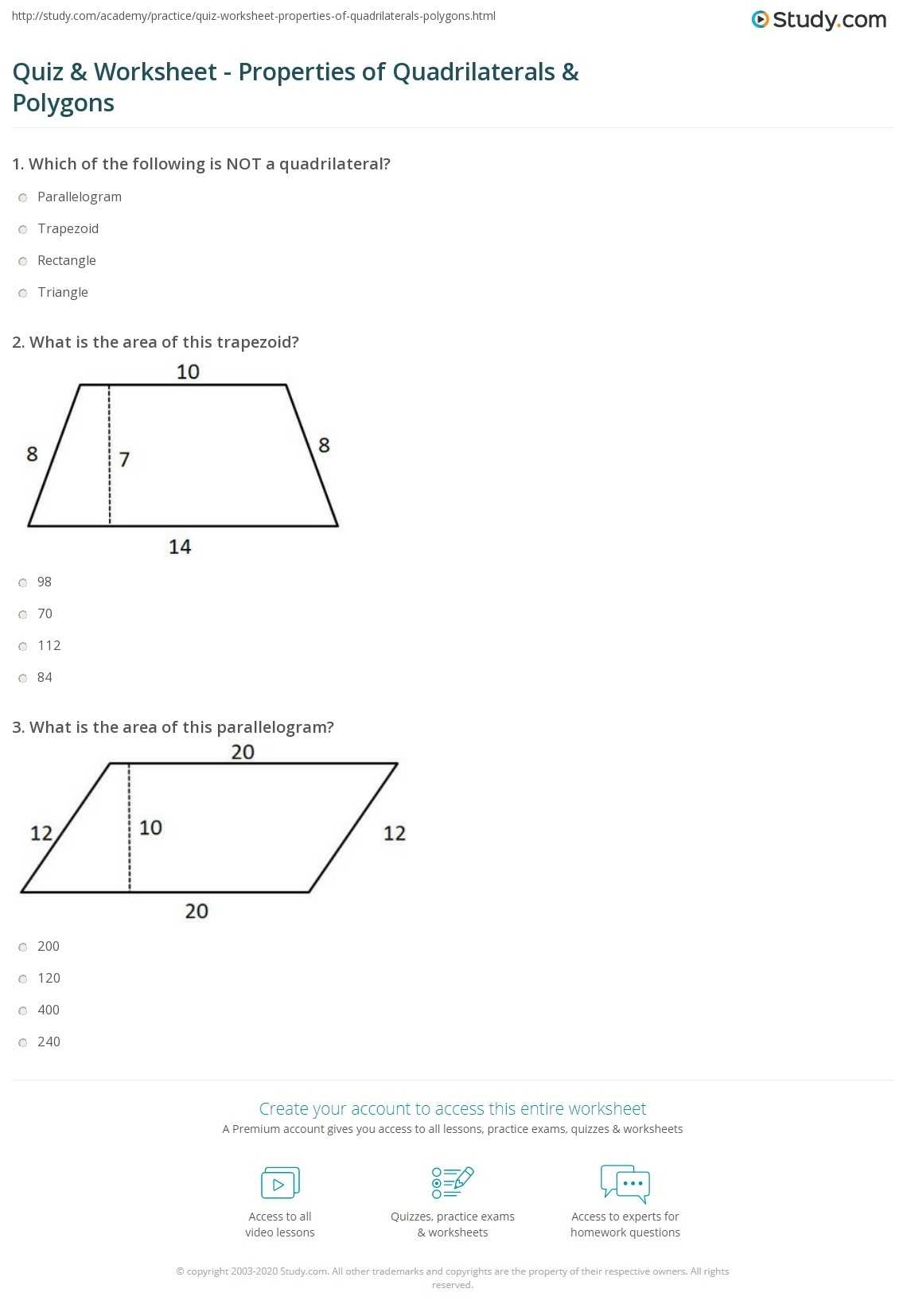
In addition, visual representation can be used to calculate the area and perimeter of a quadrilateral. By drawing a diagram and labeling the sides, one can easily calculate the perimeter of a quadrilateral. Similarly, a formula can be used to calculate the area of a quadrilateral based on the measurements of its sides.

Overall, visual representation is a helpful tool for analyzing the properties of a quadrilateral. By using diagrams, formulas, and other visual tools, one can quickly and accurately determine the type, angles, sides, diagonals, area, and perimeter of a quadrilateral.

Using Properties of Quadrilaterals Worksheets to Develop Problem-Solving Skills

Properties of quadrilaterals worksheets can be an effective way to develop problem-solving skills in students. These worksheets provide an opportunity for students to practice and apply their knowledge of the properties of quadrilaterals. By completing these worksheets, students will gain a greater understanding of how the different sides, angles and measurements of a quadrilateral can be used to make predictions and solve problems.

The worksheets can be used to introduce students to the concept of the properties of quadrilaterals and to reinforce knowledge already acquired. They can cover basic concepts such as the definition of a quadrilateral, the different types of quadrilaterals, the properties of the sides, angles and measurements of a quadrilateral, and the ability to identify a quadrilateral given a set of measurements. Students can also practice using the properties of a quadrilateral to solve problems, such as determining the area or perimeter of a quadrilateral, or finding the missing angle.

By completing these worksheets, students will gain important problem-solving skills. They will learn how to identify the properties of a quadrilateral, how to apply these properties to solve problems, and how to use the properties to make predictions. This can be a valuable skill in mathematics, science, and other problem-solving situations.

In addition to helping students develop problem-solving skills, properties of quadrilaterals worksheets can also be used to assess student knowledge and progress. By analyzing the results of the worksheets, teachers can identify which concepts need to be reviewed and which should be reinforced. This can help ensure that students are mastering the material and that they are ready to move on to more complex topics.

Overall, properties of quadrilaterals worksheets can be an effective way to develop problem-solving skills in students. These worksheets can provide an opportunity for students to practice and apply their knowledge of the properties of quadrilaterals, as well as to assess student knowledge and progress. By completing these worksheets, students will gain important problem-solving skills that can be used in mathematics, science, and other problem-solving situations.

Conclusion

The properties of quadrilaterals worksheet is a great resource for students to learn the essential properties of this important shape. It provides an in-depth look at the different types of quadrilaterals, their properties, and how to identify them. By using this worksheet, students can gain a deeper understanding of the properties of quadrilaterals and how to use them in their own problem-solving tasks. With this knowledge, students can better appreciate the fundamental importance of quadrilaterals in mathematics, and can apply their knowledge in other areas of study.