Introducing Prime Factorization Trees: A Comprehensive Guide

Prime Factorization Trees are a powerful tool for simplifying and solving complicated mathematical equations. They are a visual representation of the prime factorization of a number, and can be used to easily identify the prime factors of a number and their corresponding powers.

Prime factorization is the process of breaking down a composite number into its prime factors, which are the prime numbers that, when multiplied together, equal the original composite number. Prime factorization trees provide a visual representation of this process, making it easier to understand and solve equations involving prime numbers.

A prime factorization tree is composed of several nodes, or circles, connected by lines. Each node represents a prime factor, and the lines connecting them represent the powers of each prime factor. The lowest node is the prime factor with the highest power, and the highest node is the prime factor with the lowest power. The length of the line connecting two nodes indicates the power of the prime factor represented by the lower node.

To find the prime factorization of a number, begin by finding the smallest prime factor of the number. Place this prime factor in the lowest node of the tree. Then, divide the original number by the prime factor, and place the resulting number in the node above. Continue this process until the resulting number is 1.

For example, to find the prime factorization of 20, start by finding the smallest prime factor of 20, which is 2. Place 2 in the lowest node of the tree. Then, divide 20 by 2, which is 10. Place 10 in the node above. Divide 10 by 2, which is 5. Place 5 in the node above. Divide 5 by 5, which is 1. Place 1 in the node above. The prime factorization of 20 is 2*2*5.

Prime factorization trees can also be used to solve equations involving prime numbers. To do this, begin by finding the prime factorization of each number in the equation. Then, create a tree for each prime factorization. Compare the trees, and identify any common prime factors and their corresponding powers. Multiply these common prime factors together, and subtract their corresponding powers from each side of the equation.

For example, to solve the equation 4x^2 = 16, start by finding the prime factorization of 4 and 16. 4 = 2*2 and 16 = 2*2*2*2. Create a tree for each prime factorization. Notice that each tree has a common prime factor, 2. Multiply 2*2 together to get 4, and subtract the corresponding powers (2 and 2) from each side of the equation. The equation then becomes x^2 = 4. Divide both sides by 4 to get x^2 = 1. The solution is x = 1.

Prime Factorization Trees are a powerful tool for simplifying and solving complicated equations. With a little practice, they can help make math easier, and more enjoyable.

Exploring the Benefits of Using Prime Factorization Trees in the Classroom

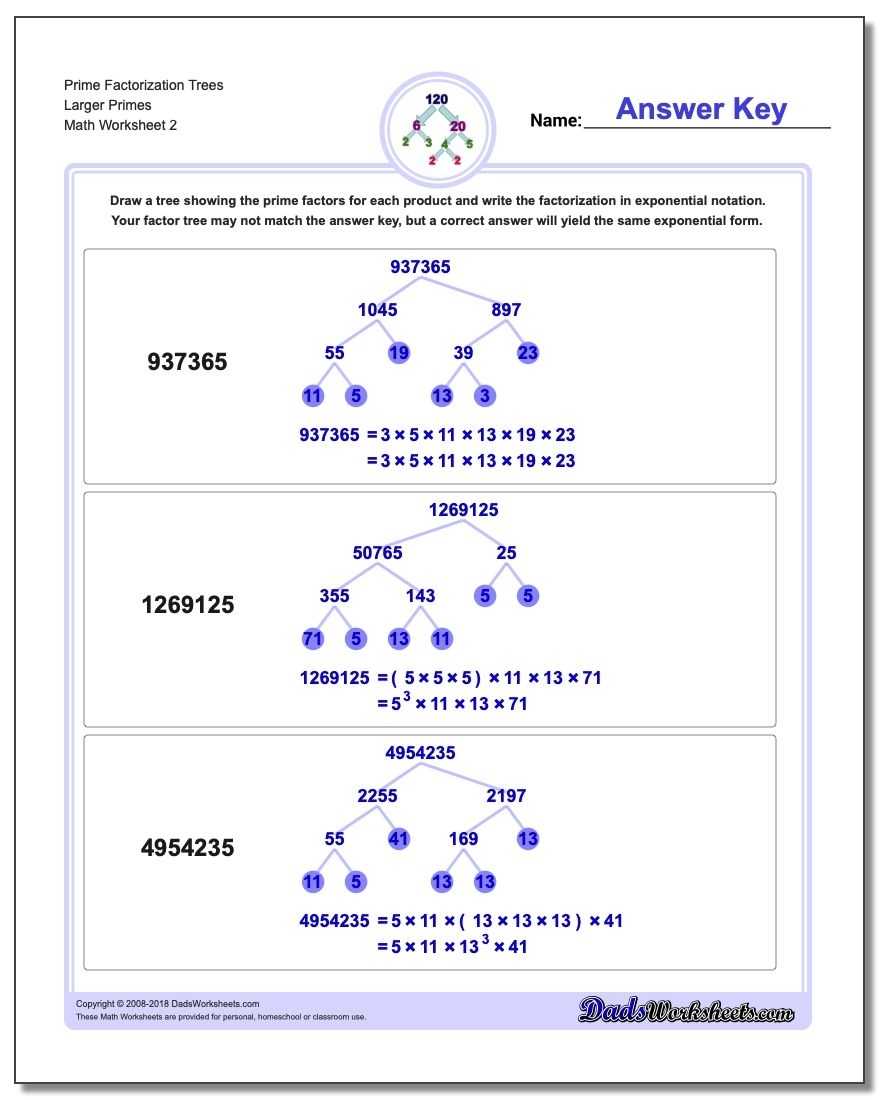
Prime factorization trees are a useful tool for teaching students how to find the prime factors of a number in a visual way. The method has been used in classrooms around the world to help students understand the concept of prime numbers.

A prime factorization tree is a diagram that helps students visualize the decomposition of a composite number into its prime factors. It is a graphical representation of prime factorization, which is the process of breaking down a number into its smallest prime factors. The tree is arranged so that the root of the tree is the composite number, and each branch represents a factor of the number. For example, if the number is 24, the root of the tree is 24 and the branches will represent the factors 2, 3, and 4.

Using a prime factorization tree in the classroom has several benefits. Firstly, it helps students to better understand and remember the concept of prime numbers. By breaking down the number into its prime factors, students are able to easily see the different factors and how they contribute to the total number. This helps them to remember the concept and makes it easier for them to solve math problems.

Secondly, using a prime factorization tree in the classroom gives students a visual representation of the math they are learning. By providing a diagram, students are able to better understand the concept and are more likely to remember it in the future. This can be especially helpful for those students who are visual learners, as they will be able to more easily understand the concept.

Finally, using a prime factorization tree in the classroom can be a fun and engaging way for students to learn about prime numbers. By providing a visual representation, students are able to explore the concept in a more interactive way. This can make learning more exciting and help students stay engaged in the lesson.

In conclusion, using prime factorization trees in the classroom can be a great way to help students understand the concept of prime numbers. It provides a visual representation that can help students remember the concept and can be an engaging and fun way for them to learn.

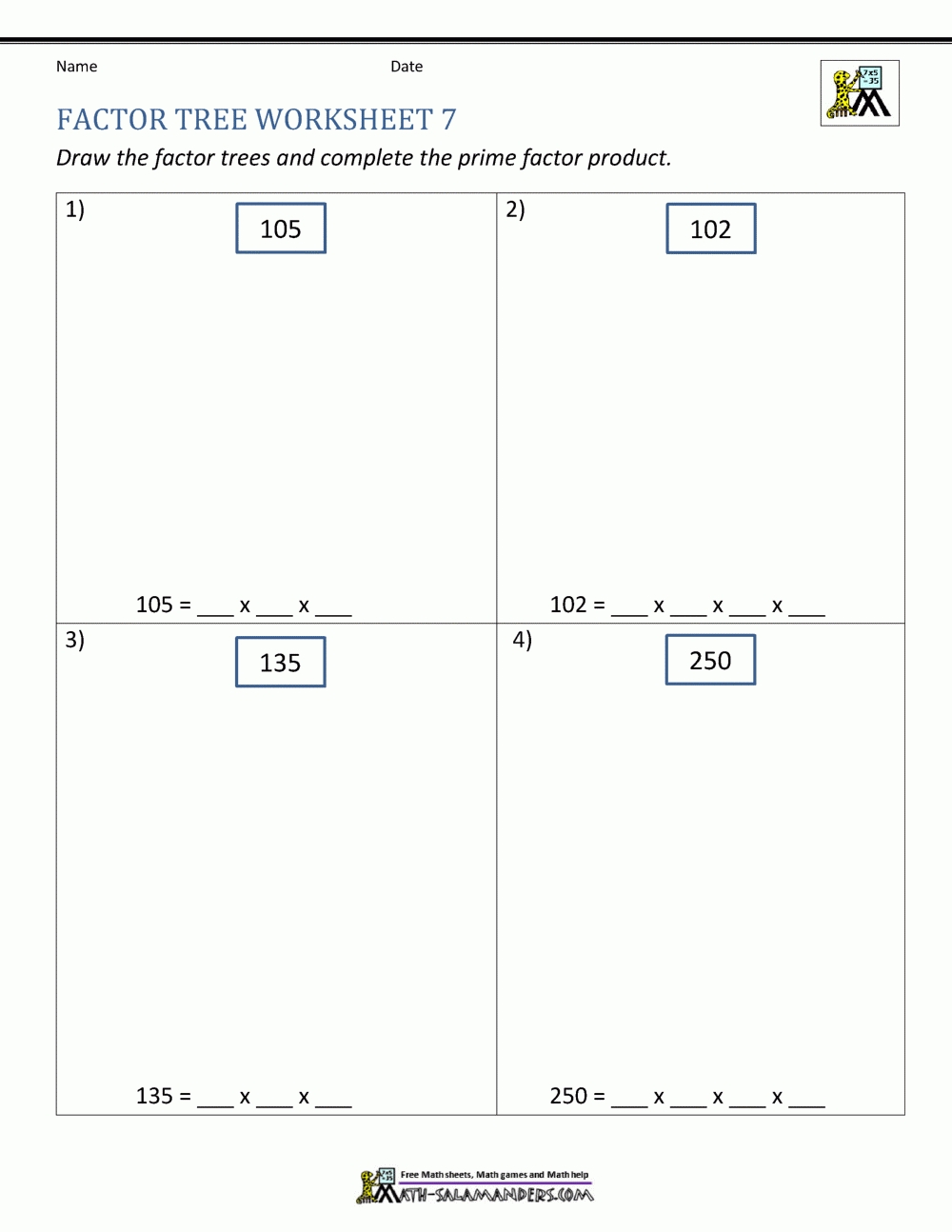
How to Use a Prime Factorization Tree Worksheet to Help Students Understand Factors and Multiples

Using a prime factorization tree worksheet is an effective way to help students understand the concepts of factors and multiples. The worksheet is designed to help students identify and identify prime numbers, as well as to calculate the prime factorization of a number.

To use a prime factorization tree worksheet, the student should begin by writing the number to be factorized on the left side of the worksheet. Then, the student should draw a vertical line down the center of the worksheet, with the number at the top. The student should then draw horizontal lines across the worksheet to create a tree-like structure.

On the left side of the tree, the student should draw the factors of the number. The student should then draw plus and minus signs to indicate whether the factor is a multiple or a factor of the number. On the right side of the tree, the student should draw the prime factors of the number.

After the student has completed the tree, they should then use a calculator to calculate the prime factorization of the number. To do this, the student should enter the number into the calculator and then calculate the prime factors of the number. The student should then enter the prime factors into the worksheet and then draw a circle around each prime factor.

Finally, the student should draw a line from each factor to the number at the top of the worksheet. By doing this, the student will be able to see the relationships between the factors and the number. This helps the student to understand the concepts of factors and multiples and can be used to help them understand other mathematical concepts.

Conclusion

The Prime Factorization Tree Worksheet is an excellent tool for helping students understand how to factor numbers. It helps students develop an understanding of how to break a number down into its prime factors. The worksheet also serves as a helpful reminder of the process and can help keep students on track when solving problems. By using this worksheet, students will gain a better understanding of prime factorization and will be better equipped to solve challenging math problems.