Analyzing the Solutions of a Points Of Concurrency Worksheet: Exploring the Different Strategies

When analyzing the solutions of a points of concurrency worksheet, it is important to consider the various strategies that can be used to solve the problem. These strategies can include solving the problem using the properties of a circle, using the properties of a triangle, and using the properties of a quadrilateral.

To solve a problem using the properties of a circle, one must first identify the center of the circle. The center of a circle is the point in which all points on the circle are equidistant from it. Once the center is identified, one can draw the radius of the circle and use the equation of a circle to determine the equation of the circle.

When solving a problem with the properties of a triangle, one must first identify the three vertexes of the triangle. Once the vertexes are identified, one can use the properties of a triangle to determine the equation of the triangle.

Finally, when solving a problem with the properties of a quadrilateral, one must first identify the four vertexes of the quadrilateral. Once the vertexes are identified, one can use the properties of a quadrilateral to determine the equation of the quadrilateral.

By using these strategies to analyze the solutions of a points of concurrency worksheet, one can understand the various ways in which a problem can be solved. By exploring these different strategies, one can gain a better understanding of the different ways in which a points of concurrency problem can be solved.

Exploring the Benefits of Understanding Points Of Concurrency Worksheet Answers

The understanding of points of concurrency is an important tool for many mathematicians and engineers. Points of concurrency are the points where three or more lines intersect, creating a single point. Understanding this concept can be beneficial for a variety of reasons.

First, points of concurrency can help mathematicians and engineers to better analyze and solve problems. Points of concurrency can provide insight into the relative positions and angles of lines, allowing for better visualization of the problem. This can be especially helpful for complex problems which involve multiple lines. Knowing where the lines intersect and the angles of the lines can help to simplify the problem, making it easier to solve.

Second, understanding points of concurrency can help engineers to create more accurate models and simulations. This is especially true for engineering projects which require precise measurements and calculations. By knowing the exact location of points of concurrency, engineers can better calculate the angles and lengths of lines, leading to more accurate models.

Third, understanding points of concurrency can help mathematicians and engineers to create more efficient algorithms. By knowing the exact location of points of concurrency, mathematicians and engineers can more efficiently process data, leading to faster computations and improved performance.

Finally, understanding points of concurrency can help mathematicians and engineers to better visualize their work. By being able to visualize the exact location of points of concurrency, it is easier to create diagrams and images of the problem. This can be very helpful for teaching and explaining the concept to others.

Overall, understanding points of concurrency is an important tool for mathematicians and engineers. It can help to simplify problems, create accurate models, create efficient algorithms, and visualize the problem. As such, understanding points of concurrency is a valuable tool for anyone working in the field of mathematics or engineering.

Identifying the Challenges of Working with Points Of Concurrency Worksheet Answers

The use of points of concurrency in mathematics can present a number of challenges for those working with them. First, there is the issue of accuracy in plotting the points. Depending on the level of precision required, plotting them can be a difficult task, as it is important that the points be placed accurately in order to represent the data accurately.

Second, there is a challenge in understanding the meaning of the points. Points of concurrency are often used to represent relationships between data points, and it is important to be able to interpret these relationships accurately. This can be a difficult task, as it often requires a deep understanding of the mathematics behind them.

Third, there is the challenge of determining the best way to represent the points. Depending on the data being represented, different methods of representing the points may be required. This can be a difficult task, as it requires an understanding of the data and the mathematics involved.

Finally, there is the challenge of applying the mathematics to the data. This can be a difficult task, as it requires an understanding of the mathematics and the data, as well as the ability to apply the mathematics to the data.

Overall, working with points of concurrency can be a challenging task. It requires an understanding of the mathematics and the data, as well as the ability to accurately plot them and interpret the relationships between the points. It also requires the ability to determine the best way to represent the points and to apply the mathematics to the data.

Comparing and Contrasting Points Of Concurrency Worksheet Answers to Other Geometry Problems

Comparing and Contrasting Points of Concurrency

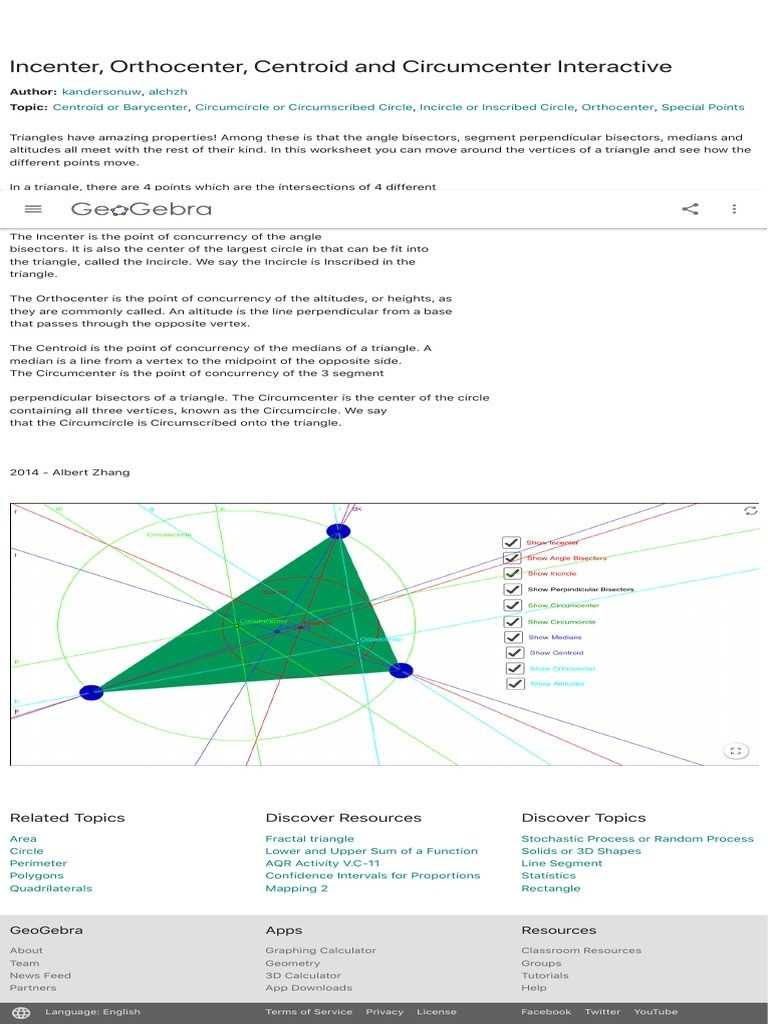
Points of concurrency are geometric points where three or more lines intersect. In geometry, there are three main types of points of concurrency: the vertex of an angle, the centroid of a triangle, and the circumcenter of a triangle. All three of these points are located in different ways, and each has different properties.

The vertex of an angle is the point where two lines meet to form an angle. It is determined by the intersection of the two lines, and can be found by drawing the lines that form the angle and measuring the angle.

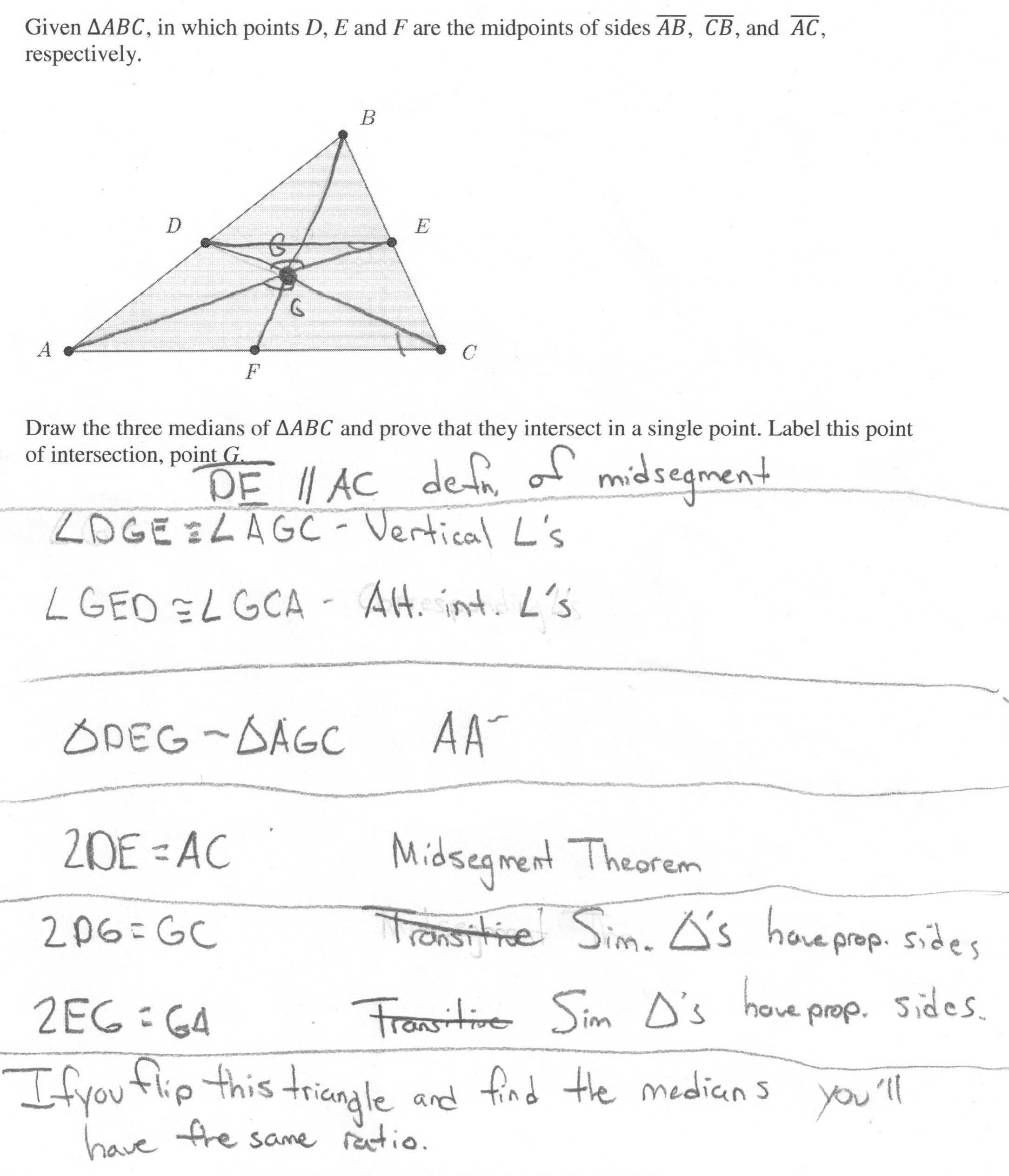
The centroid of a triangle is the point at which all three sides of the triangle meet. It is determined by taking the average of the three vertices of the triangle. The centroid is found at the intersection of the medians of the three sides of the triangle.

The circumcenter of a triangle is the point of intersection of the three perpendicular bisectors of the triangle. It is determined by taking the midpoints of each side of the triangle and connecting them. The circumcenter is found at the intersection of the three bisectors.

These three points of concurrency have different properties and uses in geometry. For example, the vertex of an angle can be used to find the measure of the angle, while the centroid and circumcenter can be used to find the area of a triangle. Furthermore, the centroid and circumcenter can be used to identify the center of a triangle, while the vertex of an angle cannot.

In conclusion, the three main types of points of concurrency in geometry are the vertex of an angle, the centroid of a triangle, and the circumcenter of a triangle. Each of these points is located in a different way, and each has different properties. The vertex of an angle can be used to find the measure of the angle, while the centroid and circumcenter can be used to find the area of a triangle and to identify the center of a triangle.

Conclusion

The Points of Concurrency Worksheet Answers provides a great resource for students to understand the concepts of points of concurrency. Through solving the problems included in the worksheet, students can gain a better understanding of the properties of points of concurrency and how they can be applied to real life situations. With the help of this worksheet, students can learn to identify and analyze points of concurrency in any given situation.