Exploring Piecewise Functions: A Comprehensive Guide to Solving Piecewise Functions Worksheets

The concept of a piecewise function can be a difficult one for students to understand. That’s why it’s important for educators to provide students with comprehensive and thorough instruction on how to solve piecewise functions worksheets. This guide will provide an overview of the topic, a step-by-step approach to solving piecewise functions worksheets, and tips to help students succeed.

At the core of solving piecewise functions worksheets lies the notion of a piecewise function. A piecewise function is a function that is broken into pieces, each of which is defined by its own formula. Each piece of the function is usually defined by a different equation, and the points at which the equations change are called breakpoints.

To solve piecewise functions worksheets, students must first identify all the breakpoints. This can be done by looking for points at which the equation changes, or by finding the x-intercepts of the equations. Once all the breakpoints have been identified, students should write down the equations and determine the domain and range of the function.

The next step in solving piecewise functions worksheets is to graph the equations. Students should graph each equation on a coordinate plane, labeling each point on the graph with its corresponding equation. Once the graphs have been drawn, students will be able to identify each piece of the function, as well as the breakpoints that separate them.

The final step in solving piecewise functions worksheets is to substitute the breakpoints into the equations and find the values of the function at each breakpoint. Students should use the formulas to calculate the values at each breakpoint, and then use the values to determine the overall shape of the function. This process is repeated until all the breakpoints have been evaluated.

By following these steps and demonstrating a thorough understanding of the material, students can gain a better grasp of the concept of piecewise functions. With practice, students will eventually be able to solve the more complex piecewise functions worksheets with ease. Furthermore, by understanding the concepts behind piecewise functions, students will be able to apply what they’ve learned to other mathematical problems.

A Step-by-Step Breakdown of How to Use Piecewise Functions Worksheet With Answers

Piecewise functions are a type of function that can be used to describe different behaviors of a function based on certain conditions. They are very useful in solving a wide range of problems and can be used to model real-world scenarios. This worksheet will provide a step-by-step breakdown of how to use piecewise functions, complete with answers.

Step 1: Understand the concept of piecewise functions.

A piecewise function is a function that is defined by different parts or pieces over certain intervals. This means that the behavior of the function changes depending on the domain or range of the values of the independent variable. For example, a piecewise function can have different expressions depending on whether the value of the independent variable is between 0 and 10, or between 11 and 20.

Step 2: Identify the different parts or pieces of the piecewise function.

When using a piecewise function, it is important to identify the different parts or pieces of the function. Each part or piece should be labeled in order to distinguish one from the other. For example, if the piecewise function is defined by two different expressions, one for when the independent variable is between 0 and 10 and another for when the independent variable is between 11 and 20, the two parts should be labeled as “Part 1” and “Part 2”, respectively.

Step 3: Express each part or piece of the piecewise function as an equation.

Once the different parts or pieces of the piecewise function have been identified, each part should be expressed as an equation. To do this, the independent and dependent variables should be identified and the equation should be written in terms of these variables. For example, if the independent variable is x and the dependent variable is y, the equation for Part 1 of a piecewise function might be expressed as y = 3x + 2.

Step 4: State the conditions for each part or piece of the piecewise function.

Once the equations for each part or piece of the piecewise function have been written, the conditions for each part should be stated. These conditions should specify the range of values for the independent variable for which each equation is valid. For example, the conditions for Part 1 of the piecewise function might be stated as “for 0 ≤ x ≤ 10”.

Step 5: Express the piecewise function as one equation.

Finally, the piecewise function should be expressed as one equation. To do this, the equations for each part or piece should be combined and the conditions should be included. For example, the equation for the piecewise function discussed above might be expressed as y = 3x + 2 for 0 ≤ x ≤ 10 and y = 5x + 4 for 11 ≤ x ≤ 20.

By following the steps outlined above, you should now have a better understanding of how to use piecewise functions. By identifying the different parts or pieces of a piecewise function, expressing each part as an equation, and combining them into one equation, you can use piecewise functions to model real-world scenarios and solve a variety of problems.

Unpacking the Different Types of Piecewise Functions and How to Solve Them

Piecewise functions are mathematical expressions that are made up of two or more distinct parts, known as pieces. Each piece is defined by a formula and a set of conditions. By graphing these pieces separately, it is possible to visualize the behavior of the function. Piecewise functions are useful for modeling situations where the output of a function changes based on the value of the input.

There are three different types of piecewise functions. The first type is the absolute value function, which is defined by two pieces: one for positive inputs and one for negative inputs. The second type is the step function, which is composed of two or more pieces that are connected by vertical lines. The third type is the piecewise linear function, which consists of two or more linear pieces that are connected by horizontal lines.

To solve a piecewise function, the first step is to find the values of the independent variable that define the boundaries between the pieces. These values are known as breakpoints. Once the breakpoints have been identified, the piecewise function can be expressed in the form of a piecewise equation, which consists of multiple equations connected by logical operators.

From there, the piecewise equation can be solved using the same methods used to solve other types of equations. The solution will depend on the type of function and the given breakpoints. For example, to solve an absolute value function, the equation must be split into two equations, one for positive inputs and one for negative inputs. The equations can then be solved using substitution or factoring.

For step or piecewise linear functions, the solution can be found using the slope-intercept form, which involves solving for the slope and y-intercept of each line segment. Finally, a graph can be created of the piecewise function to show how the output changes depending on the input. This can be useful for visualizing the behavior of the function and for identifying special points such as local maxima or minima.

How to Master the Art of Solving Piecewise Functions Problems With Answers

Solving piecewise functions problems is an important skill for students to master. Piecewise functions are functions composed of two or more equations that are used to define different functions for different domains. Understanding how to solve these types of problems can help students develop deeper insight into mathematical concepts and improve their problem-solving skills.

To begin, it is important to understand the definition of a piecewise function. A piecewise function is a function that is defined by different equations on different intervals. Each interval is referred to as a “piece” and the equations that define the function on that piece are referred to as “pieces” of the function. The domain of a piecewise function is the set of values for which the function is defined.

Once you understand the definition of a piecewise function, you can begin to solve problems involving these functions. To do this, you must first identify the different pieces and then determine the equations that define each piece. You must then solve each equation and graph the function to see how the pieces fit together.

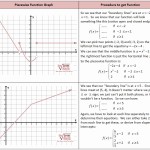
To illustrate, consider the following piecewise function:

F(x) =
{ 2x + 1 , x < 0 { x^2 , 0 ≤ x < 1 { 3x – 1 , x ≥ 1 To solve this problem, you must first identify the different pieces. In this case, there are three pieces: one for x < 0, one for 0 ≤ x < 1, and one for x ≥ 1. You must then determine the equations that define each piece. In this example, the equations are 2x + 1 for x < 0, x^2 for 0 ≤ x < 1, and 3x – 1 for x ≥ 1. Once you have identified the equations and the domain for each piece, you can solve the equations and graph the function. To solve the equations, you must substitute the given values for x into each equation and solve for y. In this example, this yields y = 2x + 1 for x < 0, y = x^2 for 0 ≤ x < 1, and y = 3x – 1 for x ≥ 1. To graph the function, you must plot the points that are created from solving each equation. In this example, the points would be (0, 1), (1, 0), and (2, 5). Once all of the points have been plotted, you can connect them to create the graph of the piecewise function. By mastering the art of solving piecewise functions problems, students can develop a better understanding of mathematical concepts and improve their problem-solving skills. It is important to understand the definition of a piecewise function and to be able to identify and solve each piece of the function. Additionally, it is important to be able to graph the function in order to see how the pieces of the function fit together. With practice, students can master this important skill and become more successful in their mathematical studies.

Using Piecewise Functions to Solve Real-World Problems: A Comprehensive Guide

Piecewise functions are one of the most powerful mathematical tools available for solving real-world problems. They are a type of function that divides the domain into multiple intervals and then assigns a different expression for each interval. Piecewise functions allow for the determination of complex relationships between inputs and outputs that are not easily achievable with other types of functions. This guide will provide a comprehensive overview of the fundamentals of working with piecewise functions and demonstrate how they can be used to solve real-world problems.

To start, it is important to understand the basic components of a piecewise function. A piecewise function is composed of two distinct parts: the intervals, and the expressions associated with those intervals. The intervals are the sections of the domain in which the piecewise function will be evaluated, while the expressions associated with those intervals are the equations that determine the output of the function within that interval.

When constructing a piecewise function, it is important to consider the continuity of the function. A piecewise function is considered continuous when the right-hand limit of the expression associated with one interval is equal to the left-hand limit of the expression associated with the next interval. This ensures that the output of the function is continuous throughout the domain.

Once a piecewise function is constructed, it can then be used to solve real-world problems. The most common application is to determine the output of the function for a given input. To do this, the input must be evaluated against the intervals of the piecewise function to determine which expression should be used. Once the expression has been identified, the output can be calculated using the appropriate equation.

In addition to evaluating the output of a piecewise function for a given input, it is also possible to use piecewise functions to solve optimization problems. This is done by identifying the interval containing the optimal value and then solving the associated equation to determine the optimal input.

Piecewise functions can also be used to solve calculus problems such as finding derivatives and integrals. For example, a piecewise function can be used to calculate the area under a curve by identifying the intervals and then calculating the area of each section.

Finally, piecewise functions can be used to graphically represent data. This is done by plotting each expression associated with an interval on a graph with the appropriate domain and range. This can be used to visualize relationships between inputs and outputs in a way that is not readily achievable with other types of functions.

In conclusion, piecewise functions are an invaluable tool for solving real-world problems. They allow for the determination of complex relationships between inputs and outputs, and can be used for a variety of applications such as evaluating outputs, solving optimization problems, calculating derivatives and integrals, and graphically representing data. With a basic understanding of the fundamentals of working with piecewise functions, it is possible to use them to solve a variety of real-world problems.

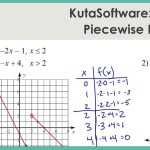
Understanding Piecewise Functions: A Comprehensive Guide to Piecewise Functions Worksheets With Answers

Piecewise functions are a type of mathematical function in which two or more equations are joined at certain values of the independent variable. They are used to represent functions with discontinuous behavior, such as those for which the derivative does not exist at certain points. Piecewise functions are often seen in calculus and other advanced mathematics courses.

Understanding piecewise functions can be challenging, but there are many resources available to help students learn and practice their skills. Worksheets with answers can be an excellent way for students to practice their understanding of piecewise functions. With worksheets, students can work through problems and check their answers, reinforcing the concepts in the process.

Worksheets with answers for piecewise functions typically begin with a description of how to identify and work with piecewise functions. They may then provide specific examples of piecewise functions and how to evaluate them using the given equations. The worksheets may also provide step-by-step instructions for solving or graphing a piecewise function.

In addition to providing answers to the worksheets, students can practice their skills by solving piecewise functions on their own. This can help them develop a deeper understanding of the concepts and apply them in other areas.

Overall, worksheets with answers can be a great way for students to develop their understanding of piecewise functions. With practice and guidance from the worksheets, students can build a strong foundation for more advanced math courses.

The Benefits of Using Piecewise Functions to Teach Math: Understanding When to Use Piecewise Functions Worksheets With Answers

Piecewise functions are an essential tool in teaching mathematics, as they provide students with the opportunity to learn and apply a wide variety of mathematical concepts. By using piecewise functions, students are able to develop an understanding of the relationships between different functions, as well as the importance of considering the domain and range of a given function.

By using piecewise functions, students can learn to graph a variety of functions, such as step functions and absolute values, and to solve problems involving piecewise functions. Piecewise functions can also be used to teach various topics in algebra, such as linear equations, inequalities, and systems of equations. Piecewise functions can also be used to develop an understanding of calculus and its various topics, such as derivatives and integrals.

Using piecewise functions worksheets with answers can help students develop their understanding of the concepts involved in the use of piecewise functions. These worksheets provide students with the opportunity to practice and apply the concepts they learn with the help of sample problems and solutions. The worksheets also provide students with the opportunity to check their own understanding and to assess their progress in learning about piecewise functions.

By using worksheets with answers, students can gain insight into the different types of piecewise functions, their properties, and the ways in which they can be used to solve various types of equations. This can help students become more confident in their ability to solve the equations they encounter in their math classes.

In addition, using worksheets with answers can help students understand when to use piecewise functions, as well as the types of problems that require the use of piecewise functions. This can help students better understand the importance of considering the domain and range of a given function, as well as the different ways in which these functions can be used to solve different types of equations.

Overall, using piecewise functions worksheets with answers can provide a valuable learning opportunity for students who wish to gain a better understanding of how piecewise functions can be used in mathematics. These worksheets can help students develop an understanding of the various types of functions, as well as the different ways in which they can be used to solve various types of equations. Additionally, these worksheets can help students develop the necessary skills to become better problem-solvers and mathematicians.

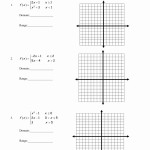
Tips for Solving Complex Piecewise Functions Worksheets With Answers

1. Begin by reading the entire worksheet. Carefully note all of the instructions given, as well as which pieces of the puzzle are provided and which are not. Pay attention to the various variables, coefficients, and constants that are involved in the given problem.

2. Break the problem into manageable pieces. If there are multiple steps involved, it can be helpful to break the problem down into smaller chunks and tackle them one at a time.

3. Utilize the given information. Use the given information to determine what type of equation or function is being asked for. This can help to narrow down the possible solutions and make the problem more manageable.

4. Analyze the graph. If a graph is provided, it can be helpful to analyze the graph and compare it to the given information. This can help to identify any patterns or trends that may exist in the given problem.

5. Make an educated guess. If the given information does not provide enough information to solve the problem, it can be helpful to make an educated guess and see if the answer works. This can help to narrow down possible solutions and save time.

6. Double check the answer. After arriving at a solution, double check the answer to make sure it is correct. This can help to ensure that the problem is solved correctly and that the solution is valid.

Exploring Piecewise Functions in Different Contexts: A Guide to Piecewise Functions Worksheets With Answers

Piecewise functions are mathematical expressions that are composed of multiple pieces, each of which is defined over a different domain. These functions can be used to model a wide variety of phenomena, from financial data to physical motion. Piecewise functions offer an efficient way to analyze and understand complex systems.

In this guide, we will explore the concept of piecewise functions, discuss how they are used in different contexts, and provide a variety of worksheets with answers that will help readers understand and apply the concepts.

To begin, let us define a piecewise function. A piecewise function is a function that is composed of multiple pieces, each of which is defined over a different domain. Each piece of the function is defined by a separate equation, and the entire function can usually be expressed as an equation that is composed of the individual pieces.

Piecewise functions are useful in many different contexts. For example, they can be used to model financial data, to model physical motion, or to solve differential equations. In addition, they can be used to analyze complex systems, such as networks or biological systems.

In addition to their uses in modeling, piecewise functions can also be used to calculate numerical values. This is particularly useful when calculating derivatives or integrals. By using piecewise functions, it is possible to calculate numerical values quickly and accurately.

Now that we have discussed the concept of piecewise functions, let us move on to discussing how they are used in different contexts. Financial data is often modeled by piecewise functions, as they can be used to capture the dynamics of market movements. Physical motion can also be modeled by piecewise functions, as they can provide an efficient way to describe the motion of objects. In addition, piecewise functions can be used to solve differential equations, as they can provide an efficient way to solve problems involving derivatives or integrals.

Finally, let us discuss the worksheets provided in this guide. The worksheets are designed to help readers understand and apply the concepts discussed in this guide. Each worksheet has a corresponding answer key that provides detailed explanations and examples. By working through the worksheets, readers will be able to gain a better understanding of the concept of piecewise functions, as well as how they can be used in different contexts.

In conclusion, piecewise functions offer an efficient way to model and analyze complex systems. This guide provides an overview of the concept of piecewise functions, as well as how they are used in different contexts. It also provides a variety of worksheets with answers that will help readers understand and apply the concepts. By working through the worksheets, readers will gain a better understanding of the concept of piecewise functions and how they can be used in different contexts.

Challenges and Rewards of Working With Piecewise Functions Worksheet With Answers

Working with piecewise functions can be both challenging and rewarding. Piecewise functions are functions that are defined differently over different intervals of the domain. They are often used to precisely model phenomena that vary over time or space.

The challenge of working with piecewise functions lies in the intricacy of the function’s definition. Each piecewise function is composed of multiple distinct parts, each with its own distinct input and output values. This means that each piece of the function must be evaluated separately in order to obtain the full output value. This can make it difficult to visualize the overall behavior of the function or to work with it without making mistakes.

However, the rewards of working with piecewise functions are also considerable. Piecewise functions can be used to model many real-world phenomena that may otherwise be difficult or impossible to describe with a single function. They allow us to precisely capture the nuances of these phenomena, which can be valuable for analysis and prediction. Additionally, they can provide a more accurate description of a phenomenon than a single function could, allowing us to make more informed decisions.

Overall, working with piecewise functions can be both challenging and rewarding. While the complexity of their definition can make them difficult to work with, they can also be extremely useful for modeling and understanding real-world phenomena.

Conclusion

The Piecewise Functions Worksheet With Answers is a great way to learn about how to solve complex equations involving piecewise functions. It provides an easy way to understand the concepts behind piecewise functions and how to solve equations involving them. With the help of this worksheet, students can master the concepts of piecewise functions and be able to solve equations involving them with ease.