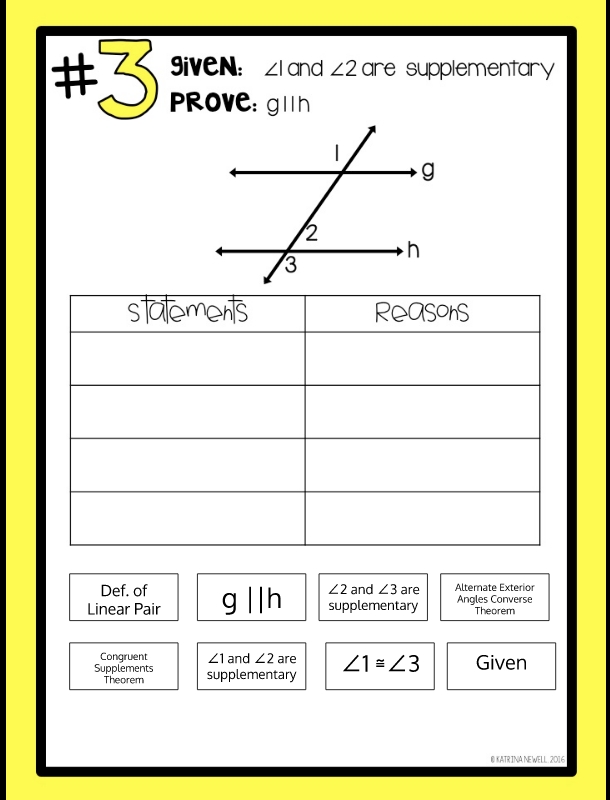
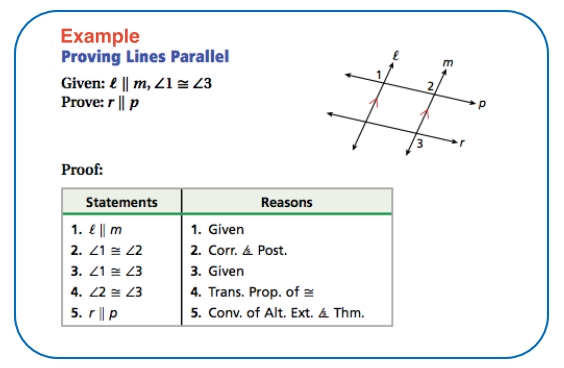
Understanding the Basics of Parallel Lines Proofs Worksheet Answers

Parallel lines proofs are an important part of geometry. In order to understand how they work, it is important to understand the basics of these proofs.

Parallel lines proofs are used to prove that two or more lines are parallel to one another. This is done by using a series of statements and reasons to form a logical argument. To be successful in proving that two lines are parallel, a student must use the concept of parallelism, geometry theorems, postulates, and properties.

The first step in a parallel lines proof is to state the given information. This includes the given lines and any other information that is necessary for the proof. This information should be organized in a way that makes it easy to refer to later on in the proof.

Once the given information has been stated, the student must then use the parallelism concept to determine if the lines meet the criteria for being parallel. This involves looking at the angles formed by the lines and the angles created by the intersections of the lines. If the angles formed by the lines are equal, then the lines are parallel.

Next, the student must use the geometry theorems, postulates, and properties to determine if the lines meet the criteria for being parallel. This involves looking at the slopes of the lines and the points where the lines cross. If the slopes of the lines are equal, then the lines are parallel.

The last step in a parallel lines proof is to state the conclusion. This is done by summarizing the evidence that has been gathered and stating that the two lines are parallel.

By understanding the basics of parallel lines proofs, students can more easily understand how to prove that two lines are parallel. They can then use this understanding to solve more complex problems related to parallelism.

Exploring Creative Ways to Explain Parallel Lines Proofs Worksheet Answers

Parallel lines proofs are an essential part of geometry that require a thorough understanding of the properties of parallel lines. In order to understand and be able to apply these proofs correctly, it is important to have a clear understanding of the definitions and properties of parallel lines.

The Parallel Lines Proofs Worksheet provides a helpful tool to understand the underlying principles of parallel lines proofs. The worksheet contains a series of questions, each of which requires the student to apply their knowledge of the properties of parallel lines to solve the problem.

The worksheet begins by introducing the concept of parallel lines and then goes on to explain the properties of parallel lines. It then presents a series of proofs, each of which must be completed correctly in order to properly demonstrate the student’s understanding of the properties of parallel lines. Each proof is accompanied by an explanation of the steps required to solve it, as well as a set of diagrams to help students visualize the process.

The worksheet also provides an opportunity to practice creative ways of explaining parallel lines proofs. For example, students can use a variety of metaphors and analogies to explain the properties of parallel lines. For instance, they can compare two parallel lines to two pieces of string that are tied together at one end, with the other ends stretching out in opposite directions. This analogy helps to explain how two lines that never meet are parallel.

In addition, the worksheet provides an opportunity to practice writing in a formal tone. Students can practice using technical terms and precise language to explain their proofs. This helps them to develop a deeper understanding of the concepts involved and to express their ideas clearly and accurately.

Overall, the Parallel Lines Proofs Worksheet provides an invaluable educational resource for students trying to develop a comprehensive understanding of the properties of parallel lines. By providing a range of questions and explanations, it helps students to master the fundamentals of parallel lines proofs and encourages them to think creatively about how to explain them.

Comparing Different Solutions to Parallel Lines Proofs Worksheet Answers

This worksheet provides an opportunity to compare and contrast different solutions to the same proof involving parallel lines. Each solution contains steps that demonstrate the different approaches to the problem.

The first solution begins by introducing the given information, which includes two parallel lines as well as several transversals. It then explains the concept of alternate interior angles, which can be used to prove that the parallel lines are congruent. This is followed by the use of appropriate diagrams to illustrate the concept. The proof is then completed by showing that the alternate interior angles are equal, thus proving that the two lines are parallel.

The second solution follows a similar approach, but adds the concept of corresponding angles to the proof. This concept is used to demonstrate that the two parallel lines are congruent. The proof is completed by showing that the corresponding angles are equal, thus proving that the two lines are parallel.

The third solution takes a different approach, introducing the concept of consecutive interior angles. This concept is used to show that the two lines are parallel. The proof is then completed by showing that the consecutive interior angles are equal, thus proving that the two lines are parallel.

Each of the three solutions provides a different approach to the same proof involving parallel lines. The first solution uses alternate interior angles to prove the parallel lines are congruent. The second solution adds the concept of corresponding angles to prove congruency, and the third solution uses consecutive interior angles to prove that the lines are parallel. All three solutions demonstrate the same end result, but present different methods of arriving at that result.

Conclusion

The Parallel Lines Proofs Worksheet Answers provide a great way for students to practice their knowledge of geometry and prove theorems related to parallel lines. With the right approach and practice, students can understand the concept of parallel lines and be able to prove theorems related to them. The worksheets also serve as a great way to assess the students’ understanding of the material. By practicing and understanding the material, students can gain a better understanding of how to apply the theorems to their own mathematical problems.