Understanding the Basics of Multiplying and Dividing Monomials: A Comprehensive Worksheet Guide

This comprehensive worksheet guide will provide students with the necessary skills to understand the basics of multiplying and dividing monomials. It is designed to help students develop a strong foundation of knowledge and understanding of the fundamental concepts of multiplying and dividing monomials.

Multiplying and dividing monomials are fundamental operations that are used in many areas of mathematics, such as algebra, calculus, and trigonometry. As such, it is important that students understand the basic principles underlying these operations. This worksheet guide will cover the basics of multiplying and dividing monomials, starting with the definition and terminology of monomials, and then progressing to the various methods of multiplying and dividing them.

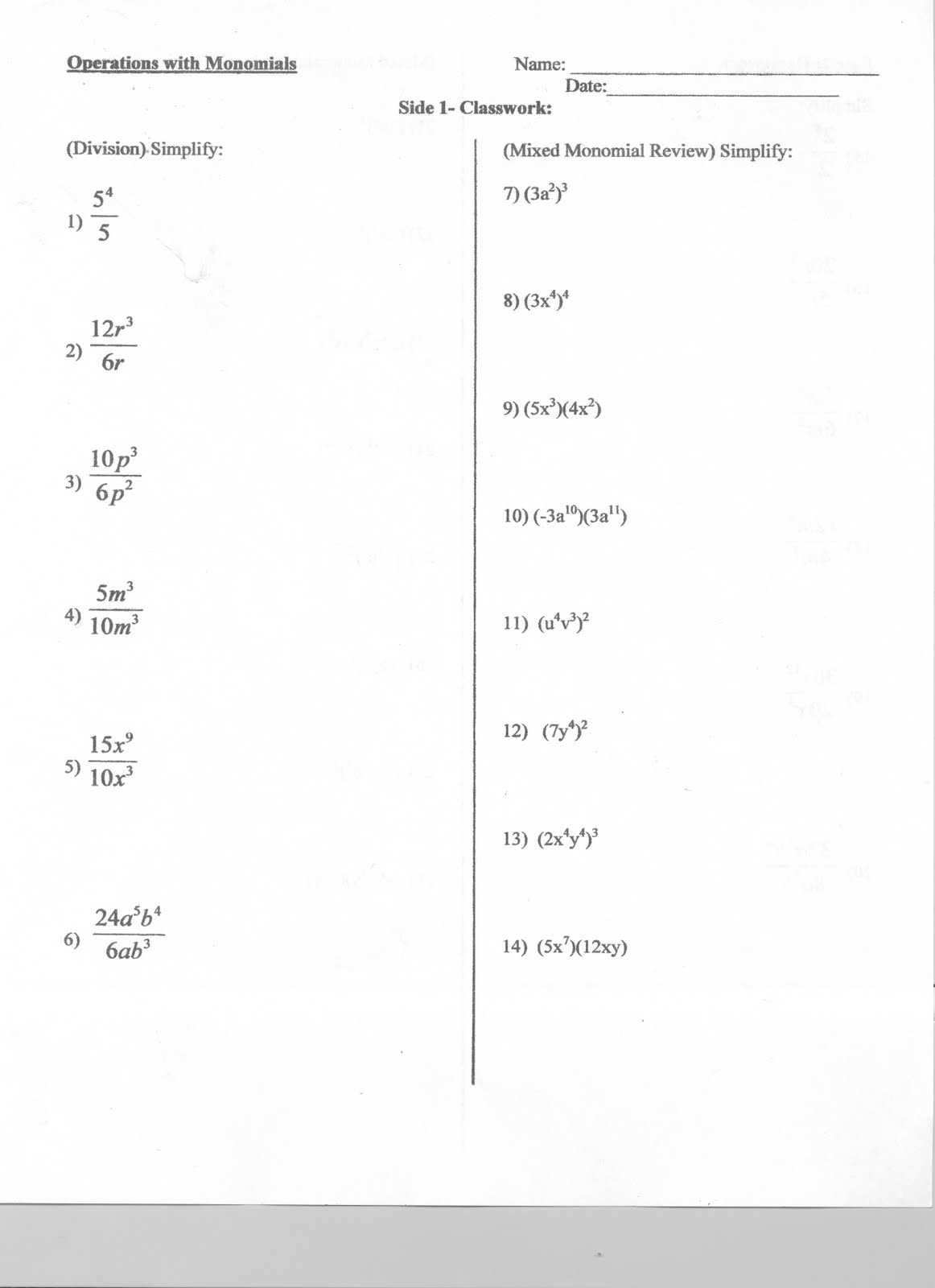
The first part of this worksheet guide will explain the definition and terminology of monomials. A monomial is simply a mathematical expression consisting of a single term. It can be of the form axn, where a is a real number and n is an integer. The terms of a monomial can be multiplied or divided by each other, resulting in a new monomial.

The next section of this worksheet guide will cover the different methods of multiplying and dividing monomials. The most common methods are the multiplication of two monomials, the division of two monomials, and the power rule. This section will also explain how to simplify monomials using the distributive property.

The last part of this worksheet guide will discuss how to use the various methods of multiplying and dividing monomials to solve equations and inequalities. This will include a review of factoring, as well as how to solve equations and inequalities with more than two terms.

This comprehensive worksheet guide will provide students with the necessary skills to understand the basics of multiplying and dividing monomials. By following the steps outlined in this guide, students will gain a strong foundation of knowledge and understanding of the fundamental concepts of multiplying and dividing monomials, and will be able to use these operations to solve equations and inequalities.

Exploring the Different Strategies for Multiplying and Dividing Monomials: A Step-by-Step Worksheet

Multiplying and dividing monomials can be a tricky process, particularly for those just starting to learn algebra. To help students get a better understanding of this important concept, this worksheet will take a step-by-step approach to exploring the different strategies for multiplying and dividing monomials.

Step One: Understand the Basics

Before attempting to multiply or divide monomials, it is important to understand the basics. Monomials are a type of algebraic expression made up of a single term. This term can be a variable, an exponent, or a combination of both.

Step Two: Multiplying Monomials

To multiply monomials, the first step is to multiply the coefficients, which are the numbers in front of each term. For example, if you were multiplying 3×2 and 5×3, you would multiply 3 and 5 to get 15. Next, you would multiply the variables, which are the parts of the expression that are not numbers. In this example, you would multiply x2 and x3 to get x5. Finally, you would combine the coefficient and variables to get your answer, 15×5.

Step Three: Dividing Monomials

Dividing monomials requires a slightly different approach. To divide monomials, you must first divide the coefficients. For example, if you were dividing 12×4 by 4×2, you would divide 12 by 4 to get 3. Then, you would divide the variables, which are the parts of the expression that are not numbers. In this example, you would divide x4 by x2 to get x2. Finally, you would combine the coefficient and variables to get your answer, 3×2.

Step Four: Practice

Now that you understand the basics of multiplying and dividing monomials, it is time to practice. Try solving a few of the following problems:

1. Multiply 4×2 and 6×7

2. Divide 9×5 by 3×2

3. Multiply 5×3 and 10×2

4. Divide 22×4 by 11×2

Answers:

1. 24×9
2. 3×3
3. 50×5
4. 2×2

Developing a Strong Understanding of Exponents through Multiplying and Dividing Monomials: A Worksheet

Developing a strong understanding of exponents is an essential part of algebra and mathematics. This worksheet provides an opportunity for students to practice and master the concept of multiplying and dividing monomials with exponents.

This worksheet is designed to help students practice and strengthen their understanding of exponents by multiplying and dividing monomials. The worksheet contains six questions that allow students to practice the skills necessary to solve equations with multiple exponents.

Each of the six questions on the worksheet requires students to calculate the product or quotient of two monomials with exponents. The questions range in difficulty from simply multiplying two monomials with the same base to multiplying two monomials with different bases and different exponents.

At the end of the worksheet, students are required to explain how their answers were determined. This enables students to reinforce their understanding of the process for multiplying and dividing monomials with exponents.

This worksheet is an excellent way for students to practice and perfect their understanding of exponents. It provides an engaging and stimulating way for students to practice the skills they will need to use when solving equations with multiple exponents.

Mastering the Concept of Multiplying and Dividing Monomials with Word Problems: A Worksheet Guide

Introduction
Multiplying and dividing monomials are basic mathematical operations that are essential for students to master. This worksheet guide will provide students with the knowledge to successfully tackle monomial multiplication and division word problems. By the end of this guide, students will be able to identify and solve monomial multiplication and division problems with ease.

What is a Monomial?
A monomial is an algebraic expression that is composed of only one term. A term is a numerical coefficient or numerical constant multiplied by a combination of variables and their exponents. For example, 2x²y, -5xy, and 7 are all monomials.

What is Multiplying Monomials?
Multiplying monomials is a process of combining like terms. Like terms are terms that have the same variables and exponents. This can be done by adding the numerical coefficients and multiplying the variables and their exponents. For example, to multiply (2x²y) and (3xy), one would add the numerical coefficients, which is 5, and multiply the variables and their exponents, which is 6x³y². The answer to this equation is 5x³y².

What is Dividing Monomials?
Dividing monomials is a process of using the inverse operation of multiplication. This is done by first determining the greatest common factor (GCF) between the two monomials. The GCF is the largest numerical coefficient or numerical constant that can be divided evenly into both monomials. The GCF is then divided from both monomials and the remaining terms are divided from each other. For example, to divide (6xy³) and (3xy), one would first identify the GCF, which is 3. The GCF is then divided from both monomials, resulting in (2x²) and (1). The remaining terms are then divided, resulting in 2x. The answer to this equation is 2x.

Conclusion
This worksheet guide has provided students with the knowledge necessary to successfully tackle monomial multiplication and division word problems. Students should now be able to identify and solve monomial multiplication and division problems with ease.

Conclusion

The Multiplying And Dividing Monomials Worksheet is a great tool to help students understand and practice the process of multiplying and dividing monomials. With the worksheet, students can practice their skills and become more confident with the process. The worksheet also allows students to review their answers and make sure they understand the concept. This can help them be more successful in their math classes and in their future pursuits.