50 Midsegment Of A Triangle Worksheet | Chessmuseum Template Library with regard to Midsegment Theorem Worksheet Answer Key

Midsegment Theorem Worksheet Answer Key

by

Exploring the Basics of Midsegment Theorem Worksheet Answer Key

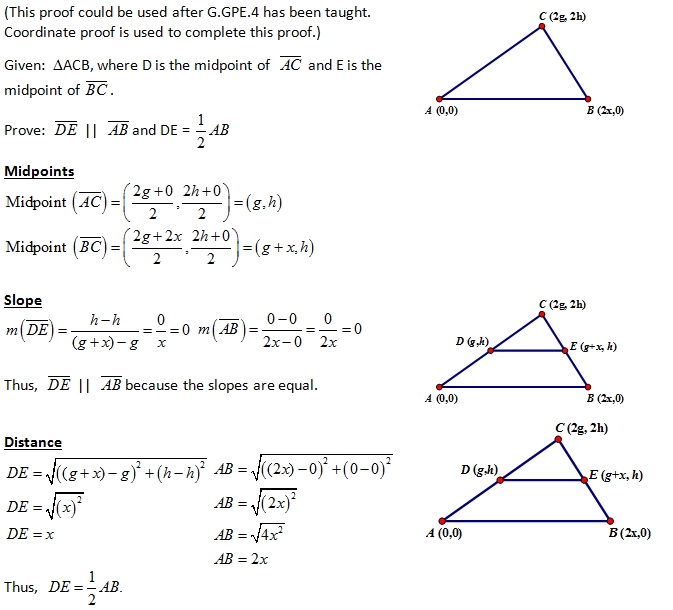
The Midsegment Theorem states that the line segment joining the midpoints of two sides of a triangle is parallel to the third side and is equal to half of its length. This theorem is useful for solving problems involving triangles.

50 Midsegment Of A Triangle Worksheet | Chessmuseum Template Library With Regard To Midsegment Theorem Worksheet Answer Key

To use the Midsegment Theorem, first find the midpoints of the two sides of the triangle. The midpoints are located by taking the average of the coordinates of the endpoints of the two sides. For example, if the coordinates of the endpoints of a line segment are (2, 3) and (4, 6), the midpoint would be (3, 4.5).

38 Midsegment Theorem Worksheet Answer Key - Worksheet Source 2021 In Midsegment Theorem Worksheet Answer Key

Once the midpoints are located, draw a line segment connecting them. This line segment is parallel to the third side of the triangle and is equal to one-half of its length. To find the length of the third side, multiply the length of the midsegment by two.

[toc]

The Midsegment Theorem is a useful tool in solving many problems involving triangles. It is important to remember that the line segment connecting the midpoints is parallel to the third side of the triangle, and is equal to one-half of its length.

50 Midsegment Of A Triangle Worksheet | Chessmuseum Template Library In Midsegment Theorem Worksheet Answer Key

Breaking Down How to Solve Midsegment Theorem Problems

Midsegment theorem problems are a type of geometry problem that can be solved using a specific set of principles. To solve a midsegment theorem problem, a clear understanding of the theorem and its underlying concepts is essential.

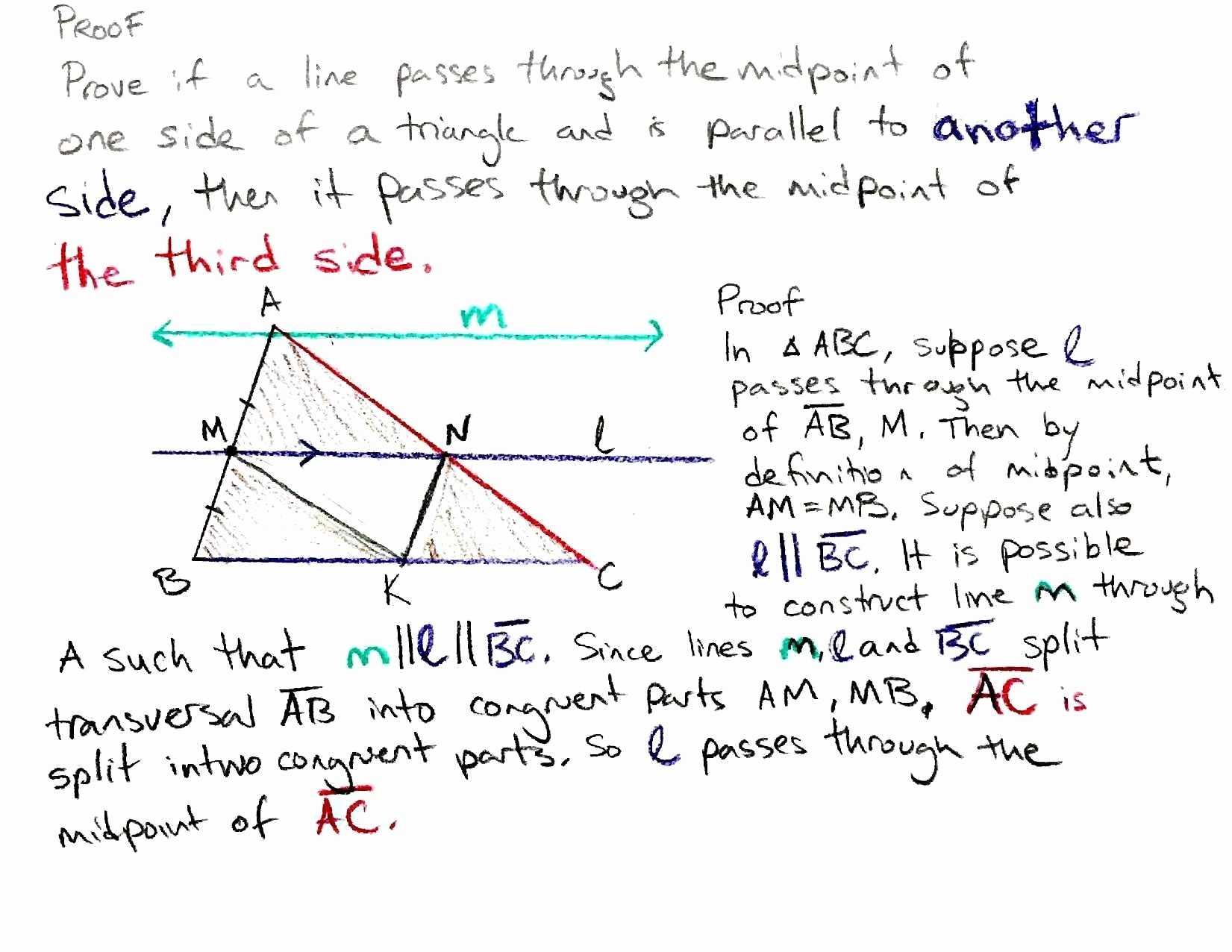
The first step in solving a midsegment theorem problem is to understand the theorem itself. The midsegment theorem states that a line segment connecting the midpoints of two sides of a triangle is equal in length to one-half of the third side. This means that in any triangle, the line segment connecting the midpoints of two of its sides will have the same length as half of the third side.

Unit 5 Relationships In Triangles Homework 1 Triangle Midsegments Answer Key - Islero Guide With Midsegment Theorem Worksheet Answer Key

The next step in solving a midsegment theorem problem is to draw a diagram of the triangle. This will help to visualize the triangle and its sides, and will be instrumental in solving the problem.

Once the diagram has been drawn, the next step is to label the sides and the midpoints. This will help to keep track of the various elements of the triangle.

50 Midsegment Of A Triangle Worksheet | Chessmuseum Template Library With Midsegment Theorem Worksheet Answer Key

The next step is to identify the midsegment of the triangle. This can be done by looking for the line segment that connects the midpoints of two of the sides. Once the midsegment has been identified, the lengths of the two sides that it connects can be determined.

The fourth step is to calculate the length of the midsegment. This can be done by adding the lengths of the two sides and dividing the sum by two. This will give the length of the midsegment.

The fifth step is to compare the length of the midsegment with the length of the third side. If the midsegment is equal in length to one-half of the third side, then the midsegment theorem has been proven. If the lengths are not equal, then the midsegment theorem has not been proven and further investigation is necessary.

By understanding the midsegment theorem and following these steps, anyone can solve midsegment theorem problems. With practice, solving midsegment theorem problems can become second nature.

Examining Different Types of Midsegment Theorem Worksheet Answer Key Formats

1. Textbook Format:
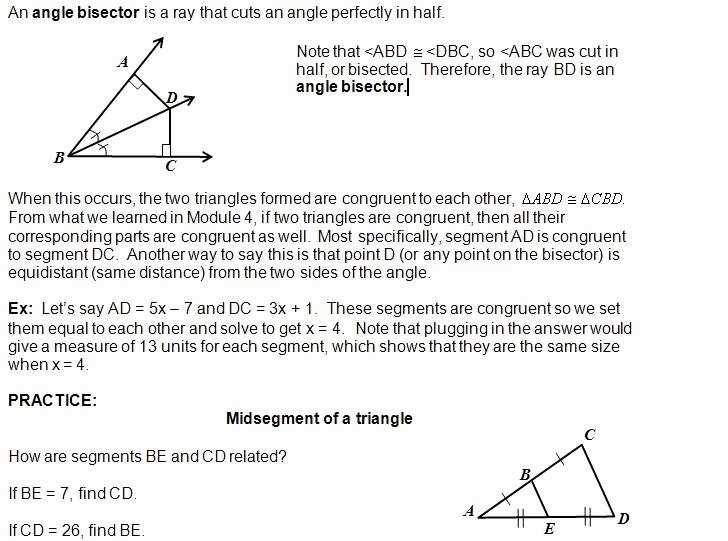
The Midsegment Theorem states that the midsegment of a triangle is parallel to the third side and it has a length equal to one-half the sum of the lengths of the two other sides. It is a useful tool for finding the length of the midsegment if the lengths of the two other sides are known.

2. Mathematical Format:
Let ABC be a triangle with midsegment DE. Then DE is parallel to BC and has length equal to half the sum of AB and AC. That is, DE = (1/2)(AB + AC).

3. Graphical Format:
A diagram of a triangle ABC, with midsegment DE shown as a parallel line between the points A and C, and labeled with the length of DE being equal to the sum of AB and AC divided by two.

4. Tabular Format:

Midsegment Theorem

Property | Statement
Midsegment is parallel to 3rd side | DE is parallel to BC
Midsegment length | DE = (1/2)(AB + AC)

Analyzing Midsegment Theorem Worksheet Answer Key Solutions and Strategies

The Midsegment Theorem states that the midsegment of a triangle is parallel to the third side of the triangle and is equal to one half of the sum of the lengths of the two sides it connects. This theorem is a useful tool when working with triangles and can help to make complex calculations easier.

In order to understand the Midsegment Theorem, it is important to understand the concept of a midsegment of a triangle. A midsegment is a line segment connecting the midpoints of two sides of a triangle. It is always parallel to the third side of the triangle and can be used to help calculate the lengths of the sides of the triangle.

The Midsegment Theorem can be used to solve a variety of problems, from finding the length of the missing side of a triangle to calculating the area of a triangle. When using the theorem, it is important to consider the lengths of the sides of the triangle, as well as the angles between them. It is also important to remember that the midsegment is equal to one half of the sum of the lengths of the two sides it connects.

In order to solve problems using the Midsegment Theorem, it is important to consider all of the available information. This includes the lengths of the sides of the triangle, as well as the angles between them. Once all of the information is gathered, it is possible to begin solving the problem. By applying the Midsegment Theorem, it is possible to solve a variety of problems that involve triangles.

The Midsegment Theorem is a useful tool when working with triangles. By understanding the theorem and how it can be used, it is possible to solve a variety of problems with ease. By applying the theorem, it is possible to solve problems involving the lengths of the sides of a triangle, as well as the angles between them. As long as the lengths and angles are known, the Midsegment Theorem can be used to make complex calculations much easier.

Conclusion

The Midsegment Theorem Worksheet Answer Key provides a comprehensive overview of the theorem and its application. It shows how to use the theorem to solve problems involving triangles, and provides examples to illustrate its use. By studying the worksheet and its answers, students can gain a better understanding of the theorem and its uses in geometry.

[addtoany]

5 photos of the "Midsegment Theorem Worksheet Answer Key"

50 Midsegment Of A Triangle Worksheet | Chessmuseum Template Library With Regard To Midsegment Theorem Worksheet Answer Key38 Midsegment Theorem Worksheet Answer Key – Worksheet Source 2021 In Midsegment Theorem Worksheet Answer Key50 Midsegment Of A Triangle Worksheet | Chessmuseum Template Library In Midsegment Theorem Worksheet Answer KeyUnit 5 Relationships In Triangles Homework 1 Triangle Midsegments Answer Key – Islero Guide With Midsegment Theorem Worksheet Answer Key50 Midsegment Of A Triangle Worksheet | Chessmuseum Template Library With Midsegment Theorem Worksheet Answer Key

Related posts of "Midsegment Theorem Worksheet Answer Key"

50 Lab Safety Worksheet Answers | Chessmuseum Template Library regarding Lab Safety Worksheet Answers

Lab Safety Worksheet Answers

Understanding the Necessity of Completing a Lab Safety Worksheet AnswerCompleting a lab safety worksheet is a critical step in ensuring the safety of those who work in a laboratory environment. In this setting, risks associated with hazardous materials and processes are often present, and it is essential to have a comprehensive understanding of the potential...

Heritage High: Teachers - Courses And Files inside Scientific Notation Worksheet Pdf

Scientific Notation Worksheet Pdf

How to Use Scientific Notation Worksheets to Improve Math SkillsScientific notation worksheets can be a great tool for improving math skills. By using these worksheets, students can learn how to write and interpret numbers in scientific notation. This can be beneficial for students of all ages and math levels, as it provides a more efficient...

14 Direct Variation Worksheets Printable / Worksheeto with regard to Direct Variation Word Problems Worksheet

Direct Variation Word Problems Worksheet

How to Use a Direct Variation Word Problems Worksheet to Enhance LearningA direct variation word problems worksheet can be a useful learning tool for students who are studying algebra. It allows them to practice solving algebraic problems that involve direct variation, which is a type of mathematical relationship between two variables. The worksheet can be...

30 Solving Trig Equations Worksheet | Education Template throughout Solve Trig Equations Worksheet

Solve Trig Equations Worksheet

Step-by-Step Guide to Solving Trig Equations with a WorksheetStep 1: Begin by familiarizing yourself with the terms used to describe trigonometric equations. Identify the type of equation, the angle measure, and any other relevant information. Step 2: Draw a diagram of the equation. A diagram can often help you to better understand the equation and...