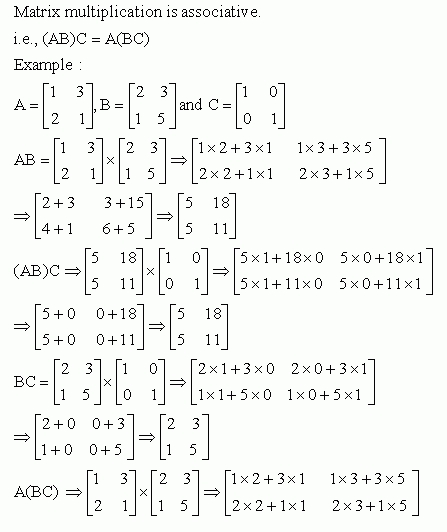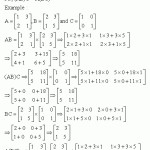How to Use Matrices Word Problems Worksheet to Improve Math Problem-Solving Skills

A matrices word problems worksheet is a valuable tool for improving math problem-solving skills. This worksheet provides students with practice working through matrix operations and equations, helping them to develop their understanding of the subject. By working through a variety of word problems, students can learn to identify the type of problem and then apply the appropriate operation to solve it.

The worksheet should begin with simple matrix operations, such as adding and subtracting matrices. As students become more comfortable with these operations, the worksheet can then progress to more complex operations, such as multiplying and dividing matrices. By working through these problems, students will develop the ability to identify the operations needed to solve the problem and to select the appropriate operation.

Once students are comfortable with basic matrix operations, they can move on to solving equations. Here, they will be required to identify the type of equation and then use the appropriate operation to solve it. This can provide a great opportunity for students to learn to recognize equations, as well as how to solve them.

[toc]

Finally, the worksheet should include a variety of word problems, which can help students to apply the matrix operations they have learned. These problems require students to think creatively and apply the operations to find solutions. By working through a variety of problems, students will become better problem solvers and will be better prepared to tackle complex math problems.

By working through a matrices word problems worksheet, students can develop their understanding of matrix operations, equations, and word problems. This worksheet can also provide them with the opportunity to practice their problem-solving skills and to become better prepared for more complex math problems.

Exploring the Different Types of Matrices Word Problems Worksheet

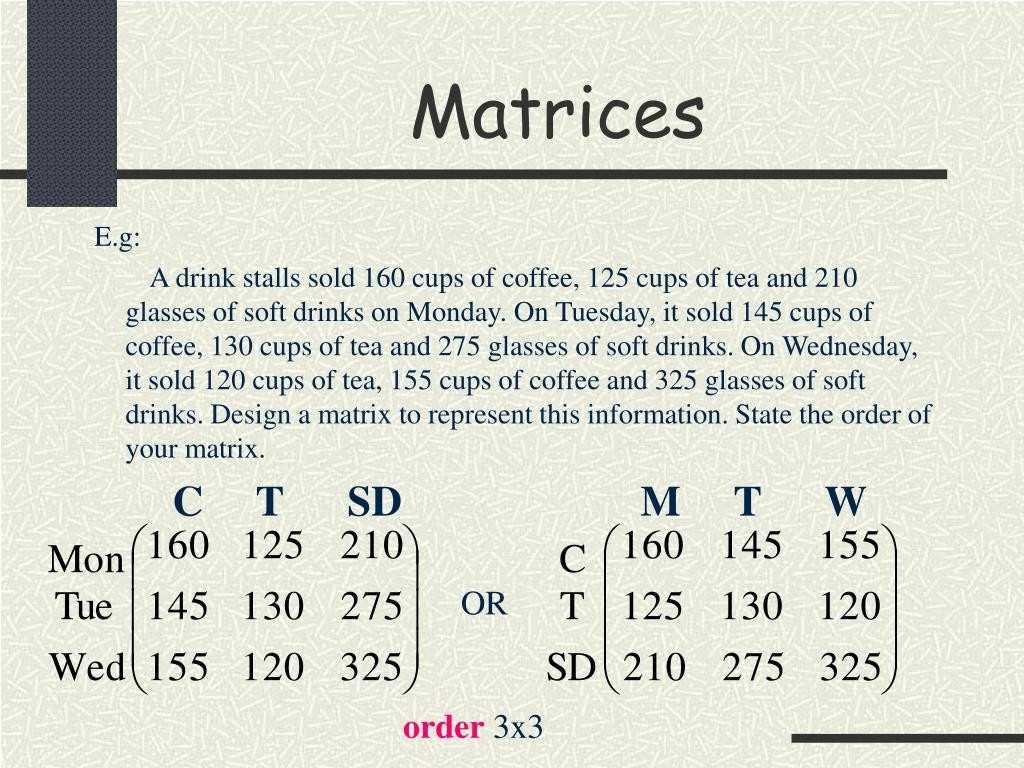
Matrices word problems are a powerful tool for solving a wide variety of mathematical problems. They can be used to solve linear equations, calculate probabilities, and even calculate the area of a triangle. In order to effectively use matrices, it’s important to understand the different types of matrices word problems and how to approach them.

The first type of matrices word problem is the linear equations problem. This type of problem involves setting up a matrix containing the equations, solving the equations, and then determining the solution. For example, in a linear equation, the matrix might look like this:

\begin{bmatrix}
1 & 2 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9
\end{bmatrix}

This matrix can be used to solve for the unknown variables in the equation. For example, if we are asked to solve for x, we can multiply the first row of the matrix with x, as shown below:

1*x + 2*y + 3*z = 0

This equation can then be solved using the standard methods of linear algebra.

The second type of matrices word problem is the probability problem. This type of problem involves using the matrix to calculate the probability of a certain outcome. For example, if there are three different outcomes, each with a certain probability, the matrix will look like this:

\begin{bmatrix}
0.25 & 0.50 & 0.25
\end{bmatrix}

The probability of each outcome can be determined by multiplying the row vector by the column vector of the matrix. For example, if we are asked to calculate the probability of outcome B, we can multiply the first row vector by the second column vector, as shown below:

0.25*0.50 = 0.125

This result indicates that the probability of outcome B is 0.125.

The third type of matrices word problem is the area of a triangle problem. This type of problem involves using the matrix to calculate the area of a triangle given the lengths of its three sides. For example, if we are given the lengths of three sides of a triangle, the matrix will look like this:

\begin{bmatrix}
3 & 4 & 5
\end{bmatrix}

The area of the triangle can be determined by multiplying the row vector by the column vector of the matrix. For example, if we are asked to calculate the area of the triangle, we can multiply the first row vector by the second column vector, as shown below:

3*4*5 = 60

This result indicates that the area of the triangle is 60.

These are just a few examples of the different types of matrices word problems. By understanding the different types of problems, it’s possible to effectively use matrices to solve a wide variety of mathematical problems.

Strategies for Working Through Difficult Matrices Word Problems Worksheet

1. Break Down the Problem: Before attempting to solve a difficult matrix word problem, it is important to take a step back and break down the problem into smaller, more manageable parts. Analyze each part of the problem and identify the key pieces of information that need to be addressed. This can include variables, equations, matrices, and more. Once the key elements of the problem have been identified, it is easier to determine how to approach the problem.

2. Utilize Strategies: Once the problem has been broken down, it is possible to use a variety of strategies to solve the problem. In particular, matrices can be used to solve linear equations, which can help reduce the complexity of the problem. Additionally, the use of substitution, elimination, and other techniques can help simplify the problem even further.

3. Identify All Possible Solutions: When working through a difficult matrix word problem, it is important to consider all possible solutions. Many times, there may be multiple solutions to a single problem, and it is important to identify and consider each one. This can help ensure that the most efficient and accurate solution is found.

4. Check Your Work: After solving the problem, it is important to check your work to ensure that the solution is correct. This can be done by testing various values against the problem and ensuring that they result in the correct solution. Additionally, it is important to double-check the solution to make sure that it is consistent with the initial problem.

By utilizing these strategies, it is possible to work through difficult matrix word problems in an efficient and effective manner. Taking the time to break down the problem and consider all possible solutions can help reduce the complexity of the problem and ensure that the most accurate solution is found. Additionally, checking your work is essential to making sure that the correct solution is found.

Tips for Teaching Students to Solve Matrices Word Problems Worksheet Effectively

1. Encourage students to read the problem carefully and then identify the relevant information. Point out that the goal is to translate the problem into a matrix equation, so it is important to make sure they understand the problem before they attempt to solve it.

2. Ask the students to identify the variables in the problem, such as the number of items, the cost of each item, and any discounts or other factors that affect the total cost.

3. Model how to write the matrix equation by plugging in the values for each variable. Show how to solve for the missing variable.

4. Explain that the matrix equation is useful because it allows students to solve for multiple variables at the same time.

5. Encourage students to practice solving matrix equations in order to become comfortable with the process.

6. Ask students to check their work by substituting the solutions they found into the original problem to ensure that the answer is correct.

7. Remind students that they should always double check their work and ask questions if they are unsure of the answer.

Conclusion

The Matrices Word Problems Worksheet is a great resource for students to use when learning about matrices and their applications in real life. It provides a variety of problems that help to reinforce the concepts of matrices and can also be used to practice problem solving skills. By understanding and applying the techniques of matrices, students will be able to better solve real-world problems involving matrices.

[addtoany]