Exploring the Benefits of Using a Graphing Quadratic Functions Worksheet for Improved Math Understanding

A graphing quadratic functions worksheet is an essential tool for students to gain a better understanding of the quadratic equation and its application in mathematics. Quadratic equations are used to model a variety of real-world phenomena, including projectile motion, the growth of populations, electrical circuits, and even oscillations. By understanding the fundamental principles of quadratic equations, students can gain an appreciation for the power of mathematics to explain the natural world.

The graphing quadratic functions worksheet is an effective tool for improving math understanding. This worksheet presents the quadratic equation in a visual format, allowing students to easily identify the pattern of the graph. By plotting the points on the graph, students can quickly identify the corresponding values of the equation variables. This type of visual representation helps to reinforce the concept of the quadratic equation, which can often be difficult for students to grasp.

The graphing quadratic functions worksheet encourages students to think critically about the graph. As they observe the graph, students can ask themselves questions such as what the equation is telling them, why it looks the way it does, and how the equation is related to real-world phenomena. This type of inquiry-based learning can help students develop problem-solving skills and gain a deeper understanding of the quadratic equation.

The graphing quadratic functions worksheet also helps students develop a better understanding of the relationship between the equation variables. By plotting the points on the graph, students can quickly identify how the values of the variables affect the equation’s outcome. This type of analysis can help students to gain an appreciation for the power of mathematics to explain the natural world.

In conclusion, the graphing quadratic functions worksheet is an effective tool for improving math understanding. By providing students with a visual representation of the equation and allowing them to explore the relationship between the variables, this worksheet encourages critical thinking and problem-solving. In addition, it can help to reinforce the concept of the quadratic equation, which can often be difficult for students to grasp.

How to Interpret Graphing Quadratic Functions Worksheet Answers for Maximum Results

Interpreting graphing quadratic functions worksheets can be a challenging task. To maximize the results of your interpretation, it is important to first understand the basics of quadratic functions. Quadratic functions are equations that have a single variable squared, such as x2 + 4x + 3. The graph of a quadratic function is a parabola, which is a U-shaped curve.

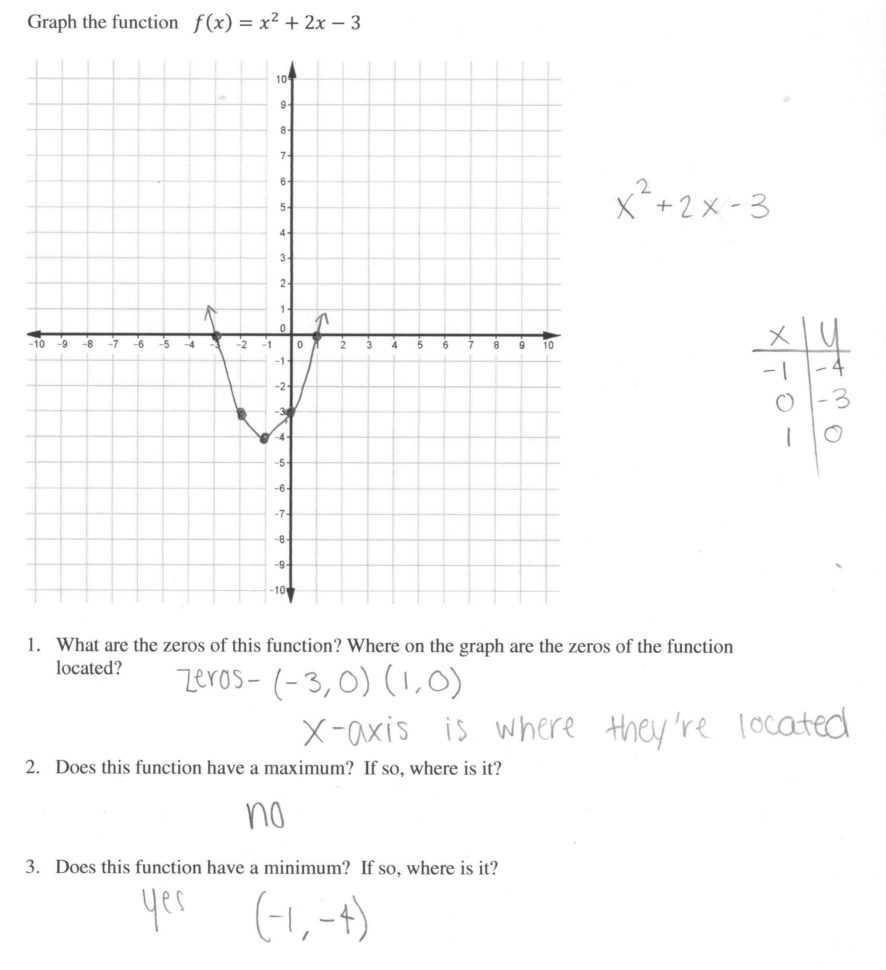
When interpreting the graphing quadratic functions worksheet, you should look for the following information: the equation of the parabola, the x-intercepts, the y-intercept, the vertex, the domain, the range, and the zeros. The equation of the parabola will tell you the shape of the graph. The x-intercepts are the points at which the graph crosses the x-axis, and the y-intercept is the point at which the graph crosses the y-axis. The vertex is the point at which the parabola turns, and the domain and range are the possible values of the x and y variables. Finally, the zeros are the points at which the graph intersects the x-axis.

Once you have identified this information, you can use it to interpret the worksheet answers. For instance, if the worksheet answer states that the graph has a y-intercept of (3, 0), you can interpret this to mean that the graph crosses the y-axis at the point (3, 0). Similarly, if the answer states that the graph has two zeros at (2, 0) and (-4, 0), you can interpret this to mean that the graph intersects the x-axis at these two points.

By understanding the basics of quadratic functions and interpreting the answers on a graphing quadratic functions worksheet, you can maximize your results and gain a better understanding of the graph.

Applying the Tips and Tricks of Graphing Quadratic Functions to Improve Accuracy

The graphing of quadratic functions is a common task in algebra and calculus, and accuracy is essential for successful problem solving. Fortunately, several tips and tricks can be used to ensure that graphs of quadratic functions are as accurate as possible.

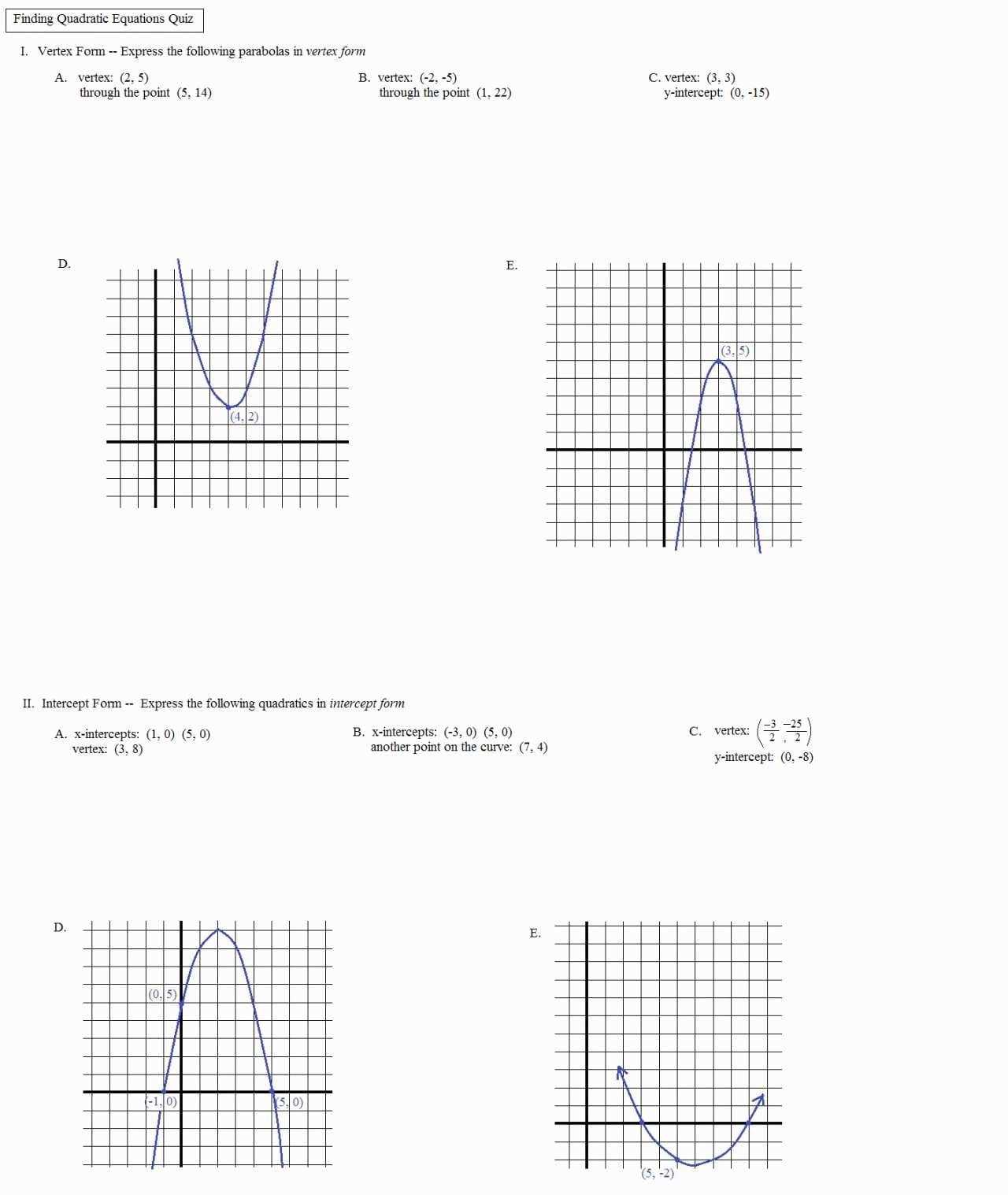
First, it is important to remember that the graph of a quadratic function is a parabola. This means that the graph should be symmetrical around the line called the axis of symmetry. To find the axis of symmetry, it is necessary to find the vertex of the parabola, which is the highest or lowest point on the graph. This is found by solving the equation for x when it is written in the form ax2 + bx + c = 0.

Once the vertex has been found, the axis of symmetry can be calculated by taking the average of the x-coordinates for the two solutions of the equation. The equation for the axis of symmetry is x = -b/(2a). Once the axis of symmetry has been found, the graph should be symmetrical around this line.

The next step is to plot points along the parabola. A good way to do this is to pick points that are evenly spaced on either side of the axis of symmetry. This ensures that the parabola will be symmetrical and accurate.

Finally, it is important to remember that the graph of a quadratic function must pass through the origin, which is the point where the x and y axes intersect. This should be checked to ensure accuracy.

By following these tips and tricks, the graphing of quadratic functions can be made much more accurate. With practice and patience, the graph of any quadratic function can be plotted with precision.

Unlocking the Potential of Graphing Quadratic Functions Worksheets to Solve Complex Math Problems

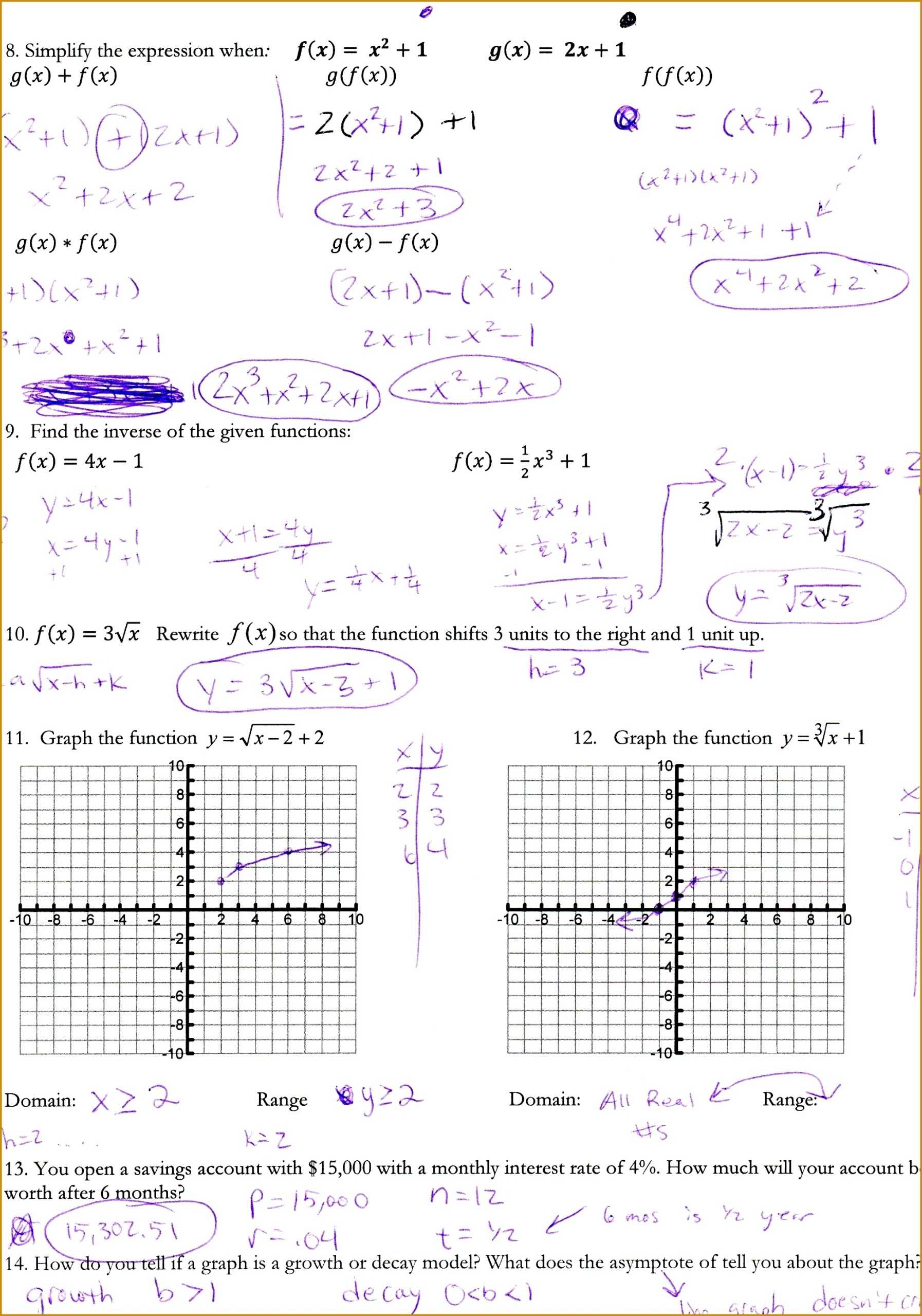
Graphing quadratic functions is one of the most powerful tools in solving complex math problems. By plotting points on a graph, students can easily identify the shape of the curve, the direction of its slope, and the location of its roots. This knowledge can be used to solve a variety of mathematical problems, from finding the area of a parabola to determining the coordinates of an intersection point. In order to unlock the full potential of graphing quadratic functions, students need to be familiar with the equations and how to interpret them.

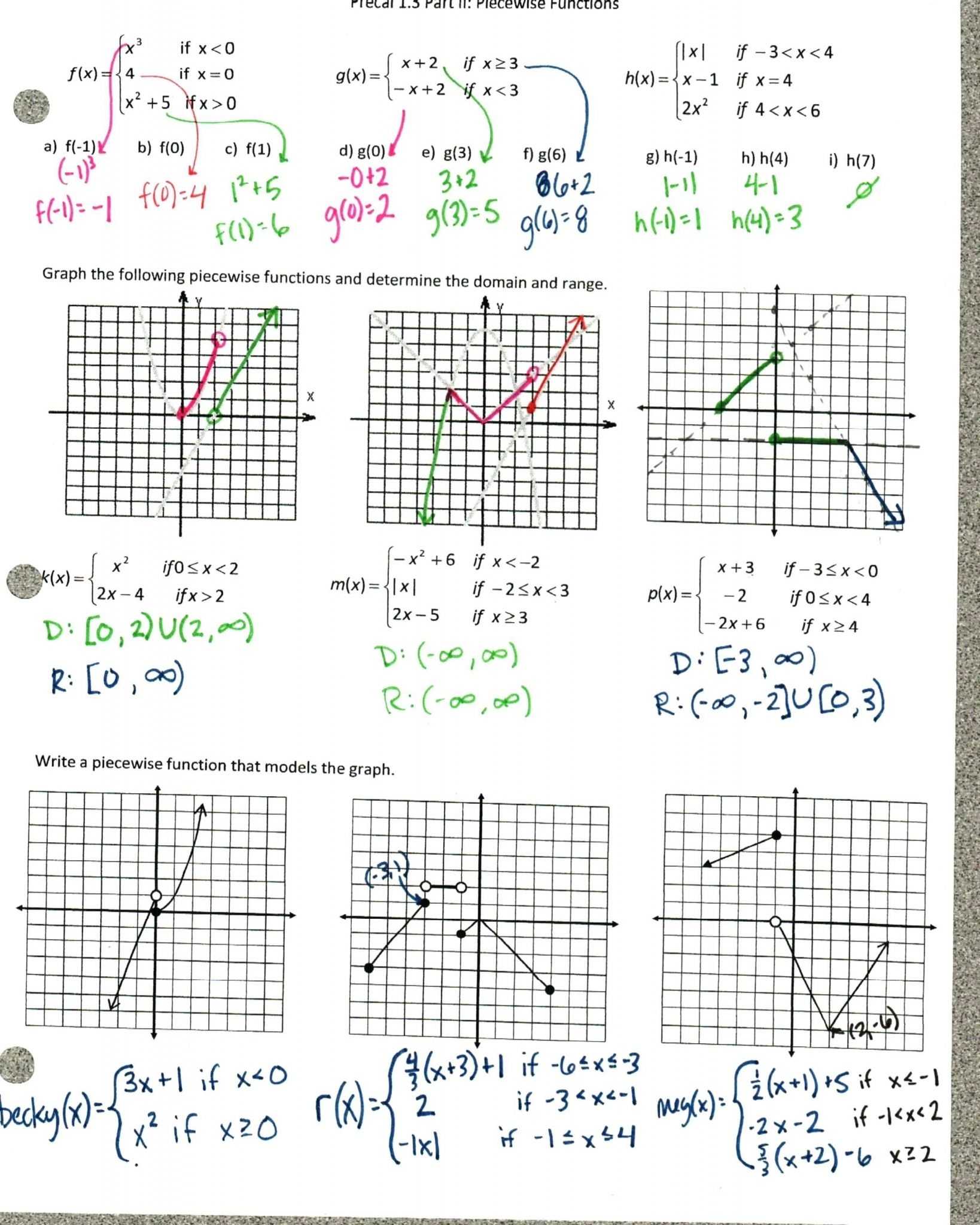
The best way to gain familiarity with graphing quadratic functions is through the use of worksheets. Worksheets provide students with a structured environment to practice graphing quadratic equations. They provide step-by-step instructions for understanding the equations and how to graph them. By following the instructions, students can learn how to identify the different types of curves and how to draw the graph accurately.

Worksheets also help students practice how to interpret the graph. For instance, students need to be able to identify the roots, the maximum or minimum points, and the turning points. By following the instructions on the worksheet, students can practice these skills, allowing them to solve complex math problems more quickly and accurately.

Worksheets also provide students with an opportunity to practice the mathematical operations required to solve quadratic equations. By identifying the equations, students can practice how to solve for the roots, the maximum or minimum points, and the turning points. This practice helps students gain confidence in their mathematical problem solving ability.

Finally, worksheets provide students with a visual representation of the graph. By studying the graph, students can learn how to identify the different types of curves and the direction of its slope. This knowledge can be used to help students solve complex math problems more easily.

By using graphing quadratic functions worksheets, students can unlock the potential of graphing quadratic functions and use them to solve complex math problems. With practice, students will gain confidence in their mathematical problem solving ability.

Conclusion

In conclusion, the Graphing Quadratic Functions Worksheet Answers provides a comprehensive overview of the graphing of a quadratic function and its corresponding solutions. It offers a comprehensive step-by-step guide to solve quadratic equations, graph the corresponding quadratic equation, and interpret the results. The worksheet also provides helpful tips and tricks to help users better understand the concepts of quadratic equations and graphing. With this resource, students will be able to gain a better understanding of the principles of graphing quadratic functions, and be better prepared to solve and graph quadratic equations.