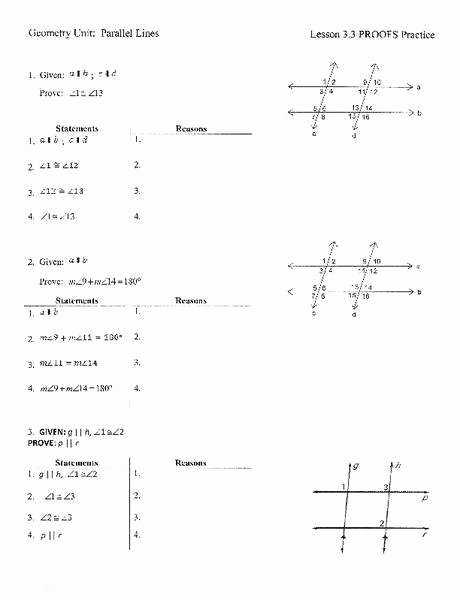
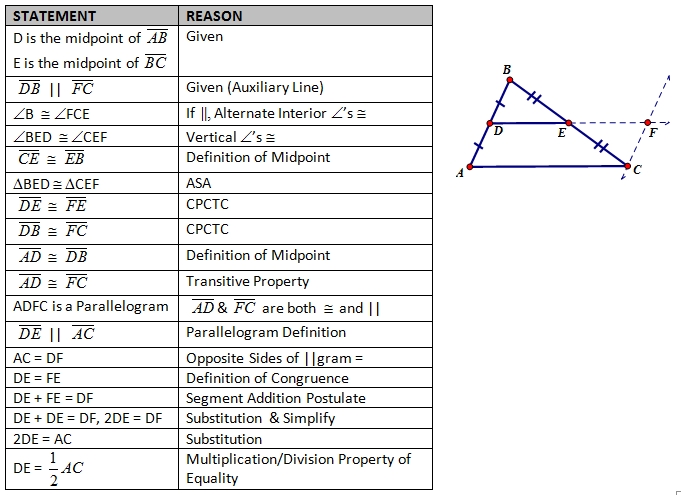
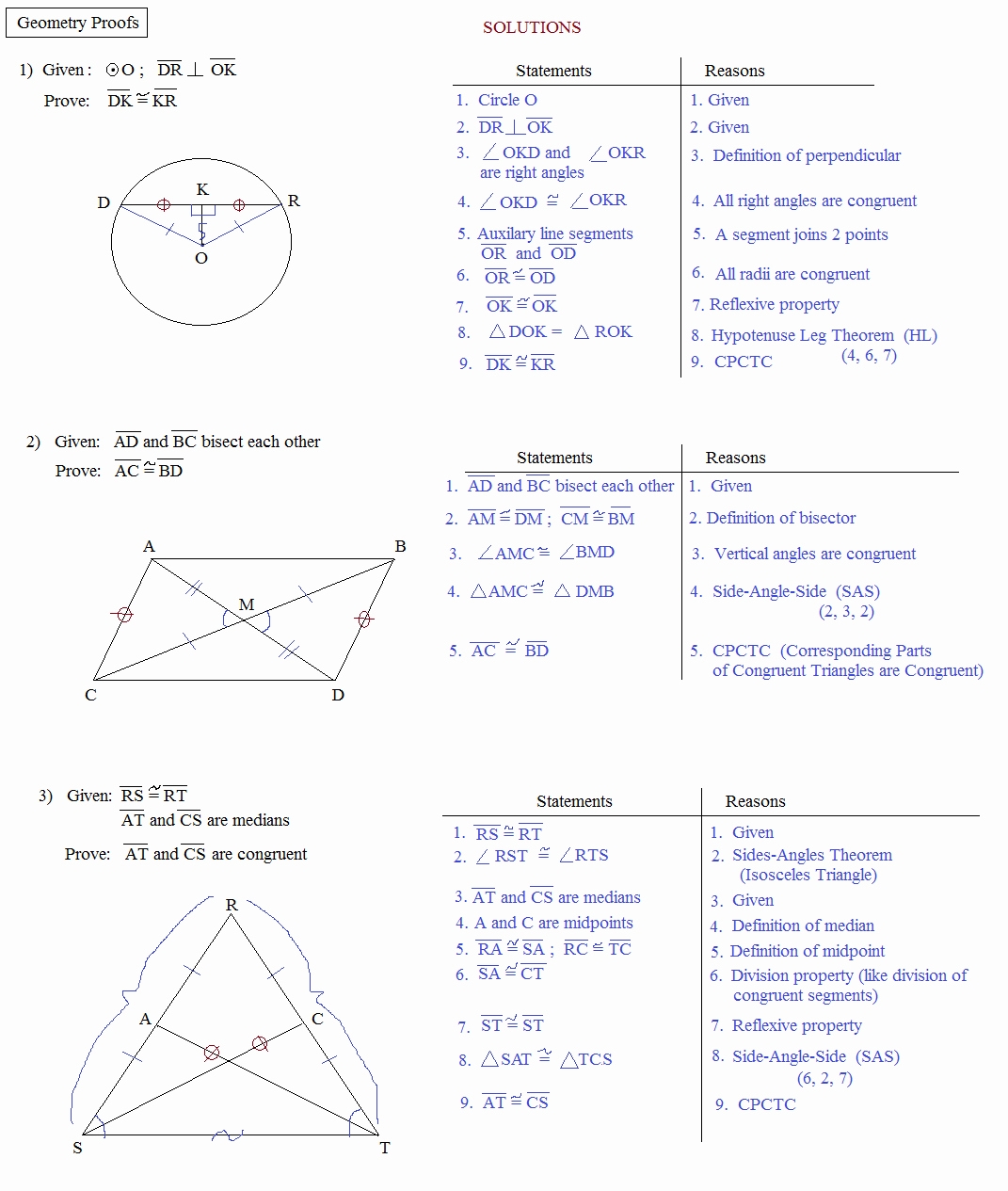
Proving Geometric Theorems: A Step-by-Step Guide Using a Geometric Proofs Worksheet

Geometric theorems are statements that are used to describe different geometric shapes and structures. Proving these theorems can be challenging, but rewarding. With a geometric proofs worksheet, anyone can prove these theorems step-by-step.

The first step in proving a geometric theorem is to read the statement and understand its meaning. Once the statement is understood, the next step is to sketch the statement to form a diagram. This diagram will be your foundation for the proof.

After the diagram is in place, the next step is to label the various parts of the diagram. This will help when you begin to write the proof. When labeling, you should use the given information from the statement as well as any known facts that may be pertinent to the proof.

Now that you have labeled the diagram, you are ready to begin writing the proof. Begin by writing the statement at the top of the proof. The statement should include the theorem you are trying to prove, as well as any known facts or assumptions you are using to prove the theorem.

Below the statement, begin writing the steps of your proof. With each step, use the labeled parts of the diagram to explain what is happening. Explain how the elements of the proof connect to each other and why they are necessary for the proof.

Once you have written all of the steps, the next step is to review the proof for accuracy. Make sure that each step is logical and that the conclusion of the proof is the same as the theorem you are trying to prove.

Finally, when you have reviewed the proof and determined that it is correct, you are ready to submit it. Using a geometric proofs worksheet is a great way to prove geometric theorems. With a few simple steps, anyone can prove these theorems and gain a better understanding of geometry.

Exploring the Benefits of Using a Geometric Proofs Worksheet with Answers

A Geometric Proofs Worksheet with Answers can be a helpful tool for teaching geometry to students. Geometry is a subject that requires students to be able to reason logically and think abstractly. As such, it can be difficult for students to understand the concepts being presented. Using a Geometric Proofs Worksheet with Answers can help students better understand the material by providing them with a step-by-step approach to each problem.

The Geometric Proofs Worksheet with Answers will typically include a set of questions and answers for each problem. These questions and answers will cover the following topics: identifying the type of problem being solved, setting up the appropriate equations, determining the correct solution, and constructing a proof. With each question, students will be provided with an explanation of the problem and the solution. This will help them understand the concepts behind the problem and how to approach it correctly.

The Geometric Proofs Worksheet with Answers will also provide students with a way to practice their skills. As students work through the problems, they can check their answers against the provided answers and make sure they have the correct solution. This can give students a sense of confidence when they are working through more difficult problems.

Using a Geometric Proofs Worksheet with Answers can also be beneficial to teachers. By providing students with a set of questions and answers, teachers can be sure that their students are getting the right answers. This can help to ensure that students are learning the material effectively and that they are able to apply their knowledge to real life situations.

Overall, using a Geometric Proofs Worksheet with Answers can be a great way to help students learn geometry. The provided questions and answers provide students with an organized approach to each problem and can help them better understand the concepts behind the problem. In addition, the practice questions and answers can help students build confidence and ensure that they are getting the correct solution. Using a Geometric Proofs Worksheet with Answers can be a great way to help students understand and apply geometry.

Tips for Successfully Completing Geometric Proofs Worksheets with Answers

1. Read the Entire Problem Carefully: Before you start attempting to solve a geometric proof, it is important to read the entire problem carefully in order to understand what it is asking and what you need to prove. You should also check to see if there are any diagrams or figures included that could help you understand the problem better.

2. Identify the Given Information: To successfully complete a geometric proof, you will need to understand the given information in the problem. This includes the given statements, diagrams, and any other pertinent information. You should highlight or make note of the given information so that you can refer to it throughout the proof.

3. Plan Your Strategy: Once you have read and identified the given information, you should plan your strategy. This will help you stay organized and save you time. You should decide how you will approach the problem and create a logical order for the steps that you will take.

4. Use the Given Information to Make Conclusions: As you work through the problem, you should use the given information to make conclusions. Draw out diagrams or figures that help illustrate your conclusions, as this can make the proof easier to follow and understand.

5. Write Out Your Solution: Once you have worked through the problem and made your conclusions, you should write out your solution in a clear, organized manner. Explain each step of your proof and make sure that your proof follows the logical order that you planned out earlier.

6. Check Your Work: Finally, once you have written out your solution, it is important to check your work. Look over the proof again to make sure that it is logically sound and that all of the necessary steps have been included. Additionally, make sure that your proof meets all of the requirements outlined in the problem.

A Comprehensive Guide to Geometric Proofs Worksheets with Answers for High School Mathematics

Introduction
Geometric proofs are an essential part of high school mathematics. They allow students to explore the concepts of geometry by expressing the relationships between geometric shapes and figures. Geometric proofs are an important part of understanding the structure and properties of two-dimensional and three-dimensional shapes, and they are a key component of geometry classes.

The purpose of this guide is to provide students with an introduction to geometric proofs and provide them with a set of worksheets and accompanying answers that they can use to practice and refine their understanding of these skills. The worksheets cover a variety of topics, from basic proofs to more advanced ones, so that students can gain a comprehensive understanding of geometric proof techniques.

What Is a Geometric Proof?
A geometric proof is a logical argument that uses properties of geometric figures and shapes to demonstrate a statement. In a geometric proof, the statement is either accepted as true or false and then the proof is used to show why the statement must be true. The proof must use deductive reasoning and logical steps to lead to the conclusion.

Types of Geometric Proofs
There are several types of geometric proofs that students should be aware of. These include direct proofs, indirect proofs, proof by contradiction, and proof by contrapositive. Each type of proof relies on specific rules and properties of geometry to build a logical argument.

Direct Proofs
Direct proofs are the simplest form of geometric proof. In a direct proof, the statement is assumed to be true, and then the proof follows a series of steps that logically lead to the conclusion. This type of proof is often used when proving statements that involve the properties of geometric figures, such as the Pythagorean Theorem.

Indirect Proofs
Indirect proofs are similar to direct proofs, except that instead of assuming the statement to be true, the proof starts by assuming the statement to be false. This type of proof is often used to prove theorems that involve multiple figures, such as the Angle-Angle-Side Theorem.

Proof by Contradiction
Proof by contradiction is a more advanced form of geometric proof. This type of proof starts by assuming that the statement is false, and then follows a series of steps that lead to a contradiction. The contradiction then shows that the statement must be true. This type of proof is often used to show that a set of statements is impossible to achieve.

Proof by Contrapositive
Proof by contrapositive is a type of proof that involves proving the opposite of a statement. To do this, the proof starts by assuming the opposite statement to be true, and then follows a series of steps that logically lead to the conclusion that the original statement must be true. This type of proof is often used to prove theorems that involve multiple figures, such as the Triangle Inequality Theorem.

Worksheets and Answers
This guide includes a variety of worksheets and accompanying answers that can be used to help students practice and refine their understanding of geometric proof techniques. The worksheets cover a range of topics, from basic proofs to more advanced ones, so that students can gain an understanding of the different types of proofs and how to apply them.

Conclusion
Geometric proofs are an important part of high school mathematics, and they can be used to explore the structure and properties of two-dimensional and three-dimensional shapes. This

Conclusion

The Geometric Proofs Worksheet With Answers is an excellent tool for helping students understand and practice the basics of geometric proofs. With this worksheet, students can learn how to identify and draw valid geometric proofs, as well as how to construct and use valid logical arguments. This worksheet is a great way to introduce students to the concepts of geometric proofs and help them develop critical thinking skills.