How to Use a Visual Model to Teach Students About Dividing Fractions

A visual model is an effective tool for teaching students about dividing fractions. This model helps to provide a concrete representation of the mathematical concept, allowing students to more easily grasp the concept. To use a visual model to teach students about dividing fractions, the following steps should be followed.

First, explain to the students that division of fractions involves dividing the numerator by the denominator. To better illustrate this, draw a fraction bar on the board and explain that the top number is the numerator and the bottom number is the denominator.

Second, provide students with a visual representation of division of fractions. For example, draw a pie chart on the board and label the pie slices with fractions. Explain that each pie slice represents a fraction, and that division of fractions involves dividing the numerator of one fraction by the denominator of another fraction.

Third, ask the students to work on a problem together. For example, give them a problem such as “What is 3/4 divided by 2/3?” Show them how to divide the numerator of one fraction (3) by the denominator of the other fraction (2), then multiply the result (3/2) by the second fraction (2/3) to get the final answer (9/6).

Finally, provide the students with additional practice problems to reinforce the concept. Ask them to solve the problems on their own, then check their answers together.

By following these steps, a teacher can effectively use a visual model to teach students about dividing fractions. This model provides a concrete illustration of the concept and allows students to more easily understand the process of dividing fractions.

Understanding the Math Behind Dividing Fractions with a Worksheet

Understanding the mathematics behind dividing fractions can be a difficult task for many students. In order to help provide clarity and a better understanding of the concept, a worksheet can be a helpful resource.

When dividing fractions, the numerators and denominators of each fraction must be manipulated in order to arrive at the solution. The first step is to invert the second fraction. This means that the numerator and denominator switch places. For example, if the fraction is two-thirds (2/3), it becomes three-halves (3/2).

Once this is accomplished, the fractions are then multiplied. This means that the numerator of the first fraction is multiplied by the numerator of the second fraction and the denominator of the first fraction is multiplied by the denominator of the second fraction. This results in the solution.

A worksheet can provide step-by-step instructions to practice the mathematics behind dividing fractions. Each problem on the worksheet will provide an example of a fraction that needs to be divided. The student must then follow the instructions to invert the second fraction and then to multiply the two fractions together in order to arrive at the solution.

By completing a worksheet on dividing fractions, a student can gain a better understanding of the mathematics behind the concept. The worksheet can also provide a great way to practice the math and to ensure that the student is confidently able to divide fractions.

Exploring Strategies and Problems to Master Dividing Fractions through a Worksheet

Dividing fractions can be a difficult mathematical concept for many students to master. A worksheet can be an effective tool to help students practice and develop their skills in this area.

When designing a worksheet to help students master dividing fractions, it is important to include problems of varying levels of difficulty. This allows students to practice and build their confidence gradually. Begin by posing basic problems that involve simple fractions, such as 1/2 divided by 1/4. As students gain confidence and accuracy, increase the complexity of the fraction equations, introducing more difficult fractions and more complicated computations.

In addition to providing practice problems, it is also beneficial to include a section on strategies to help students solve problems involving dividing fractions. It can be helpful to explain common methods such as the Inverse Property of Multiplication or using a common denominator to convert fractions into equivalent fractions. It can also be useful to provide specific tips and tricks, such as converting fractions to decimals before dividing.

Including a few multiple choice questions on the worksheet can also be beneficial. This allows students to practice and test their knowledge without having to solve the problem themselves.

Finally, it is important to include a section on problem-solving. This can help students understand the process of solving fractions problems, rather than simply memorizing the answers. For example, a problem-solving section could ask students to explain the steps taken to solve a dividing fraction equation, or to identify the mistakes made in a given problem.

Overall, a worksheet can be a useful tool for helping students master dividing fractions. By including problems of varying difficulty and providing strategies, tips, tricks and problem-solving practice, students can gain the knowledge and skills needed to solve fractions problems with confidence.

Conclusion

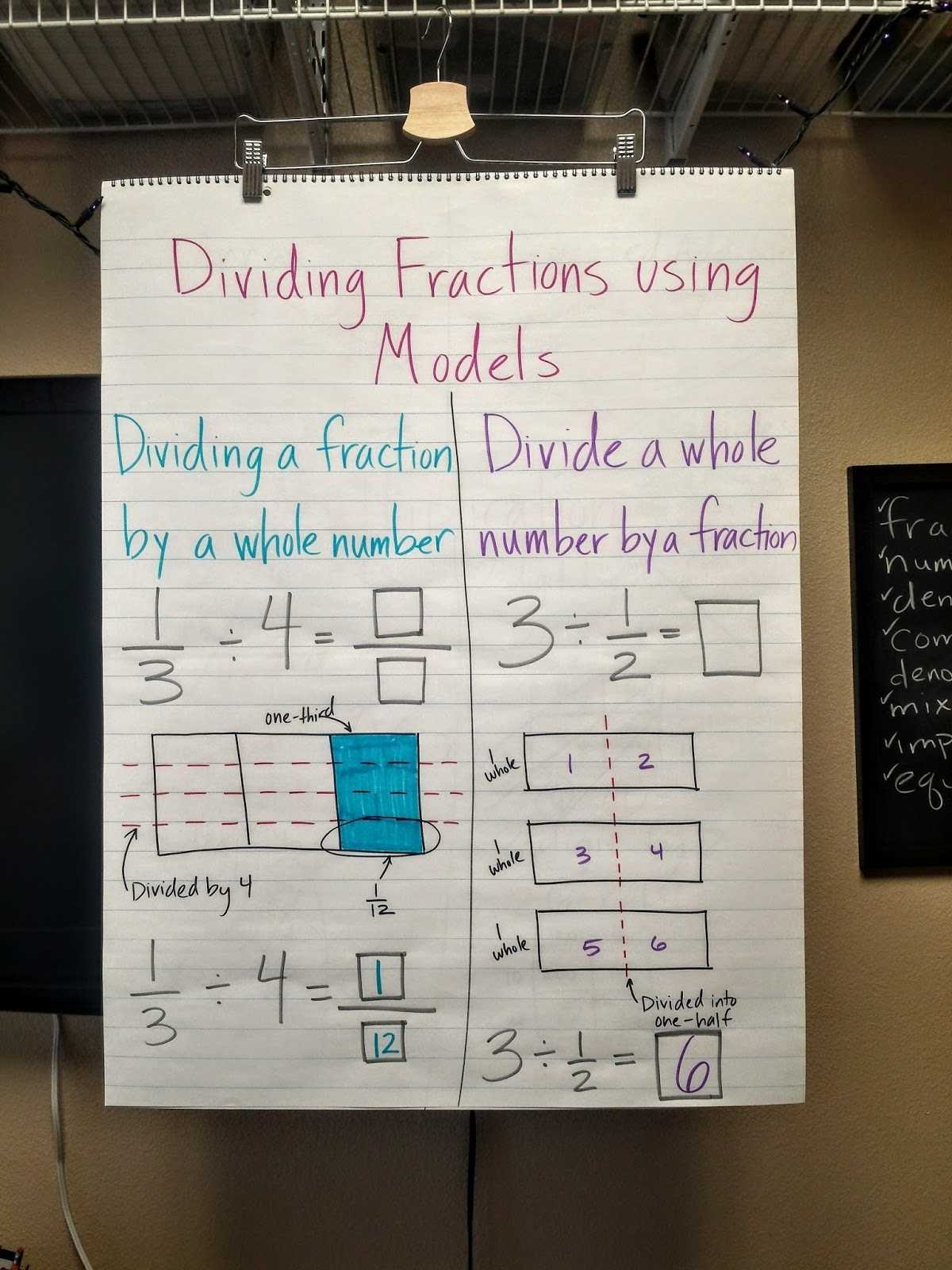
The Dividing Fractions Using Models Worksheet provides an engaging and effective way for students to practice their fraction division skills. It is a great resource for teachers to use as it helps students understand the concept of fraction division through visual representation and encourages them to think critically. Furthermore, it can be used to assess student knowledge and help identify areas of improvement. Overall, the worksheet is an invaluable tool for teachers to use in their fraction instruction.