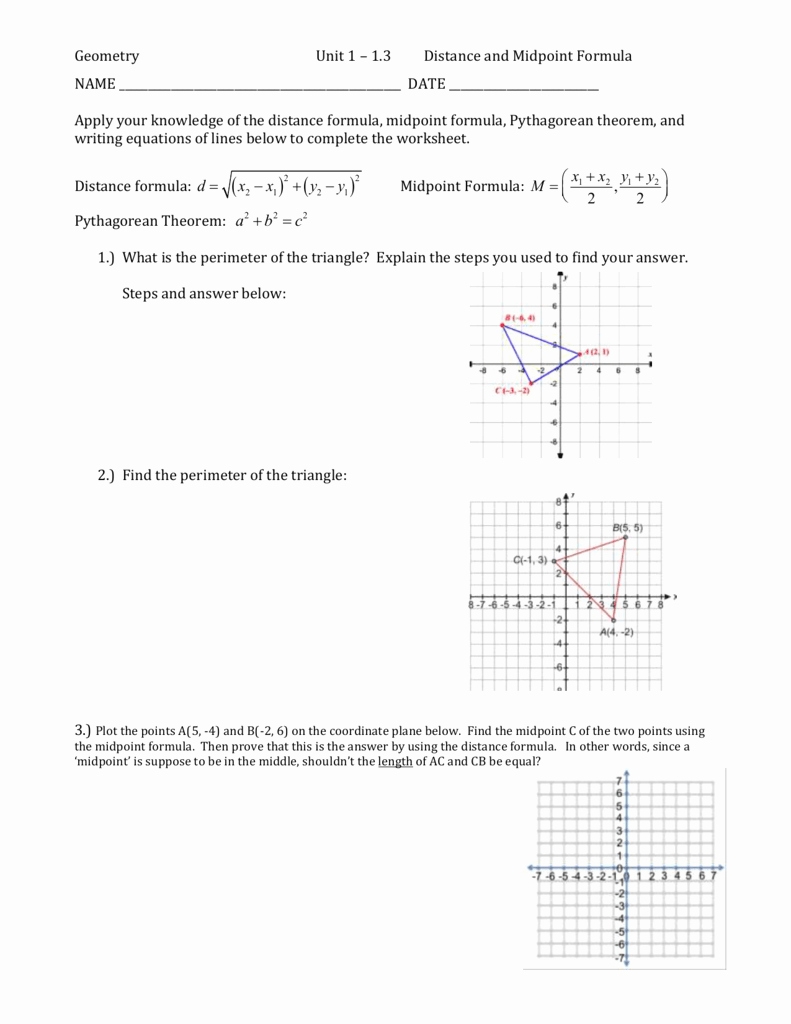
How to Use a Distance and Midpoint Worksheet to Calculate the Distance Between Two Points.

Calculating the distance between two points can be a difficult task for those who are unfamiliar with mathematics. Fortunately, a distance and midpoint worksheet can be used to simplify the process. This worksheet consists of a grid with two points, labeled A and B, in which the user inputs the x and y coordinates of each point.

To begin, the user must input the coordinates of both Point A and Point B into the worksheet. The coordinates of each point are typically listed in order of the x-axis and y-axis. For example, if Point A has an x-coordinate of 2 and a y-coordinate of 4, it would be written as (2, 4). After both coordinates have been inputted, the user must calculate the midpoint between Point A and Point B. This is done by taking the average of the two points’ x-coordinates and y-coordinates, respectively, and writing the answer in the midpoint section of the worksheet.

Finally, to calculate the distance between Point A and Point B, the user must calculate the difference between the x-coordinates and the y-coordinates of the two points. The user then takes the sum of these differences and calculates the square root of the result. This result is the distance between Point A and Point B.

By using a distance and midpoint worksheet, users can easily learn how to calculate the distance between two points. This worksheet can be used to solve a variety of mathematical problems, making it a valuable tool for anyone studying mathematics.

Exploring the Relationship Between Distance and Midpoint: A Look at Common Graphs and Functions.

When exploring the relationship between distance and midpoint, it is important to understand the various common graphs and functions associated with this concept. The most commonly used graphs are the linear graph and the parabolic graph.

The linear graph is a straight line, drawn on a two-dimensional graph, that represents a relationship between two variables. In the case of distance and midpoint, the linear graph would represent the relationship between the distance between two points and the midpoint of those points. The equation for this relationship is y = (x1 + x2)/2, where x1 and x2 represent the two points and y represents the midpoint.

The parabolic graph is a curved line, drawn on a two-dimensional graph, that represents a relationship between three variables. In the case of distance and midpoint, the parabolic graph would represent the relationship between the distance between three points and the midpoint of those points. The equation for this relationship is y = (x1 + x2 + x3)/3, where x1, x2, and x3 represent the three points and y represents the midpoint.

When analyzing the relationship between distance and midpoint, it is important to understand the various common functions associated with this concept. The two most commonly used functions are the distance function and the midpoint function.

The distance function is a mathematical formula that calculates the distance between two points, given their coordinates. The equation for this function is d = √((x2 – x1)^2 + (y2 – y1)^2), where (x1, y1) and (x2, y2) represent the coordinates of the two points and d represents the distance between them.

The midpoint function is a mathematical formula that calculates the midpoint of two points, given their coordinates. The equation for this function is (x, y) = ((x1 + x2)/2, (y1 + y2)/2), where (x1, y1) and (x2, y2) represent the coordinates of the two points and (x, y) represent the coordinates of the midpoint.

By understanding the various common graphs and functions associated with the relationship between distance and midpoint, it is possible to gain a better understanding of this concept. By analyzing these graphs and functions, it is possible to gain insight into how distance and midpoint are related and how they can be used to calculate distances and midpoints between two or three points.

Understanding the Concept of Distance and Midpoint Through Simple Examples.

Distance is a term used to describe the length between two points. It is often measured in miles, kilometers, or any other unit of length. In mathematics, the distance between two points can be calculated using the Pythagorean Theorem. The formula for the distance between two points (x1,y1) and (x2,y2) is:

d = √(x2−x1)2 + (y2−y1)2

The midpoint is a point that lies halfway between two other points. It can be calculated by taking the average of the coordinates of the two points. The formula for finding the midpoint between two points (x1,y1) and (x2,y2) is:

Mx = (x1 + x2) / 2

My = (y1 + y2) / 2

For example, if we have two points located at (3, 4) and (8, 10), we can use the above formulas to find the distance and midpoint between the two points.

The distance between the two points is calculated as follows:

d = √(8−3)2 + (10−4)2

d = √(52)

d = 7.2

The midpoint between the two points is calculated as follows:

Mx = (3 + 8) / 2

Mx = 11 / 2

Mx = 5.5

My = (4 + 10) / 2

My = 14 / 2

My = 7

Therefore, the midpoint between the two points (3, 4) and (8, 10) is (5.5, 7).

Creating a Distance and Midpoint Worksheet to Practice Math Skills.

This worksheet is designed to help students practice their math skills by calculating distances and midpoints between two given points. The worksheet contains a series of problems involving two points in a coordinate plane and asks students to calculate the distance and midpoint between them.

The worksheet begins by providing students with an explanation of how to calculate the distance and midpoint between two points. It then provides a few practice problems that involve calculating the distance and midpoint between two points in the coordinate plane. After the practice problems, the worksheet contains a series of problems that involve calculating the distance and midpoint between two points in the coordinate plane.

To complete the worksheet, students must calculate the distance and midpoint between two given points. To do this, they must first calculate the distance between the two points by subtracting the x- and y-coordinates of the first point from the x- and y-coordinates of the second point. Then, they must calculate the midpoint by taking the average of the two x- and y-coordinates.

This worksheet can be used to help students develop their math skills by reinforcing the concepts of distance and midpoint calculations. It also provides an opportunity to practice their understanding of the coordinate plane and how to calculate distances and midpoints between two points.

Conclusion

In conclusion, Distance and Midpoint Worksheets are an excellent way to practice and reinforce the concepts of finding the distances and midpoints of lines and shapes. Distance and Midpoint Worksheets are easy to use and provide a great visual aid for students to use to understand the material. They are a great tool to use in the classroom to help students better understand the concepts of distance and midpoints.