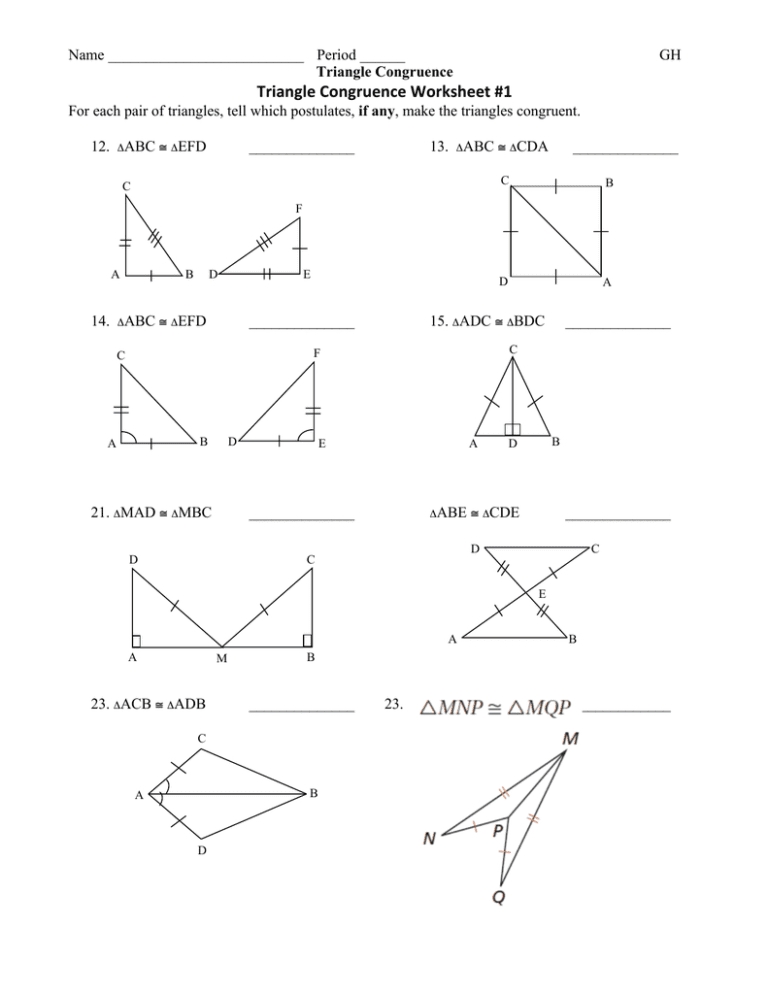
Exploring Congruent Triangles: A Comprehensive Worksheet With Answers

Congruent triangles are an important topic in geometry, as they are the foundation for many other geometric concepts. This worksheet will provide a comprehensive exploration of congruent triangles and their properties. The questions and answers provided will help students understand the concept of congruent triangles and how to use them in geometry.

Question 1: What are congruent triangles?

Answer: Congruent triangles are two triangles that have the same size and shape. In order for two triangles to be congruent, all three sides and all three angles must be equal.

[toc]

Question 2: What are the three ways to prove that two triangles are congruent?

Answer: There are three ways to prove that two triangles are congruent: Side-Side-Side (SSS), Side-Angle-Side (SAS), and Angle-Side-Angle (ASA). In the SSS method, all three sides of each triangle must be equal in length. In the SAS method, two sides and the included angle of each triangle must be equal. In the ASA method, two angles and the included side of each triangle must be equal.

Question 3: What is the Angle-Angle-Side (AAS) theorem?

Answer: The Angle-Angle-Side (AAS) theorem states that if two angles and a side of one triangle are congruent to two angles and a side of a second triangle, then the two triangles are congruent. This theorem is useful in proving that two triangles are congruent without having to calculate all three angles or all three sides.

Question 4: How can congruent triangles be used in construction?

Answer: Congruent triangles can be used in construction for laying out walls, foundations, roof lines, and other structures. By ensuring that two triangles are congruent, builders can be sure that the structure they are constructing is of the correct size, shape, and angle. This is especially helpful when building structures that must fit together perfectly, such as a bridge or a house.

Question 5: What is the Triangle Inequality Theorem?

Answer: The Triangle Inequality Theorem states that the sum of any two sides of a triangle must be greater than the third side. This theorem is useful in determining whether a given set of measurements can form a triangle and in proving that two triangles are not congruent.

Unraveling the Mysteries of Congruent Triangles: A Step-by-Step Worksheet With Answers

Introduction

The concept of congruent triangles can be a challenging one for students to understand. Congruent triangles are two triangles that have the same size and shape. They can be found in both two-dimensional and three-dimensional figures. This worksheet will provide a step-by-step approach to unraveling the mysteries of congruent triangles.

Step 1: Identify the Triangles

The first step in understanding congruent triangles is to identify the triangles in the figure. To do this, look for triangles that have the same number of sides and angles. In addition, look for triangles that have the same length of each side and the same angle measurements.

Step 2: Identify the Similarities

Once the triangles have been identified, look for any similarities between them. This can include the same side lengths, the same angle measurements, or the same line of symmetry. Once all similarities have been noted, it becomes easier to determine if the triangles are congruent.

Step 3: Use the Definition of Congruence

The next step is to look at the definition of congruence. According to the definition, two triangles are congruent if they have the same size and shape. This means that they must have the same side lengths and the same angle measurements.

Step 4: Use the SSS Method

The SSS method can be used to determine if two triangles are congruent. This method stands for side-side-side. To use this method, look at the side lengths of the two triangles. If the side lengths of both triangles are equal, then the two triangles are congruent.

Step 5: Use the SAS Method

The SAS method can also be used to determine if two triangles are congruent. This method stands for side-angle-side. To use this method, look at the side lengths of both triangles and the angle measurements. If the side lengths and angle measurements of both triangles are equal, then the two triangles are congruent.

Conclusion

By following these steps, students can easily unravel the mysteries of congruent triangles. With practice, they can quickly identify congruent triangles in any figure. As students become more comfortable with the concept of congruent triangles, they can move on to more complex figures that involve three-dimensional objects.

Applying the Rules of Congruent Triangles: A Comprehensive Worksheet With Answers

This worksheet is designed to provide students with a comprehensive understanding of the rules of congruent triangles. Congruent triangles are two triangles which have all sides and angles of equal measure. This worksheet will provide students with detailed explanations of the three main rules of congruent triangles. It will also provide examples to illustrate each concept, as well as practice problems for students to complete.

The first rule of congruent triangles is known as the Side-Side-Side (SSS) rule. This rule states that if all three sides of two triangles are equal in length, then the two triangles are congruent. To illustrate this concept, consider the following example.

Triangle ABC and triangle DEF have all three sides equal in length. This means that triangle ABC and triangle DEF are congruent, as they both share the same three sides.

The second rule of congruent triangles is known as the Side-Angle-Side (SAS) rule. This rule states that if two sides and the included angle of two triangles are equal, then the two triangles are congruent. To illustrate this concept, consider the following example.

Triangle GHI and triangle JKL have two sides and the included angle equal in measure. This means that triangle GHI and triangle JKL are congruent, as they both share the same two sides and the included angle.

The third and final rule of congruent triangles is known as the Angle-Side-Angle (ASA) rule. This rule states that if two angles and the included side of two triangles are equal, then the two triangles are congruent. To illustrate this concept, consider the following example.

Triangle MNO and triangle PQR have two angles and the included side equal in measure. This means that triangle MNO and triangle PQR are congruent, as they both share the same two angles and the included side.

To test your understanding of the rules of congruent triangles, try completing the following practice problems.

1. Are triangle ABC and triangle DEF congruent?

Yes, triangle ABC and triangle DEF are congruent. This is because all three sides of the triangles are equal in length, which satisfies the Side-Side-Side (SSS) rule.

2. Are triangle GHI and triangle JKL congruent?

Yes, triangle GHI and triangle JKL are congruent. This is because the two triangles share two sides and the included angle, which satisfies the Side-Angle-Side (SAS) rule.

3. Are triangle MNO and triangle PQR congruent?

Yes, triangle MNO and triangle PQR are congruent. This is because the two triangles share two angles and the included side, which satisfies the Angle-Side-Angle (ASA) rule.

Conclusion

The congruent triangles worksheet with answers provided a great way for students to practice their knowledge of congruent triangles. It provided them with an opportunity to apply their understanding of congruent triangle rules and to think about how to apply those rules to solve the problems. The questions on the worksheet also allowed students to practice identifying congruent triangles and to compare various shapes to determine their similarity. By working through the worksheet, students were able to gain a better understanding of the principles of congruent triangles, which will help them to better solve problems involving them in the future.

[addtoany]