Exploring the Unit Circle: A Comprehensive Guide to Understanding the Unit Circle Worksheet with Answers

Introduction
The unit circle is an important mathematical concept that is used in a wide range of applications, from physics and engineering to calculus and trigonometry. The unit circle is a circle with a radius of one unit and is centered at the origin. It is used to represent angles in the Cartesian plane and is an essential tool for solving many geometric problems. This guide will provide a comprehensive overview of the unit circle, including its definition, properties, and applications.

Definition of the Unit Circle
The unit circle is a circle with a radius of one unit and is centered at the origin. It is defined by the equation x2 + y2 = 1, which states that the distance from the origin to any point on the circle is always equal to one unit. The unit circle is used to graph angles in the Cartesian plane, as each point on the circle corresponds to an angle in the range 0° to 360°.

Properties of the Unit Circle
The unit circle has several important properties that make it a useful tool for graphing angles. Firstly, the radius of the circle is always one unit, no matter what angle it is representing. Secondly, the angle formed by the radius and the x-axis is always 90°. Thirdly, the circumference of the unit circle is always two pi units. Finally, the unit circle can be divided into four quadrants, each of which has its own distinct properties.

Applications of the Unit Circle
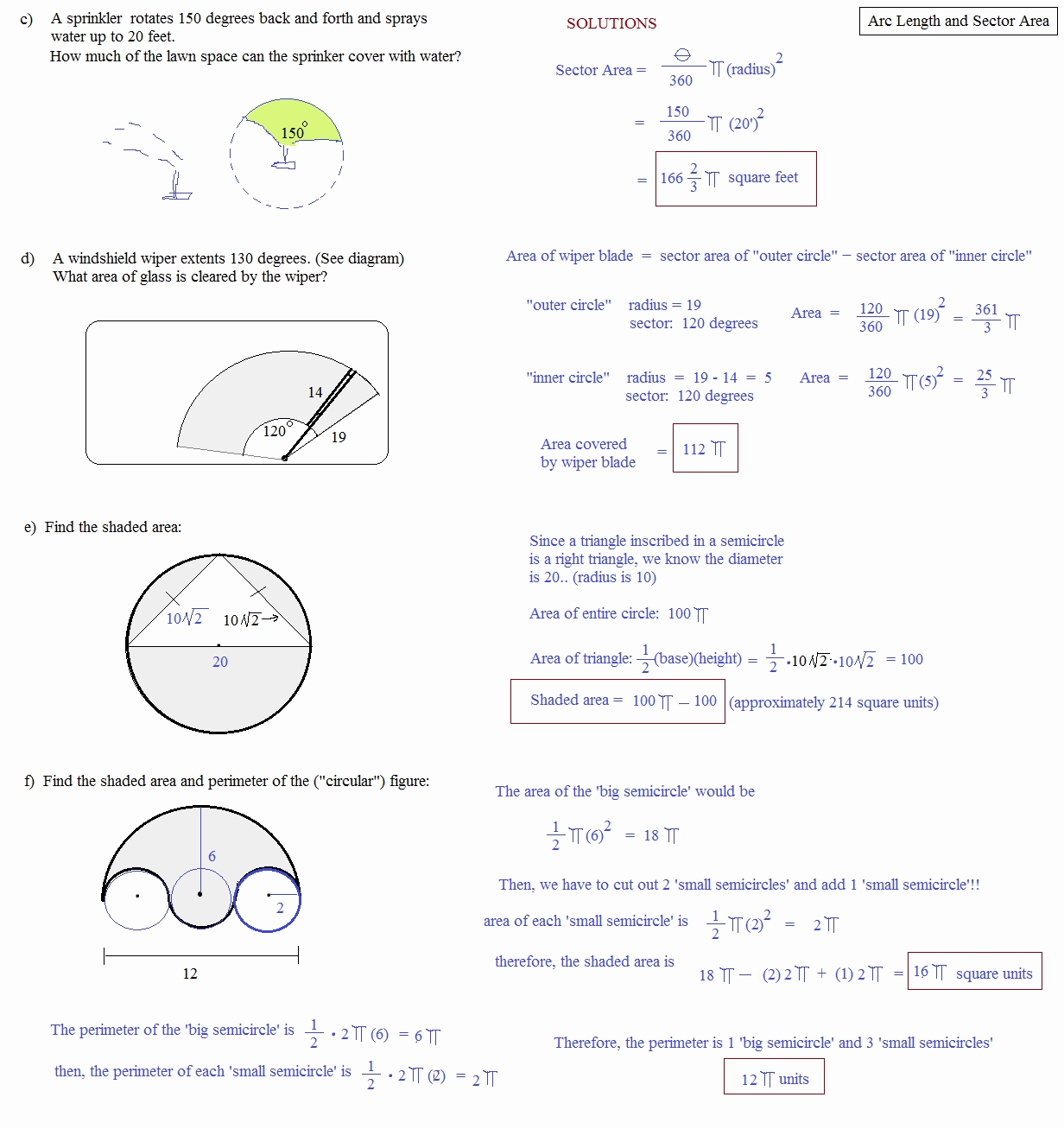
The unit circle is a versatile tool that has a range of applications. It is commonly used in trigonometry and calculus to calculate the sine and cosine of angles, as well as to solve equations involving angles. In physics, the unit circle is used to calculate the magnitude and direction of forces and other vectors. In engineering, it can be used to calculate the motion of objects in two dimensions. Finally, it can be used in geometry to calculate the area of a circle or to solve problems involving angles and lengths.

Conclusion
The unit circle is an important concept in mathematics that has a range of applications. This guide has provided a comprehensive overview of the unit circle, including its definition, properties, and applications. With this knowledge, you will be able to use the unit circle to solve a variety of mathematical problems.

How to Use the Unit Circle Worksheet with Answers to Enhance Your Math Skills

The unit circle worksheet with answers is a powerful tool for students to enhance their math skills. By working through the worksheet, students can develop a better understanding of the unit circle and its applications in mathematics. With this worksheet, students can learn to identify the radian measure of angles, calculate the coordinates of points on the unit circle, and understand the relationship between the unit circle and trigonometric functions.

To get the most out of the worksheet, it is important for students to focus on the questions and answers. As they work through the worksheet, they should pay close attention to the explanations provided. This will help them to understand the concepts and apply them to their math lessons. Additionally, students should take time to practice their skills by solving the problems on their own.

Once students have completed the worksheet, they should review their answers. This will help them to identify any mistakes they may have made and correct them. Students can also use the worksheet to practice their skills in order to prepare for exams.

The unit circle worksheet with answers is a great way for students to develop their math skills. By working through the worksheet, students can gain a better understanding of the unit circle and its use in mathematics. In addition, students can practice their skills and prepare for exams. With the worksheet, students can become more confident in their math abilities.

Strategies for Mastering the Unit Circle Worksheet with Answers

1. Memorize the Degrees: The first step to mastering the unit circle is to learn and memorize the different degrees and the associated radian measurements. Memorizing the degrees will help you quickly identify the reference angle, which is used to calculate the trigonometric functions of the angle in the unit circle.

2. Memorize the Quadrants: The unit circle is divided into four quadrants, each containing different degrees and associated radian measurements. Memorizing the degree and radian values of each quadrant will help you quickly identify the associated trigonometric functions.

3. Understand the Relationships: Understanding the relationships between the different trigonometric functions and the angles in the unit circle will help you quickly identify the correct trigonometric functions for a given angle. For example, understanding that sine is positive in the first and second quadrants and negative in the third and fourth quadrants will help you quickly identify the correct sine value for a given angle.

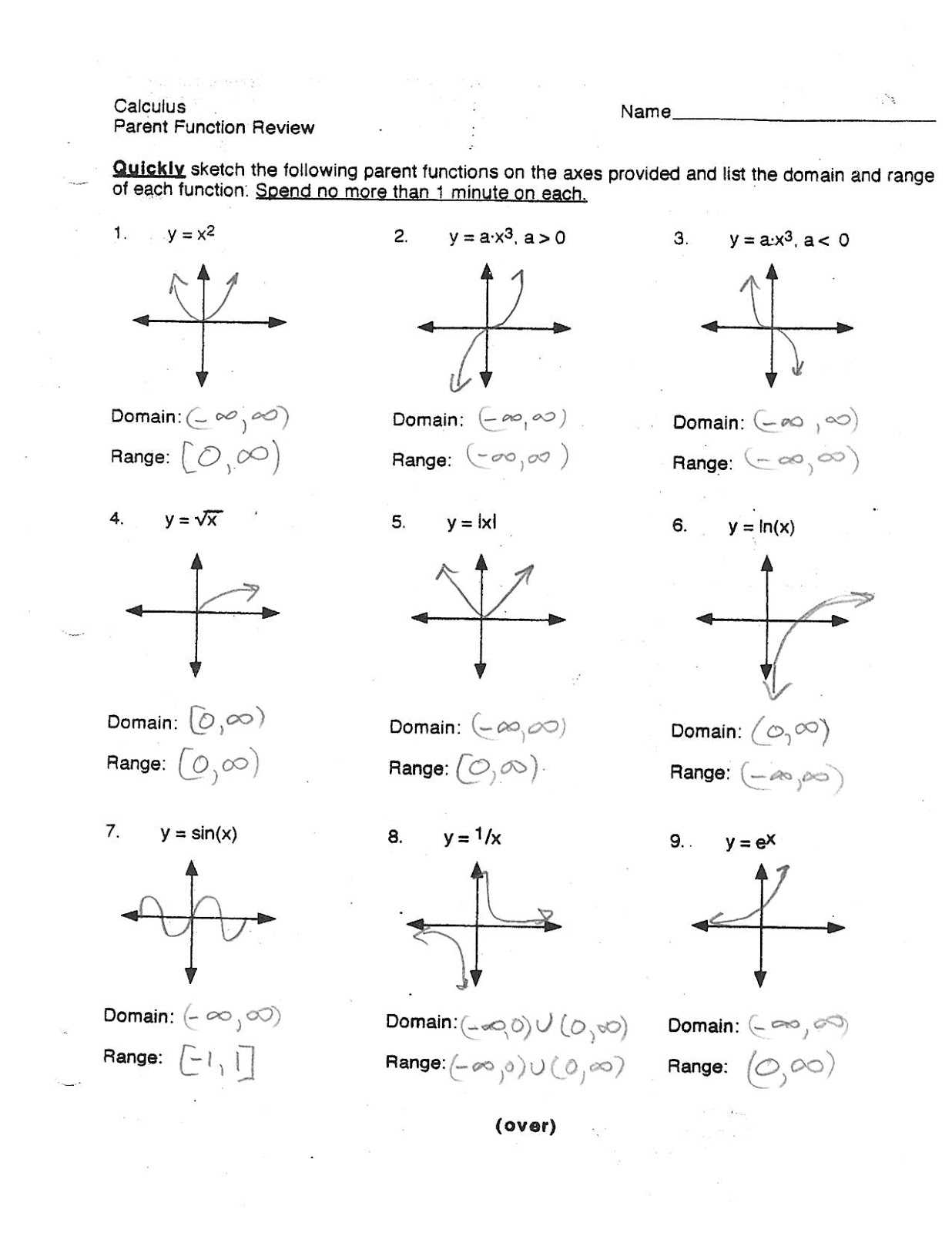
4. Draw the Circle: Draw out the circle and fill in the angles and associated radian measurements. Drawing out the circle will help you visualize the angles and trigonometric functions, which can make it easier to solve problems related to the unit circle.

5. Practice: The best way to master the unit circle is to practice. Work through as many problems as you can, paying special attention to the degree and radian measurements associated with each angle. With enough practice, you will eventually become familiar enough with the unit circle to be able to solve problems quickly and accurately.

Unpacking the Trigonometric Identities with the Unit Circle Worksheet with Answers

Trigonometric identities are equations that express the relationships between the trigonometric functions. Understanding these identities can be greatly aided by using the unit circle, which is a circle with a radius of one unit. This worksheet will help you to unpack these identities by using the unit circle.

The first trigonometric identity to unpack is the identity for the sine of an angle. This identity states that the sine of an angle is equal to the y-coordinate of the point on the unit circle associated with the angle. To begin, draw a unit circle on a blank piece of paper, and label the angles in the angles in the circle. To find the y-coordinate of the point associated with an angle, draw a line from the origin to the point of the angle. The y-coordinate of the point is the length of this line.

The next identity to unpack is the identity for the cosine of an angle. This identity states that the cosine of an angle is equal to the x-coordinate of the point on the unit circle associated with the angle. To find the x-coordinate of the point associated with an angle, draw a line from the origin to the point of the angle. The x-coordinate of the point is the length of this line.

The next identity to unpack is the identity for the tangent of an angle. This identity states that the tangent of an angle is equal to the ratio of the y-coordinate of the point on the unit circle associated with the angle to the x-coordinate of the point associated with the angle. To find the tangent of an angle, draw a line from the origin to the point of the angle. Calculate the ratio of the y-coordinate of the point to the x-coordinate of the point. This is the tangent of the angle.

The final identity to unpack is the identity for the cotangent of an angle. This identity states that the cotangent of an angle is equal to the ratio of the x-coordinate of the point on the unit circle associated with the angle to the y-coordinate of the point associated with the angle. To find the cotangent of an angle, draw a line from the origin to the point of the angle. Calculate the ratio of the x-coordinate of the point to the y-coordinate of the point. This is the cotangent of the angle.

By using the unit circle to unpack the trigonometric identities, you can gain a better understanding of these equations and their relationships with each other.

Conclusion

This Unit Circle worksheet with answers provides a great opportunity for students to practice and review their knowledge of the unit circle. It includes a variety of questions and diagrams that can help students develop a better understanding of the concepts behind the unit circle. With the help of this worksheet, students can gain a deeper understanding of the relationships between angles, radians, and the unit circle. It can also help students to better understand the relationship between trigonometric functions and the unit circle.