Unpacking the Basics: Exploring Trigonometric Ratios Worksheet Answers

Trigonometric Ratios are essential mathematical tools used to determine the length and angle of a triangle. These ratios are used in a variety of disciplines including engineering, physics, and astronomy. They are also an important part of basic geometry and algebraic equations. In this worksheet, we will explore the fundamentals of trigonometric ratios and how they are used to calculate the length and angles of a triangle.

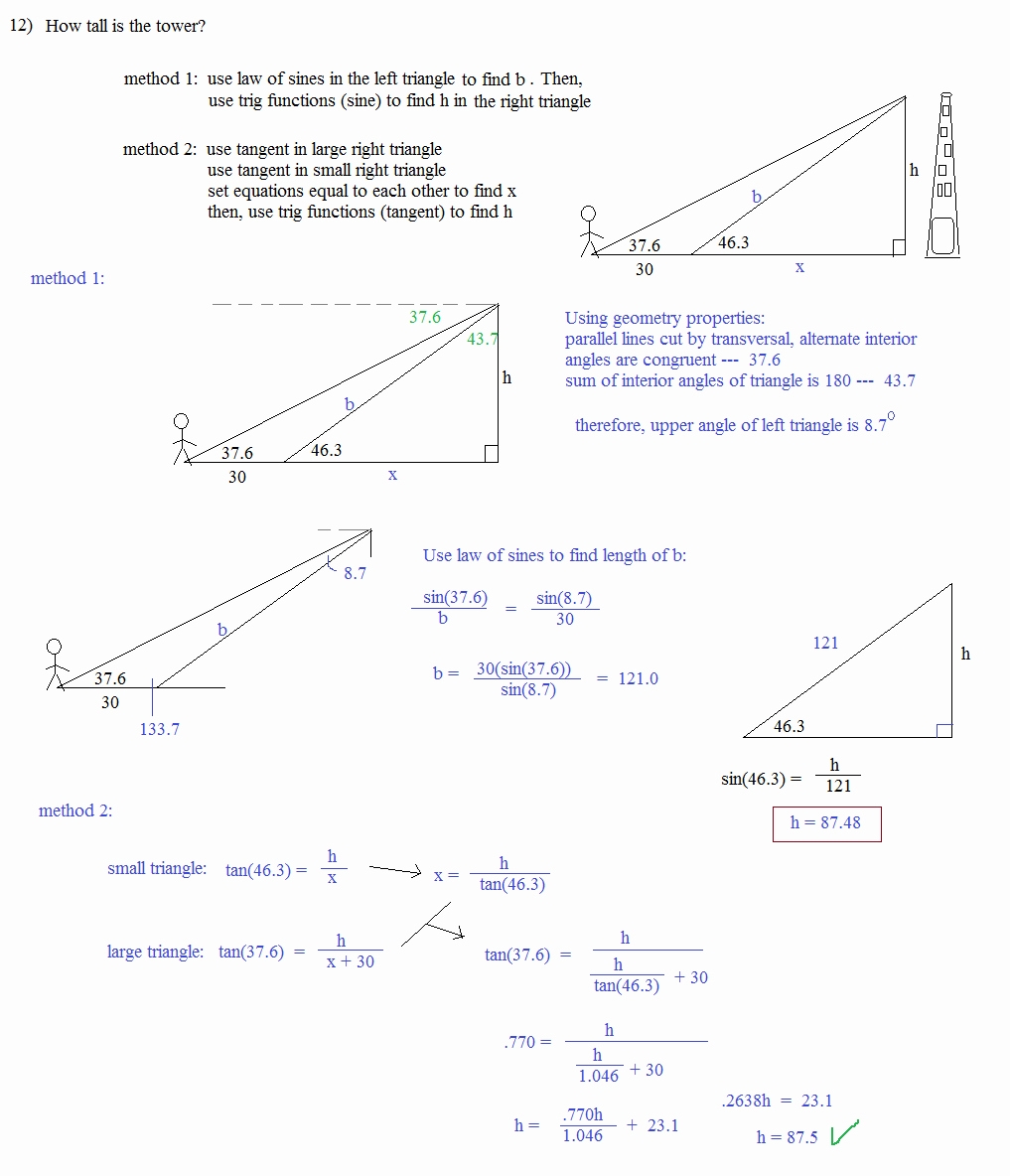
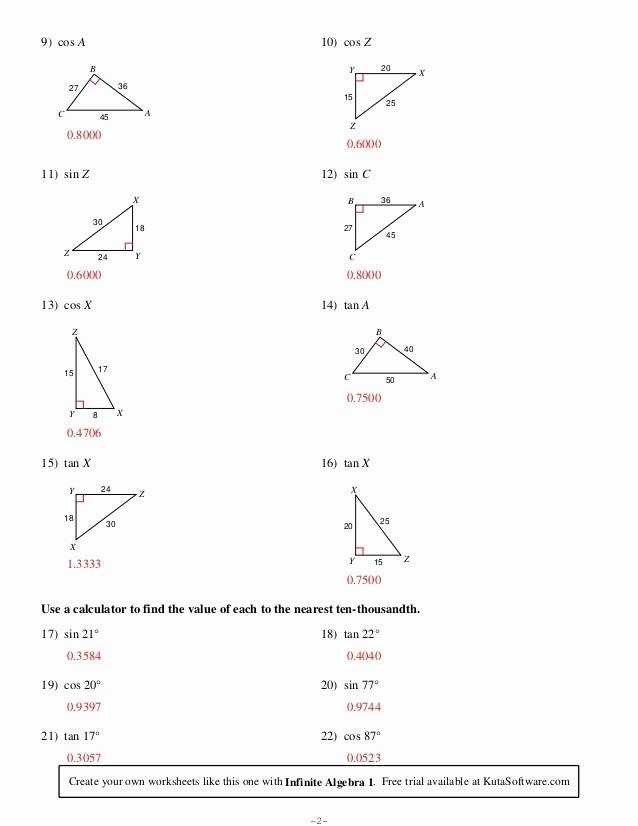
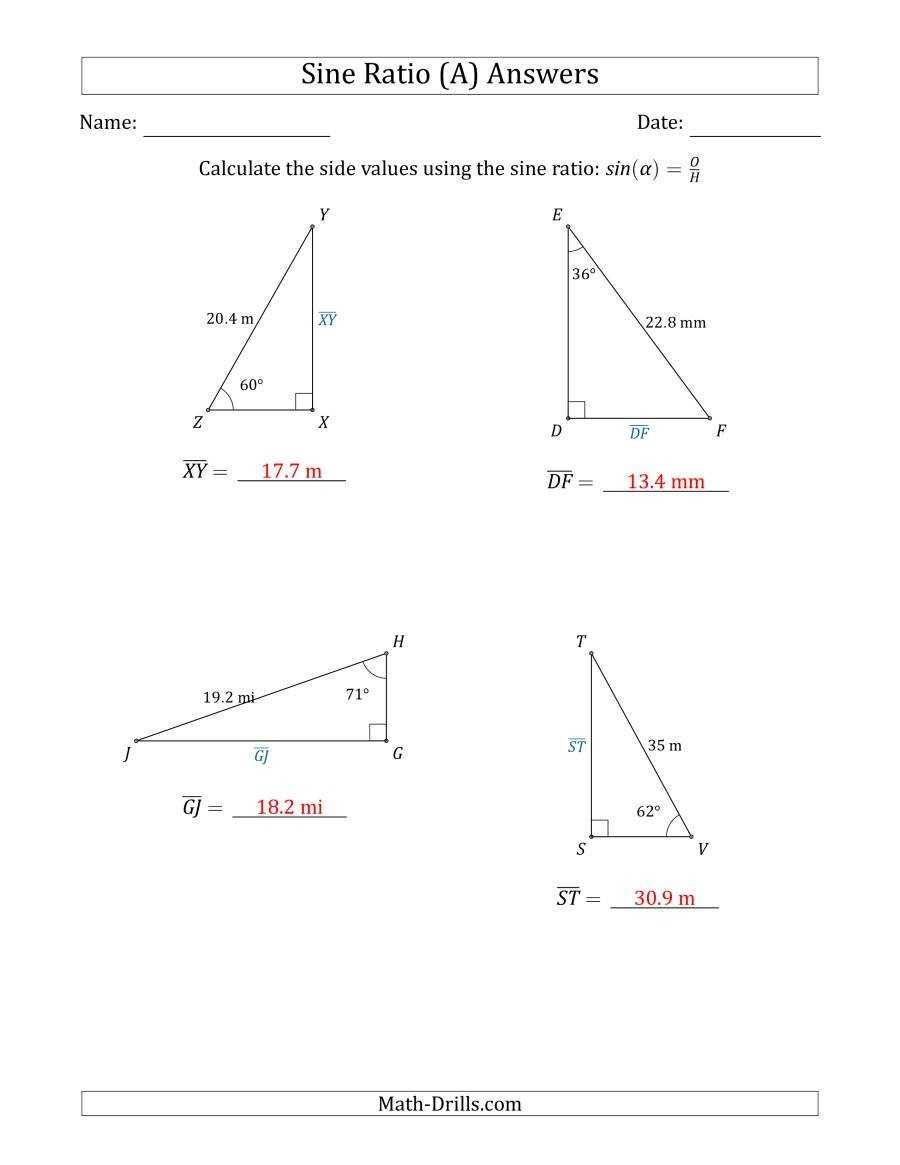
The three primary trigonometric ratios are sine, cosine, and tangent. Each of these ratios can be used to calculate the angles and sides of a triangle. The sine of an angle is equal to the ratio of the length of the opposite side to the hypotenuse. The cosine of an angle is equal to the ratio of the length of the adjacent side to the hypotenuse. Finally, the tangent of an angle is equal to the ratio of the length of the opposite side to the adjacent side.

We can use these ratios to solve for unknown variables in a triangle. For example, if we have three sides of a triangle and are looking to find the angle of one of the corners, we can use the sine ratio to calculate it. We would take the length of the opposite side and divide it by the length of the hypotenuse to get the sine of the angle. We can then use inverse sine to calculate the angle.

The Pythagorean Theorem is also an important tool when working with triangles. This theorem states that the sum of the squares of the two shorter sides of a right triangle will equal the square of the hypotenuse. This can be used to calculate the third side of a triangle when two sides are known.

Using trigonometric ratios and the Pythagorean Theorem can help us solve for angles and lengths of a triangle. These concepts are an essential part of basic geometry and algebraic equations, and understanding them is key to success in mathematics.

Breaking Down Complex Problems: Exploring Step-by-Step Solutions to Trigonometric Ratios Worksheet Answers

Trigonometric ratios are essential mathematical tools used to solve many complex problems. Therefore, it is important to have a thorough understanding of the steps involved in solving these problems. This worksheet provides a comprehensive guide to exploring step-by-step solutions to trigonometric ratios.

To start, it is important to understand the basic definitions of the primary trigonometric ratios. The three primary trigonometric ratios are sine, cosine, and tangent. Sine, or sin, is the ratio of the length of a triangle’s opposite side to its hypotenuse. Cosine, or cos, is the ratio of the length of a triangle’s adjacent side to its hypotenuse. Tangent, or tan, is the ratio of the length of a triangle’s opposite side to its adjacent side.

The next step is to identify the angle of the triangle and its lengths of side. This is usually done by using a diagram of the triangle. Once the angle and lengths of side are known, it is possible to calculate the values of the trigonometric ratios.

To calculate the values of the trigonometric ratios, it is necessary to use the trigonometric functions of sine, cosine, and tangent. These functions are found on a scientific calculator or in mathematical tables. The trigonometric functions are used to calculate the values of the trigonometric ratios.

The final step is to use the calculated values of the trigonometric ratios to solve the problem. This may involve using the ratios to calculate the angle of the triangle, the length of a missing side, or the area of the triangle.

These steps provide a comprehensive guide to exploring step-by-step solutions to trigonometric ratios. By following these steps, students can gain a better understanding of how to use trigonometric ratios in order to solve complex problems.

Examining the Impact: Exploring the Real-Life Applications of Trigonometric Ratios Worksheet Answers

Trigonometric ratios are a powerful tool for mathematics education, with implications for a variety of real-life applications. Trigonometric ratios are used to calculate angles and distances in a variety of applied settings, including surveying, navigation, and engineering.

In surveying, trigonometric ratios are used to measure angles and distances between points, allowing surveyors to accurately map out the area they are surveying. By understanding the angles and distances between points, surveyors are able to map out routes more precisely. Trigonometric ratios can also be used to calculate the size of a slope, allowing engineers to determine the best way to construct a road or bridge.

Trigonometric ratios also have applications in navigation. In order to locate a point on a map or chart, navigators use trigonometric ratios to calculate angles and distances from one point to another. This allows navigators to accurately determine their position, as well as the position of other points of interest.

In engineering, trigonometric ratios are used to calculate angles and distances between points. This information is used to design structures such as bridges and buildings. Engineers use trigonometric ratios to ensure that their designs are properly proportioned and that the structure is safe and stable.

Finally, trigonometric ratios are also used in fields such as astronomy and meteorology. Astronomers use trigonometric ratios to measure the positions of stars and planets in the sky, while meteorologists use them to track the paths of storms and other weather events.

Overall, trigonometric ratios are a powerful tool for mathematics education, with applications in a variety of real-life settings. By understanding the principles of trigonometry, students can gain a better understanding of how mathematics is used in the real world.

Conclusion

The Trigonometric Ratios Worksheet Answers provides a comprehensive and detailed look at the most important trigonometric ratios, along with some practice questions for students to test their understanding. By completing this worksheet, students will be able to demonstrate their understanding of the fundamentals of trigonometric ratios and apply their knowledge to real-world problems. Ultimately, this worksheet will help students gain a better appreciation of the importance of trigonometric ratios in mathematics.