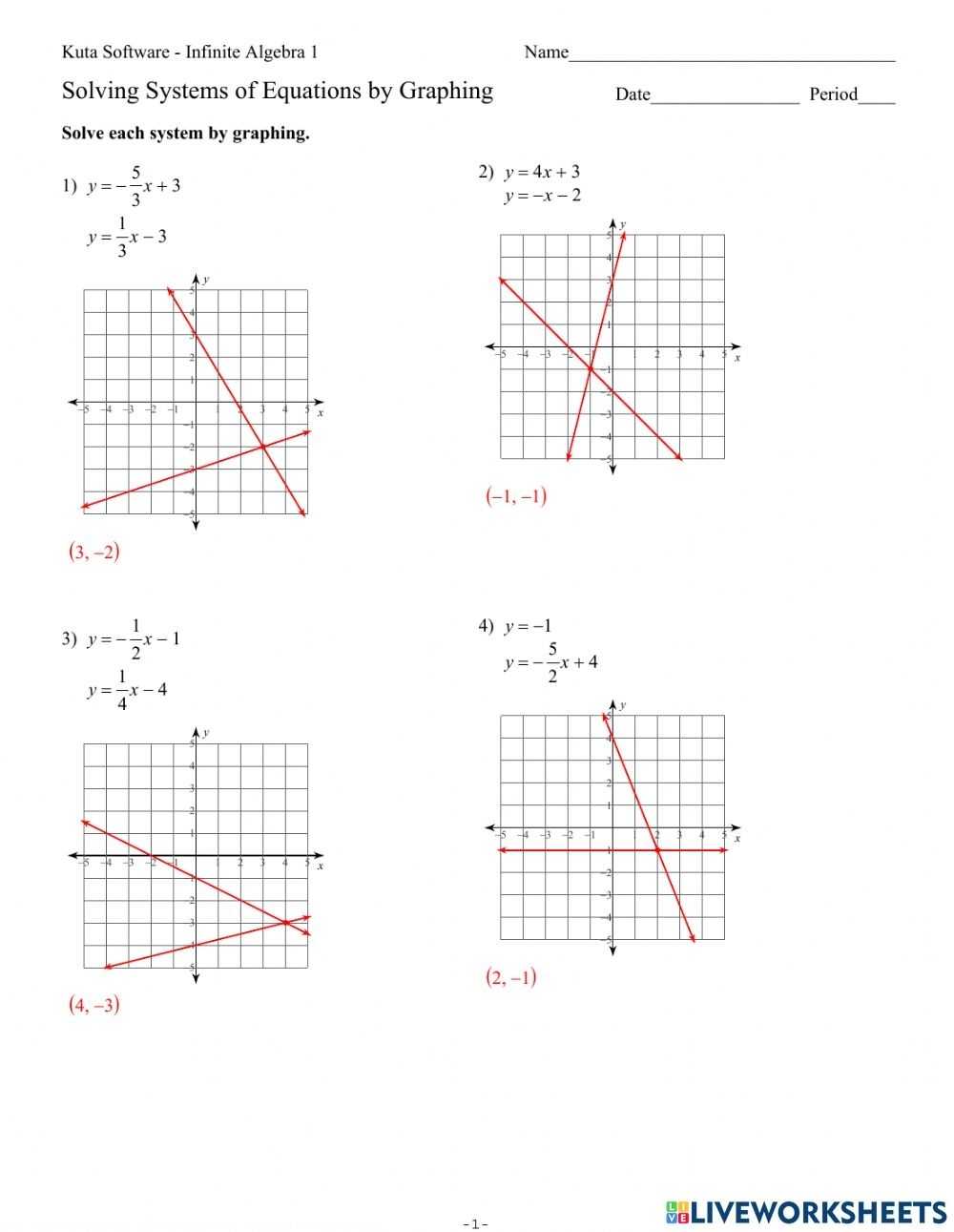
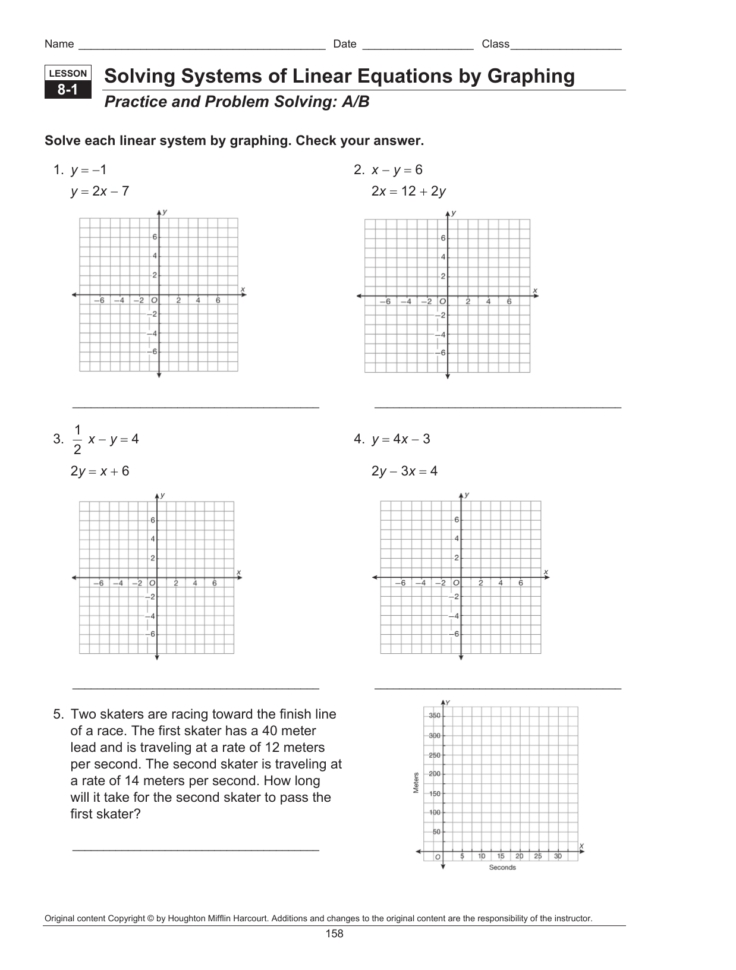
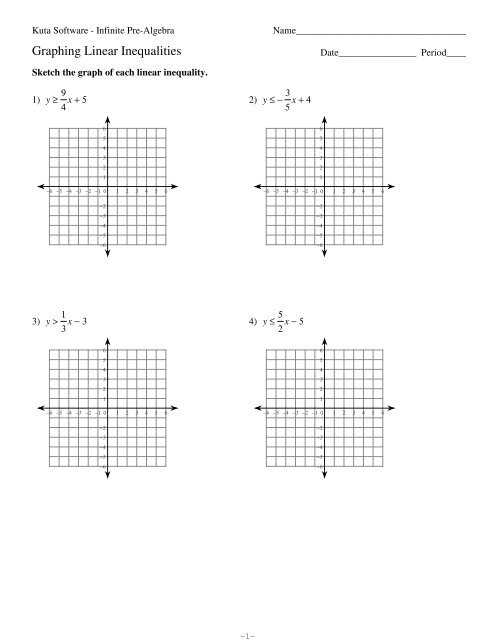
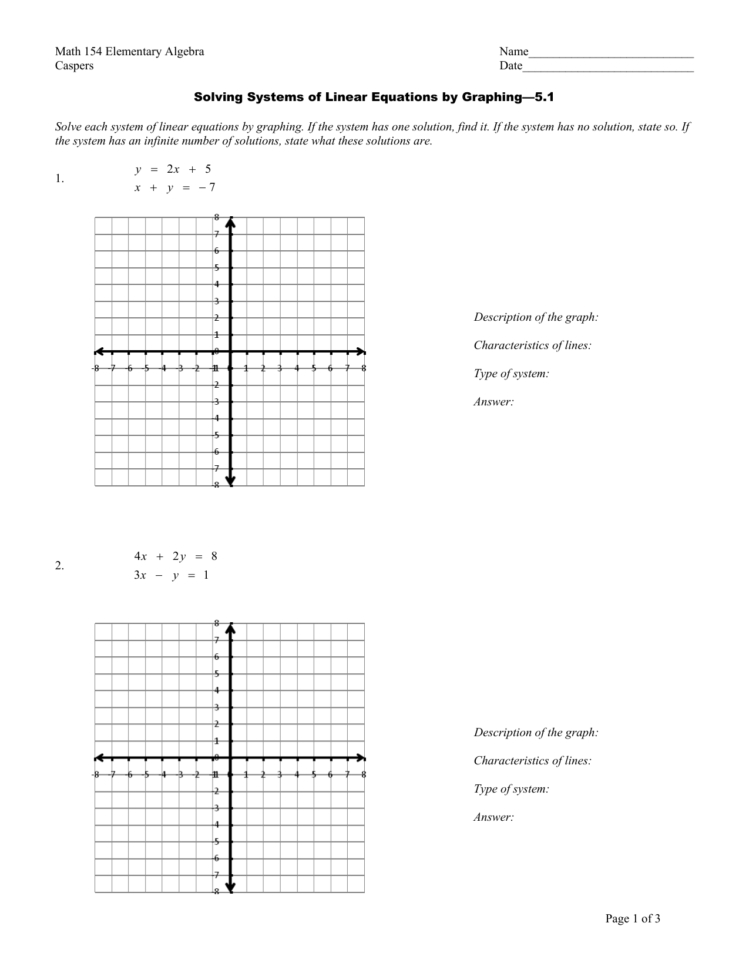
Exploring Different Types of Graphs to Solve Systems of Equations

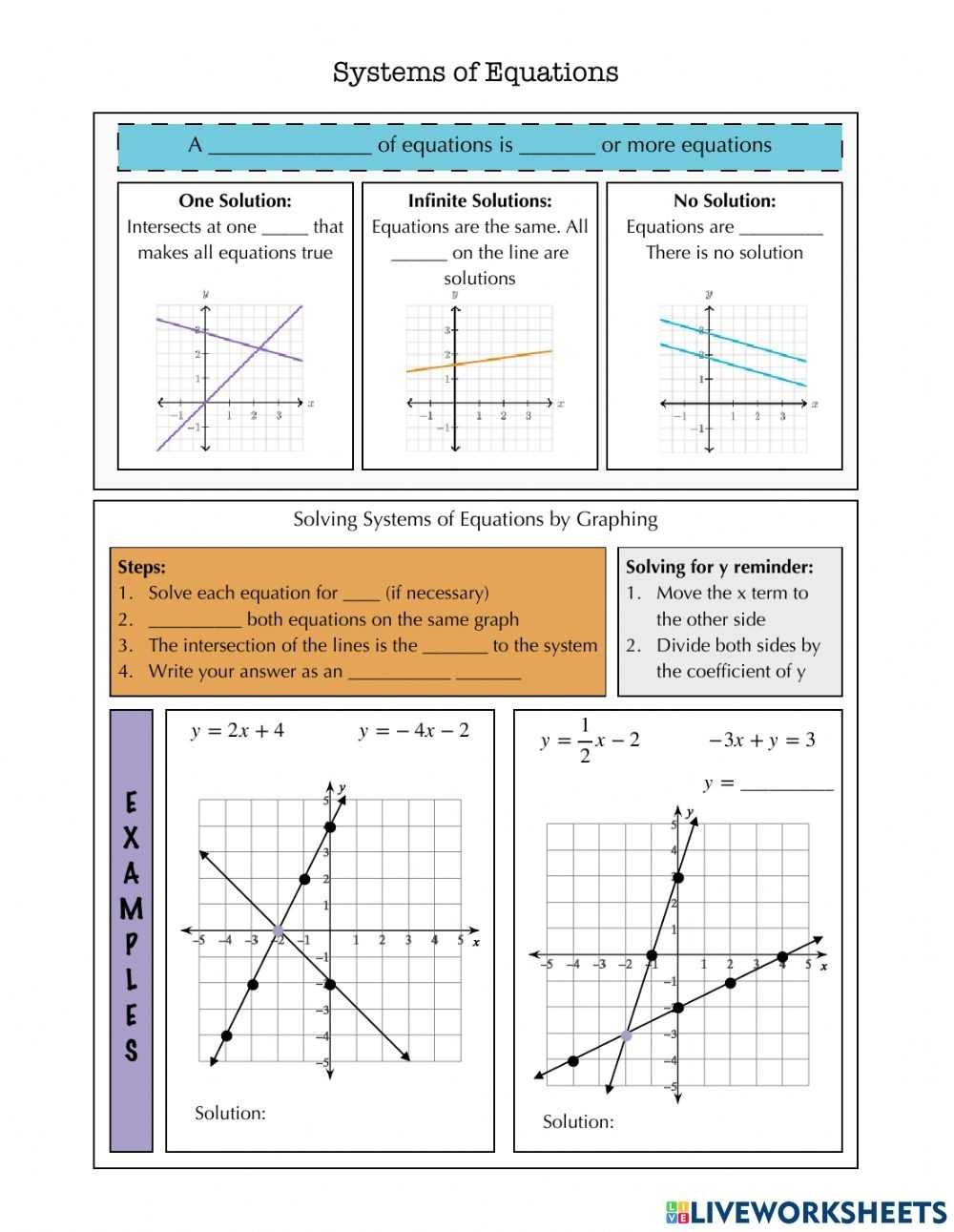
Graphical methods are an important tool for solving systems of equations. A system of equations is a set of two or more equations with the same variables. When two linear equations are graphed, the intersection of the lines is the solution to the system. Depending on the type of equations, the solution may be one, none, or an infinite number of solutions. Graphs can help us visualize and understand the different types of solutions.

There are three main types of graphs used to solve systems of equations: line graphs, circle graphs, and parabola graphs. Line graphs are a simple way to represent linear equations. When two lines are graphed, the point at which they intersect is the solution to the system. Circle graphs are used to solve systems of equations that contain a circle equation. The point at which the line and circle intersect is the solution to the system. Parabola graphs are used to solve systems that contain a parabola equation. The point at which the line and parabola intersect is the solution to the system.

Graphs are a useful tool for solving systems of equations. They provide a visual representation of the equations and their solutions. Different types of graphs can be used depending on the type of equations in the system. Line graphs are used for linear equations, circle graphs are used for systems that contain a circle equation, and parabola graphs are used for systems that contain a parabola equation. With the help of graphs, solving systems of equations can be easier and more intuitive.

How to Use a Graphing Calculator to Visualize Solutions to Systems of Equations

Visualizing solutions to systems of equations using a graphing calculator is a useful tool for understanding mathematical concepts. By plotting the equations in the form of lines or curves, it is possible to identify the points of intersection that represent the solution. To use a graphing calculator for this purpose, a few simple steps must be followed.

First, the equations must be entered into the calculator. This can be done by inputting each equation as its own statement. For example, if the system of equations is expressed as y=2x+1 and y=3x+2, the first equation should be entered as “y1=2x+1” and the second as “y2=3x+2”.

Second, the calculator must be instructed to graph the equations. This can be done by pressing the “graph” button or using the menu to select a graphing option. The calculator will then display the equations in the form of two lines or curves.

Third, the point of intersection can be identified. This is the point at which the two lines or curves meet, and is the solution to the system of equations. It is typically represented by an (x,y) coordinate pair, with the x-coordinate representing the solution for the first equation, and the y-coordinate representing the solution for the second equation.

Finally, the solution can be verified. This can be done by substituting the (x,y) coordinate pair into the original equations to make sure that the point of intersection is a valid solution. If the equations are satisfied, the point is confirmed as the solution to the system of equations.

By following these steps, a graphing calculator can be used to visualize solutions to systems of equations. This can be a helpful tool for understanding mathematical concepts and solving equations.

Making Sense of Systems of Equations Through Graphing Worksheets

Graphing systems of equations is an important skill for all students to master. In order to help students understand the principles behind graphing a system of equations, the following worksheets are designed to provide students with practice in graphing systems of equations. Each worksheet contains a variety of different equations and problems which students must solve and graph.

The worksheets are designed to provide students with an introduction to graphing systems of equations. In each worksheet, students are asked to graph a system of equations and solve for the solution. For each problem, students are given the equations and asked to graph the system. The worksheets also include questions about the solution, such as identifying the intercepts, the slope, and the equation of the line of best fit.

Graphing systems of equations is a critical skill for all students to learn. Through these worksheets, students will be able to gain a better understanding of the principles behind graphing systems of equations and will be better prepared to solve future problems.

Analyzing System of Equations Problems Through Graphing Worksheets

Graphing worksheets can be a useful tool for analyzing system of equations problems. Through the use of these worksheets, students can learn to break down and analyze problems in order to better understand them.

When working with system of equations problems, students must be able to identify the problem type, set up a system of equations, solve the equations, and interpret the solutions. Graphing worksheets can help students to practice each of these skills.

In order to set up a system of equations, students must be able to identify the equations in the problem. Graphing worksheets can help students to practice recognizing equations and setting up their own system of equations.

Once the equations have been set up, students must solve the equations. Through the use of graphing worksheets, students can practice plotting points, drawing lines, and creating a graph that accurately represents the problem. This can help students to practice the skills needed to solve a system of equations.

Finally, students must be able to interpret the solutions to their system of equations. Graphing worksheets can help students to practice this skill as they practice solving the equations. By looking at the graph, students can gain a better understanding of how the solutions relate to the equations.

Graphing worksheets can be a useful tool for helping students to analyze system of equations problems. Through the use of these worksheets, students can practice setting up, solving, and interpreting system of equations problems. As they practice these skills, students will gain a better understanding of how to solve these types of problems.

Understanding the Relationship Between Graphs and System of Equations

Graphs and system of equations have a strong relationship. Graphs are pictorial representations of equations, and equations can be used to create graphs. Graphs are very useful for visualizing relationships between variables and understanding how systems of equations interact with each other.

A graph is a collection of points in a two-dimensional plane. Each point on the graph is determined by the coordinates of the x- and y-axes. The equation of a line is typically expressed in the form y = mx + b, where m is the slope of the line, and b is the y-intercept. The slope of the line is the rate of change of the y-value for each unit change in the x-value. The y-intercept is the point at which the line crosses the y-axis.

Systems of equations are two equations that include two or more variables. They can be represented graphically by plotting the equations in a two-dimensional plane. The point at which the two lines intersect is the solution to the system of equations. If the equations are linear, the solution will be a single point, and the lines will intersect at that point. If the equations are nonlinear, the solution will be a curve, and the lines will intersect at multiple points.

The line or curve that is created by plotting the equations of a system of equations can be used to understand the relationship between the variables. For example, if the equations represent a linear system, the slope of the line will be equal to the ratio of the change in the y-value for each unit change in the x-value. This can be used to gain insight into how the variables interact with each other.

The relationship between graphs and system of equations is a powerful one. Graphs are a powerful tool for understanding the behavior of systems of equations and for visualizing their solutions. Equations can be used to create graphs, and graphs can be used to understand the behavior of systems of equations.

Incorporating Technology Into System of Equation Graphing Worksheets

Technology has become increasingly important in the teaching of mathematics and the graphing of systems of equations is no exception. With the help of technology, students are able to graph systems of equations more effectively and efficiently.

System of equation graphing worksheets can be made more engaging and interactive for students by incorporating technology into their design. For example, students can use graphing calculators or online graphing software to graph the equations for themselves. This allows them to gain a better understanding of the concepts and to practice their graphing skills.

Additionally, interactive worksheets can be created by using computer programs such as PowerPoint or Excel. These worksheets can be filled in by students and then the results can be plotted on a graph. This allows students to investigate the effects of changing the coefficients of the equations and to gain a more in-depth understanding of the concepts.

Finally, websites such as Khan Academy provide online tutorials which can be used to supplement the worksheets. These tutorials can be used to explain the concepts and to provide additional practice.

By incorporating technology into system of equation graphing worksheets, students are able to gain a deeper understanding of the concepts and to practice their graphing skills. This makes the worksheets more engaging and interactive for students, which can help to improve their understanding and performance.

Using System of Equations Graphing Worksheets to Enhance Math Skills

System of equations graphing worksheets can be a great tool for enhancing math skills. These worksheets can help students develop the ability to visualize and solve equations accurately and efficiently. By providing students with opportunities to graph equations, they are able to practice manipulating and interpreting data in a meaningful way.

System of equations graphing worksheets typically include a set of equations in two variables. Students must graph the equations and then use the resulting graph to answer questions about the equations. This helps them to understand the relationships between variables, as well as the effects that changes in one variable have on the other. By providing students with an opportunity to explore and solve equations graphically, they can gain a much deeper understanding of the mathematical concepts involved.

System of equations graphing worksheets also help students practice their problem-solving skills. As they work through each equation, they must use logic and reasoning to determine the answers. This helps them to develop the ability to think critically when presented with a problem. Through this practice, they can learn to recognize patterns and think strategically.

System of equations graphing worksheets also encourage students to think outside the box. By providing multiple ways to graph equations, students can explore different solutions without feeling limited. This encourages creativity and helps them to develop the ability to think creatively when solving complex problems.

System of equations graphing worksheets are an excellent way to enhance math skills. They provide students with an opportunity to explore equations and understand their relationships. Through this practice, students can develop problem-solving skills, as well as the ability to think creatively and strategically. By using these worksheets, students can improve their math comprehension and develop a deeper understanding of the concepts involved.

Analyzing Real-World Examples With System of Equations Graphing Worksheets

Graphing worksheets are a useful tool for analyzing real-world examples with system of equations. These worksheets provide an organized and efficient way to graphically represent data, allowing for an in-depth analysis of complex problems. By plotting points on a coordinate grid and connecting them with lines, students can quickly visualize the relationships between different variables. This visual representation can be used to understand relationships between different factors, identify patterns, and make predictions.

Graphing worksheets can be used to explore a variety of real-world examples. For instance, they can be used to analyze the impact of a change in one variable on the outcome of another. By plotting different points on a graph, students can observe how a change in one variable affects the value of another. This can be used to determine the effects of inflation on the cost of living, or the effects of changing taxes on a business’s profit.

Graphing worksheets can also be used to model physical phenomena. By plotting data points on a graph, students can observe the relationship between two variables, such as the force of a spring and its displacement. By plotting different points, students can make predictions about how a change in one variable will affect the other. This can be used to model the motion of a pendulum or the behavior of a rocket in flight.

Graphing worksheets can also be used to solve problems with multiple variables. By plotting different points on a graph, students can identify patterns and predict the impact of a change in one variable on the other. This can be used to solve problems involving fractions and equations, as well as to model the population growth of a species.

Graphing worksheets provide an efficient and organized way to represent data and analyze real-world examples with system of equations. By plotting data points on a graph, students can quickly visualize relationships between different variables, identify patterns, and make predictions. This visual representation can be used to understand relationships between different factors, and make informed decisions about complex problems.

Tips for Creating Effective System of Equations Graphing Worksheets

1. Clearly explain the concepts behind graphing equations. Be sure to include a definition of a system of equations, how to graph a linear equation, and how to interpret the points of intersection.

2. Use a variety of examples to illustrate the concepts. Include a mix of linear, quadratic, and higher order equations.

3. Provide ample space for students to practice graphing equations. Include a variety of problems on each worksheet.

4. Include questions to check comprehension and help students assess their understanding.

5. Provide step-by-step instructions on how to graph equations.

6. Provide feedback and hints to help students answer questions correctly.

7. Use visuals to help students understand the concepts. Include diagrams, illustrations, and charts where appropriate.

8. Include answer keys to help students assess their own work.

9. Make sure all equations are clearly labeled and properly formatted.

10. Use an organized, easy-to-read format.

Understanding the Nuances of Graphing System of Equations Problems

Graphing system of equations problems involve the use of two or more equations to determine the values of two unknown variables. This type of problem requires an understanding of the principles of algebra, including determining the slope of a line and the intersect of two lines. To successfully solve a graphing system of equations problem, one must be able to graph the equations and determine the point of intersection.

The first step in solving a graphing system of equations problem is to graph the equations on a coordinate plane. Once the equations are graphed, one can then identify the slope of the lines and determine if the lines are parallel, perpendicular, or neither. If the lines are parallel, then the equations have no solution. If the lines are perpendicular, then the point of intersection is the solution. If the lines are neither parallel nor perpendicular, then the point of intersection is the solution.

Once the point of intersection is determined, the coordinates of the point can be used to solve for the variables in the equations. To do this, one must substitute the coordinates of the point of intersection into the equations and solve for the variables. This will give the values of the two unknown variables.

Graphing system of equations problems can be complex. It is important to understand the principles of algebra and be able to graph equations on a coordinate plane before attempting to solve these types of problems. With practice, one can become adept at solving graphing system of equations problems.

Conclusion

The Systems of Equations Graphing Worksheet is a great tool for helping students understand how to graph equations and identify the solution of a system of equations. By working through the worksheet, students can gain a better understanding of how to use the graphing method to solve systems of equations. With this improved understanding, students can develop their skills in algebraic problem-solving and become more confident in their mathematical abilities.