Breaking Down the Basics: An Introduction to Solving Absolute Value Inequalities Worksheet

The purpose of this worksheet is to provide an introduction to solving absolute value inequalities.

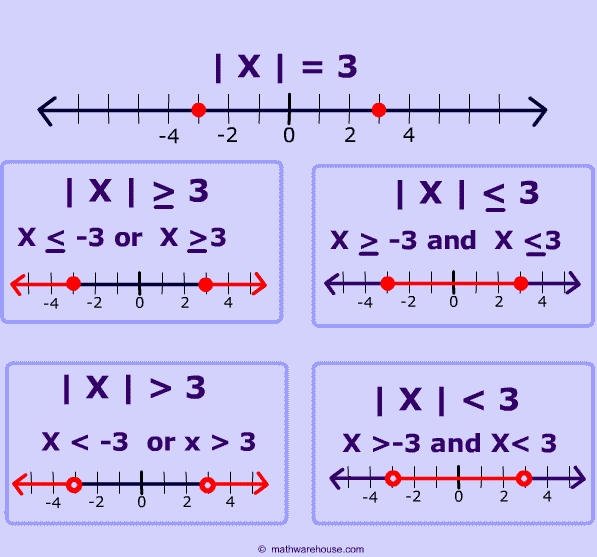
Absolute value inequalities are equations in which the variable is within an absolute value expression. They can be written as x < a or x > b, where a and b are constants. The goal of solving absolute value inequalities is to find all possible solutions for x.

In order to solve absolute value inequalities, we must first understand the structure of the expression. An absolute value expression is made up of two parts: the absolute value symbol and the contents inside the brackets. The contents inside the brackets represent the value that is being evaluated.

[toc]

To solve absolute value inequalities, we must first isolate the absolute value expression. This can be done by adding or subtracting the same value to both sides of the equation. Once the absolute value expression is isolated, we can then use the following steps to solve the equation:

1. Determine the sign of the inequality.

2. Split the equation into two cases, depending on the sign of the inequality.

3. Solve each case separately.

4. Combine the solutions from both cases to get the complete solution set.

By following these steps, we can find all possible solutions to any absolute value inequality. This worksheet will provide practice problems to help you gain an understanding of how to solve absolute value inequalities.

Mastering Absolute Value Inequalities: Advanced Techniques for Solving Worksheets

Mastering absolute value inequalities can be a daunting task, especially for advanced students. Many are familiar with the basics of solving absolute value equations, but when it comes to complex worksheets, they can quickly become overwhelmed. Fortunately, there are some advanced techniques that can help students master absolute value inequalities with ease.

The first key to success is understanding the basic concepts. Absolute value equations are equations in which the variable is always equal to the same number, regardless of its sign. This means that the variable can be either positive or negative, and the absolute value equation will remain the same. Understanding this fundamental principle is essential for success in solving absolute value inequalities.

Once the basics have been mastered, it is time to move on to the more advanced techniques. The most important of these techniques is to recognize that absolute value equations can be solved by isolating the variable. This means that the equation can be manipulated so that the variable is on one side of the equation and the expression containing the absolute value is on the other side. By doing this, the equation can be solved much more easily.

Another advanced technique for solving absolute value inequalities is to remember that the goal is to find the solution that produces the smallest absolute value possible. To do this, it is important to look at both sides of the equation. If one side of the equation produces a larger absolute value than the other side, then that side must be the solution.

Finally, mastering absolute value inequalities requires practice. Worksheets are great tools for practicing the techniques discussed above. As students become more comfortable with the concepts and techniques, solving absolute value inequalities becomes much easier. With enough practice, students will soon be able to solve even the most complex worksheets with ease.

By mastering these advanced techniques for solving absolute value inequalities, students can quickly become experts at solving worksheets. With enough practice and dedication, students can easily become masters of absolute value equations and find success in any worksheet they face.

Crafting Solutions: Tips and Tricks for Solving Absolute Value Inequalities on a Worksheet

Absolute value inequalities are an important part of algebra and can be difficult to solve. However, with a few tips and tricks, solving them on a worksheet can be made easier.

The first tip is to understand the concept of an absolute value inequality. Put simply, it is an equation involving absolute value with an inequality sign on one side. To solve such an inequality, it is necessary to identify the boundaries of the solution and then solve the equation using the appropriate methods.

The second tip is to remember the basic rules of solving absolute value inequalities. For instance, the absolute value of any number is always positive, and the sign of the inequality must always remain the same. Additionally, it is important to note that the two sides of an absolute value inequality must be considered separately.

The third tip is to use a graph to locate the solutions. A graph can be used to identify the boundaries of the solution and then used to solve the equation. This is often easier than solving the equation by hand.

The fourth tip is to double-check the answer. Before submitting the solution to the worksheet, it is important to make sure that the answer is correct. This can be done by plugging the solution into the original equation and verifying that it is indeed a solution.

Finally, when solving absolute value inequalities on a worksheet, it is important to be patient and take time to understand the concepts. Solving such equations can be tricky, and it is important to be sure that the answer is correct. With patience and understanding, solving absolute value inequalities on a worksheet can be made easier.

Conclusion

In conclusion, solving absolute value inequalities worksheet is an effective tool for helping students learn the concepts of absolute values and inequalities. It provides students with practice and reinforcement of the concepts, allowing them to become more confident in their understanding of the material. The worksheet is also a great way to help students learn how to apply the knowledge they have gained to real-world problems.

[addtoany]