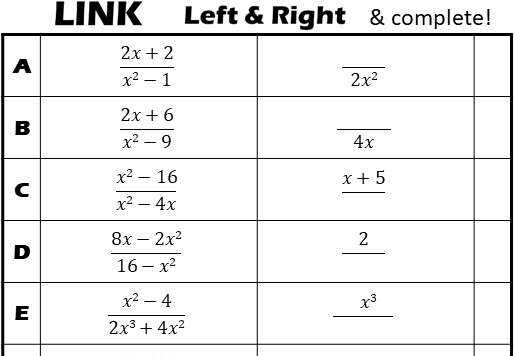
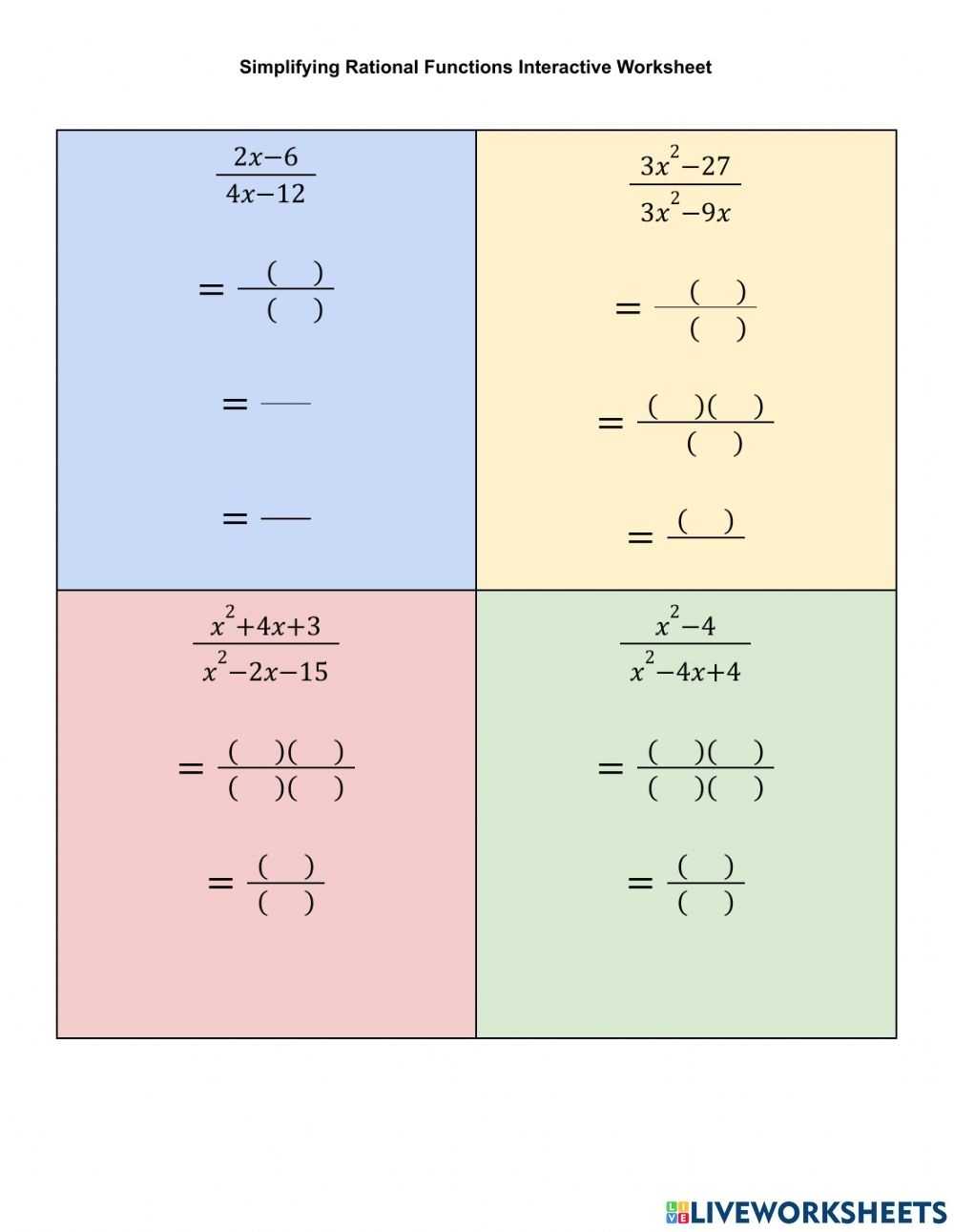
Step-by-Step Guide to Simplifying Rational Expressions Worksheet

Step 1: Gather all the materials needed for the simplifying rational expressions worksheet. This includes a pencil, calculator, and a worksheet with the rational expressions to be simplified.

Step 2: Read the instructions carefully and understand the problem. In a worksheet, there may be multiple rational expressions that need to be simplified.

Step 3: Identify any common factors between the numerator and denominator. The common factors can be removed in order to simplify the expression.

[toc]

Step 4: Factorize the numerator and denominator. If a polynomial expression is given, factorize it into its prime terms. This can be done by using the prime factorization method or the greatest common factor (GCF) method.

Step 5: Divide the numerator and denominator by their common factors. This will result in a simplified expression.

Step 6: Check the answer to ensure that it is correct.

Step 7: Repeat the steps for each of the rational expressions given in the worksheet.

Step 8: Once all the rational expressions have been simplified, the worksheet is complete.

How to Use a Worksheet to Master Simplifying Rational Expressions

Mastering the process of simplifying rational expressions can be challenging, but with a little practice and some helpful tips, it is possible to become proficient. One way to make this process easier is to use a worksheet. A worksheet is a great way to make sure that you are working through each step of the process correctly and avoiding any common mistakes.

When using a worksheet to simplify rational expressions, it is important to break down the problem into its individual components. This means that you should start by writing down the expression that you are simplifying. Be sure to label each part of the expression, such as the numerator and denominator. Once you have the expression written down, you can then begin to simplify it.

The next step is to factor the numerator and denominator. This means breaking them down into their prime factors. If the numerator and denominator have common factors, you can cross them off. This will help simplify the expression.

Once you have factored the numerator and denominator, you can then begin to reduce the expression. This means that you are looking for common factors between the numerator and denominator that can be cancelled out. For example, if the numerator and denominator both have the factor of 2, you can cancel them out and the expression will be simplified.

Finally, you should check your work to make sure that the expression is actually simplified. This is an important step, as mistakes can be easily made when simplifying rational expressions.

By using a worksheet to master simplifying rational expressions, you can ensure that you are following each step of the process correctly and avoiding common mistakes. With practice, you can become proficient in this process and make sure that your work is accurate.

Tips and Tricks for Simplifying Rational Expressions Worksheet Problems

1. Make sure to understand the meaning of the rational expression before attempting to solve it. A rational expression is a fraction, and it can be simplified by factoring and cancelling out any common factors from the numerator and denominator.

2. Utilize the distributive property. The distributive property allows you to expand terms in the numerator and denominator, making it easier to identify any common factors that can be cancelled out.

3. Utilize the greatest common factor (GCF) method. This method involves finding the greatest common factor of the numerator and denominator, then dividing both by that factor. This simplifies the rational expression.

4. Utilize the prime factorization method. This is a more complex method, but it can be used to quickly identify any common factors between the numerator and denominator.

5. Utilize the long division method. This is a more advanced method that involves dividing the numerator by the denominator and then cancelling out any common factors.

6. Utilize the additive inverse method. This method involves multiplying both the numerator and denominator by the same number, then subtracting the numerator from the denominator to produce a simplified rational expression.

7. Be sure to double-check your work. A simple mistake in the process of simplifying a rational expression can lead to incorrect results, so it is important to double-check your work before concluding.

Top 3 Reasons to Use a Simplifying Rational Expressions Worksheet

1. To Facilitate Learning: Simplifying rational expressions worksheets are a great tool for helping students learn how to solve complex equations. By providing step-by-step instructions, these worksheets help students work through the process of simplifying expressions, allowing them to gain a more intuitive understanding of the underlying concepts.

2. To Improve Problem-Solving Skills: Working through simplifying rational expressions worksheets can improve students’ problem-solving skills. By breaking down the problem into smaller, more manageable steps, students can better develop their ability to analyze and solve more difficult equations.

3. To Foster Critical Thinking: Simplifying rational expressions worksheets can help students develop critical thinking skills. By having to evaluate each step of the process and identify potential errors, students can learn how to think more deeply and analyze problems in a more meaningful way.

Conclusion

In conclusion, the Simplifying Rational Expressions Worksheet is an excellent tool for students to practice and review their skills in simplifying rational expressions. The worksheet provides the students with a comprehensive set of examples and practice questions to help them build up their understanding of the concept. With the help of this worksheet, students can better understand the process of simplifying rational expressions and become more confident in their ability to perform the process.

[addtoany]