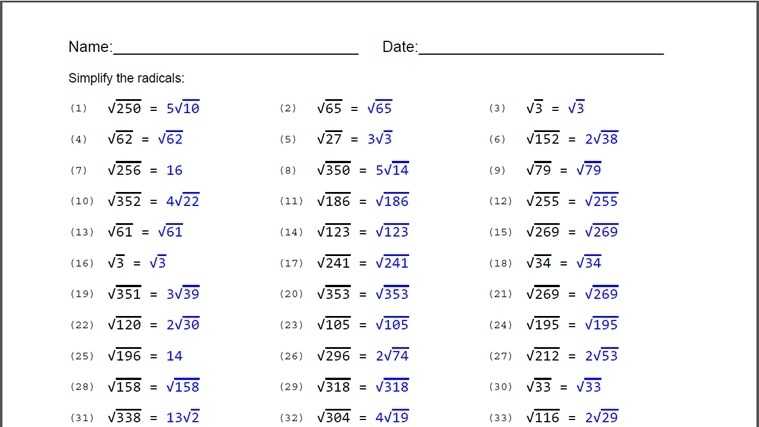
Step-by-Step Guide to Working Through Simplifying Radical Expressions Worksheet Answers
1. Begin by reading through the worksheet and understanding the instructions. Pay close attention to the order in which the expressions are to be simplified.
2. Before attempting to simplify any of the expressions, review the rules for simplifying radicals. Remember that radicals can only be simplified if the number under the radical is a perfect square. If the number is not a perfect square, it must be simplified using the conjugate method.
3. Make sure to double check your work by multiplying the simplified radical and its conjugate to ensure that the answer is correct.
[toc]
4. Take your time and work through each expression in the worksheet one at a time.
5. To simplify an expression, identify any perfect squares and square roots that can be simplified.
6. For the remaining expressions, use the conjugate method. Begin by multiplying the numerator and denominator of the radical by the conjugate of the denominator.
7. Simplify the expression, if possible, by factoring out any common factors.
8. Check your work by multiplying the simplified radical and its conjugate to ensure that the answer is correct.
9. Continue simplifying each expression in the same manner until all of the expressions are simplified.
10. Spend some time reviewing your work to ensure that all of the answers are correct.
Common Mistakes to Avoid When Simplifying Radical Expressions Worksheet Answers
1. Not Simplifying Before Adding or Subtracting: When simplifying radical expressions, it is important to simplify each radical expression before adding or subtracting them. Failure to do so can lead to an incorrect result.
2. Not Understanding the Order of Operations: In order to simplify a radical expression, it is important to use the order of operations correctly. This means that you must perform any operations inside the radical before anything outside the radical.
3. Not Distributing Before Multiplying: When simplifying radical expressions, it is important to distribute before multiplying. This means that any terms outside the radical must be multiplied by each of the terms inside the radical.
4. Not Multiplying Fractions Properly: When simplifying radical expressions, it is important to remember that fractions must be multiplied by inverting and multiplying. This means that instead of multiplying 1/2 x 3/4, you must first invert one of the fractions and multiply 3/2 x 4/3.
5. Not Recognizing Like Terms: When simplifying radical expressions, it is important to recognize any like terms. This means that if you have two terms that are the same, you can add or subtract them to simplify the expression.
6. Not Simplifying Before Raising to a Power: When simplifying radical expressions, it is important to simplify each radical expression before raising it to a power. Failure to do so can lead to an incorrect result.
7. Not Rewriting Variables in Fractional Form: When simplifying radical expressions, it is important to rewrite any variables in fractional form. This means that if you have a variable, such as y, you should rewrite it as y/1 before simplifying.
Strategies for Achieving the Best Results on Simplifying Radical Expressions Worksheet Answers
1. Carefully follow the order of operations: First, simplify any powers or roots within the expression. Next, combine any like terms. Finally, simplify any remaining radicals.
2. Carefully review each step of the simplification process. Check for any mistakes you may have made as you worked through the problem.
3. Utilize the rules of exponents and radicals to help simplify expressions.
4. When possible, factor out common terms or factors from expressions in order to simplify them.
5. Work systematically to ensure that the entire expression is simplified correctly.
6. Take your time with each step and double-check your work.
7. Utilize online tools or calculators to verify the answer you obtained.
8. If you are stuck on a problem, take a break and come back to it later with a fresh perspective.
9. Leverage online resources such as video tutorials or practice worksheets to help you become more proficient at simplifying radical expressions.
Exploring the Benefits of Using Simplifying Radical Expressions Worksheet Answers in Math Class
Math is an essential subject in any curriculum, and simplifying radical expressions is an important skill to master. Simplifying radical expressions worksheet answers provide a useful tool for helping students develop this skill. By providing students with a worksheet that contains practice problems and step-by-step solutions, they can gain the knowledge and confidence needed to solve more complex equations.
The benefits of using simplifying radical expressions worksheet answers in the math classroom are numerous. Firstly, students are able to practice their math skills by completing the worksheet. This allows them to become more familiar with the process of simplifying radical expressions, as well as develop their understanding of the necessary rules and principles that are required to solve these problems. As students gain more experience, their problem-solving skills will also improve.
In addition to the practical benefit of simplifying radical expressions worksheet answers, students can also gain a better understanding of the concept. By having the worksheet in front of them, they can take the time to think through the different steps that are needed to solve the problem. This encourages students to think critically and develop their problem-solving skills.
Furthermore, by providing students with a worksheet, they can also learn the proper syntax and formatting necessary to properly express a radical expression. In many cases, students may not be familiar with the correct syntax and formatting, which can lead to errors when attempting to solve the problem. By providing students with a worksheet, they can make sure that they are using the proper syntax and formatting to accurately express a radical expression.
Finally, simplifying radical expressions worksheet answers can also be used as a tool to help students review the material they have learned. By providing students with a worksheet that contains practice problems and solutions, they can review the material they have learned and make sure that they know how to properly apply it in the future. This helps to ensure that students are able to master the concept and become more proficient in solving equations.
In conclusion, simplifying radical expressions worksheet answers are an invaluable tool for helping students learn and master this concept in the math classroom. By providing students with a worksheet that contains practice problems and step-by-step solutions, they can gain the knowledge and confidence needed to solve more complex equations. Additionally, by having the worksheet in front of them, they can think through the different steps that are needed to solve the problem and gain a better understanding of the concept. Finally, by providing students with a worksheet, they can review the material they have learned and make sure that they know how to properly apply it in the future. All of these benefits make simplifying radical expressions worksheet answers an invaluable tool for the math classroom.
Conclusion
The Simplifying Radical Expressions Worksheet Answers provide a great resource for students to practice and develop their understanding of radical expressions. By working through the questions and answers, students will gain a better understanding of the concept of simplifying radical expressions, which can be applied to many real-world problems. With the help of this worksheet, students can increase their skills in solving radical equations and gain a deeper understanding of the subject.
[addtoany]