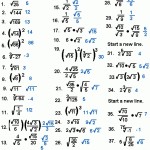How to Use a Simplifying Radical Expressions Worksheet for Quick Math Practice

Simplifying radical expressions is an important component of algebra and can be a challenging concept for students to understand. With a simplifying radical expressions worksheet, students can quickly practice and improve their math skills. Here’s how to use a simplifying radical expressions worksheet for quick math practice:

1. Begin by looking at the worksheet and familiarizing yourself with the instructions.

2. Read each question carefully and identify the equation or expression that needs to be simplified.

3. Use the rules of simplifying radicals to solve the problem.

4. Once you have solved the problem, check your answer against the answer key provided.

5. For more practice, try completing the entire worksheet.

Simplifying radical expressions worksheets are a great way for students to practice and improve their math skills. By using a worksheet, students can quickly practice and improve their knowledge of radical expressions without having to spend too much time. Additionally, this type of practice will help students develop the skills they need to solve more complex algebra problems.

10 Tips for Effectively Simplifying Radical Expressions

1. Understand the fundamentals of radical expressions: a radical is an expression that contains a square root sign and a number or variable inside the root.

2. Find the perfect square: if the number or variable inside the root is a perfect square, you can simplify the expression.

3. Identify the prime factors: if the number or variable inside the root is not a perfect square, identify the prime factors of that number or variable.

4. Group the prime factors: group the prime factors into pairs that form perfect squares.

5. Simplify the expression: use the perfect squares to simplify the expression by removing the root sign and multiplying the two factors in the perfect square together.

6. Look for common factors: look for common factors between the original expression and the simplified form of the expression.

7. Remove common factors: use the common factors to further simplify the expression.

8. Factor the remaining expression: if there are still factors that can be simplified, factor the expression into its simplest form.

9. Check your work: always check your work to make sure that the expression is in its simplest form.

10. Use the distributive property: if necessary, use the distributive property to further simplify the expression.

The Benefits of Working with Simplifying Radical Expressions Worksheets

Simplifying radical expressions worksheets can provide a wide range of benefits to students. By providing students with a variety of worksheets, they can gain a better understanding of the concepts and develop their skills in simplifying radical expressions. Here are some of the benefits of working with simplifying radical expressions worksheets:

1. Consolidate knowledge: Using worksheets to simplify radical expressions allows students to consolidate the concepts they have learned. By working through the worksheets, they are able to practice and master the techniques they need to solve the problems. This helps to ensure that they have a complete understanding of the concepts and can apply them in other settings.

2. Improve problem-solving skills: Working with simplifying radical expressions worksheets can help students to develop strong problem-solving skills. By working through the problems and applying the techniques they have learned, students can gain the confidence to solve more difficult problems. This can help them to develop their analytical skills and become better problem solvers.

3. Develop mathematical reasoning: Simplifying radical expressions worksheets can help students develop their mathematical reasoning skills. By working through the worksheets, they can gain a better understanding of how to solve problems. This can help them to develop the skills needed to think logically and solve mathematical problems.

4. Develop critical thinking skills: Working through simplifying radical expressions worksheets can also help students develop their critical thinking skills. By working through the problems and considering different approaches to solving them, students can gain insight into the problem and come up with creative solutions. This can help them to develop the skills they need to become better problem solvers and think more critically.

5. Build confidence: Working with simplifying radical expressions worksheets can also help students to build their confidence. As they work through the problems and gain a better understanding of the concepts, they can gain the confidence they need to tackle more difficult problems. This can help them to become more confident in their abilities and take on more challenging tasks.

Overall, simplifying radical expressions worksheets can provide a range of benefits to students. By providing students with a variety of worksheets, they can gain a better understanding of the concepts and develop their skills in simplifying radical expressions. This can help them to consolidate their knowledge, improve their problem-solving skills, develop their mathematical reasoning, and build their confidence.

A Comprehensive Guide to Simplifying Radical Expressions

Radical expressions are an important part of algebra. In this guide, we will discuss how to simplify radical expressions with step-by-step instructions.

First, it is important to understand the basic structure of a radical expression. A radical expression is composed of two parts: a radicand and a radical sign. The radicand is the value underneath the radical sign; this is the number that is being radicalized. The radical sign is the symbol denoting the root of the radicand.

The first step to simplifying a radical expression is to identify any perfect squares present in the radicand. A perfect square is a number that can be written as the square of another number (e.g. 4 is a perfect square because it can be written as 2^2). If any perfect squares are identified, they can be extracted from the radical and simplified.

The next step is to factor the radicand. This is done by breaking the number down into its prime factorization—that is, the prime numbers that, when multiplied together, make up the radicand. This process can be done manually or with the help of a factor tree.

The last step is to simplify the radical by using the rules of radicals. These rules state that any radicals with the same index (the number outside of the radical sign) and radicand (the value inside of the radical sign) can be combined into one radical. This means that if two radicals share the same index and the same radicand, they can be simplified by adding their indices and multiplying their radicands.

For example, if we have the radical expression √2x + √2y, we can simplify it by combining the two radicals into one radical with an index of 2 and a radicand of 2x + 2y. The simplified radical expression would be √(2x + 2y).

By following these steps, radical expressions can be easily simplified. It is important to note that while these steps may seem complicated at first, they become easier to understand with practice. With enough practice, radical expressions can be simplified without much effort.

Analyzing the Impact of the Order of Operations on Simplifying Radical Expressions

The order of operations is an important mathematical concept that is essential to accurately simplifying radical expressions. The order of operations defines a set of rules that must be followed when evaluating complex mathematical expressions. Without the order of operations, it would be difficult, if not impossible, to determine how to correctly simplify a radical expression.

The order of operations is generally expressed using the acronym PEMDAS, which stands for Parentheses, Exponents, Multiplication and Division (from left to right), and Addition and Subtraction (also from left to right). This acronym is a helpful reminder of the order in which operations should be performed when simplifying an expression.

When simplifying a radical expression, the order of operations is key to obtaining the correct answer. For example, when simplifying (4 + 2√3)2, the first step should be to calculate the square of the expression within the parentheses. If this step is omitted, the result will be incorrect. After the expression within the parentheses has been squared, the square root of the result can then be taken.

The order of operations is also essential when performing operations on multiple radicals within an expression. For example, when simplifying (2√3 + 4√2)2, the first step should be to calculate the square of each radical separately. This can be done by multiplying each radical by itself. After the squares of each radical have been calculated, the results can then be added to obtain the final answer.

In conclusion, the order of operations is a vital concept that must be taken into account when simplifying radical expressions. Without the order of operations, it would be impossible to accurately simplify an expression. It is important to remember the acronym PEMDAS and to follow it when performing operations on radical expressions.

Exploring Strategies to Simplify Radical Expressions with Multiple Terms

Radical expressions with multiple terms can be simplified by means of several strategies. Firstly, one can reduce the number of terms in the expression by combining like terms and removing any parenthesis that appear. Secondly, any numerical coefficients can be factored out of the expression; this will reduce the number of terms and simplify the expression. Thirdly, any fractional coefficients can be eliminated by multiplying by the denominator of the fraction. Finally, any terms that are perfect squares can be simplified by taking the square root of both sides of the equation.

These strategies can be used in any combination to simplify radical expressions with multiple terms. First, the expression should be examined for like terms and parenthesis, which can be combined or removed. Then, any numerical coefficients can be factored out. After that, any fractional coefficients should be eliminated. Finally, any perfect squares can be simplified by taking the square root of both sides of the equation. When all of these strategies are employed, the radical expression with multiple terms can be greatly simplified.

An Overview of the Challenges of Simplifying Radical Expressions with Variables

Simplifying radical expressions with variables can be a challenging task for students of all levels. Typically, radical expressions that contain a variable can be simplified by factoring the expression and then applying the properties of exponents and radicals. However, this may not always be an easy process, particularly if the expression contains numerous terms and variables.

For example, consider the expression √x + 6√x – 5. To simplify this expression, one must first factor the expression and then apply the properties of radicals. In this case, the expression can be factored as (√x + 5)(√x – 1). Then, applying the properties of radicals, the expression can be further simplified to √x + 5√x – 5, which is the same expression as before.

The challenge of simplifying radical expressions with variables is further complicated when the variables are raised to a power. In this situation, the expression must be factored and then the power of each term must be multiplied together and the result must be applied to each term. For example, consider the expression 4x^2√x^3. To simplify this expression, one must first factor the expression and then multiply the exponents together. In this case, the expression can be factored as (2√x)(2x√x). Then, multiplying the exponents together yields a result of 4x^3, which can then be applied to each term of the expression, resulting in a simplified expression of 8x^3.

In summary, simplifying radical expressions with variables can be a challenging task for students of all levels. Proper factoring of the expression is necessary in order to simplify the expression and applying the properties of radicals and exponents is also necessary to further simplify the expression. Furthermore, when the variables are raised to a power, the exponents must be multiplied together and applied to each term of the expression in order to simplify it.

A Step-by-Step Guide to Mastering Simplifying Radical Expressions

Simplifying radical expressions is an important skill for students to master in mathematics. It requires a thorough knowledge of the fundamental principles of algebra. This step-by-step guide will explain how to simplify radical expressions, as well as provide helpful tips and common mistakes to avoid.

Step 1: Understand the Basics of Simplifying Radical Expressions

Before attempting to simplify a radical expression, it is important to understand the basics of how they work. A radical expression is composed of a root, or a radical, and an expression inside the radical. The root is the number that is being taken the root of, and the expression is the number or variable inside the radical. The goal of simplifying a radical expression is to reduce the number of terms and roots present in the expression.

Step 2: Factor Out the Expression Inside the Radical

Once you understand the basics of radical expressions, the next step is to factor out the expression inside the radical. To do this, you must first identify the factors of the expression. Once the factors have been identified, the expression can be written as the product of the factors.

Step 3: Isolate the Radical

Once the expression inside the radical has been factored, the next step is to isolate the radical. This can be done by dividing each factor of the expression by the same number. The number being divided by must be a factor of both factors of the expression in order for the equation to remain balanced.

Step 4: Simplify the Radical

The last step in simplifying a radical expression is to simplify the radical. This can be done by breaking down the radical into its simplest form. This can be done by breaking down the radical into its prime factors and then using the rule of exponents to combine any like terms.

Helpful Tips

• Make sure to double-check your work to ensure the equation remains balanced at all times.

• Take your time when factoring and simplifying the expression.

• If you get stuck, don’t hesitate to consult a textbook or online resource for help.

Common Mistakes to Avoid

• Don’t forget to factor out the expression inside the radical before attempting to simplify it.

• Don’t forget to double-check your work to ensure the equation remains balanced.

• Don’t try to simplify a radical expression if you don’t understand how they work.

By following these steps and avoiding these common mistakes, you should be able to successfully simplify radical expressions. With practice and patience, you will soon become an expert at simplifying radical expressions.

Examining the Role of the Distributive Property in Simplifying Radical Expressions

The distributive property is a fundamental mathematical concept that is essential to understanding and simplifying radical expressions. This property states that multiplying a number by a sum of two numbers is the same as multiplying the number by each of the two numbers separately and then adding the two products together. This property can be used to simplify radical expressions by breaking the expression down into simpler parts.

For example, consider the radical expression, √18 + √20. By applying the distributive property, this expression can be rewritten as √18 + (√4 x √5). Because the square root of 4 multiplied by the square root of 5 is equal to the square root of 20, the radical expression can be further simplified as √18 + √20 = √18 + √4 x √5 = √18 + √20.

The distributive property can also be used to simplify more complex radical expressions. For example, consider the expression, (√x + √y) x (√a – √b). Applying the distributive property can simplify this expression to (√x x √a) – (√y x √b). This expression can then be further simplified by combining the radicals, resulting in √xa – √yb.

In conclusion, the distributive property is a powerful tool for simplifying radical expressions. By breaking down the expression into simpler parts, the distributive property allows for the radical expression to be simplified and rearranged into a more manageable form.

The Advantages of Using a Simplifying Radical Expressions Worksheet for Math Learning

Simplifying radical expressions is an important mathematical concept that students must understand in order to excel in higher-level mathematics. A simplifying radical expressions worksheet can be an effective tool for helping students master this concept. Here are some of the advantages of using a simplifying radical expressions worksheet for math learning.

First, a simplifying radical expressions worksheet provides a way for students to practice and hone their skills. By working through the worksheet, students can develop a better understanding of how to simplify radical expressions, and gain confidence in their ability to solve problems involving these expressions. This can lead to improved performance in math classes and tests.

Second, a simplifying radical expressions worksheet allows students to work through the steps of simplifying an expression on their own, instead of relying on their teacher’s guidance. This independence enables them to gain a better understanding of the concept and to develop their own strategies for solving problems. This can lead to increased motivation and a greater sense of accomplishment.

Third, a simplifying radical expressions worksheet can be tailored to the needs of the student. Depending on the student’s level of understanding and skill, the worksheet can be adjusted to provide more challenging problems or easier exercises. This allows the worksheet to be used by a variety of students and makes it an effective learning tool.

Finally, a simplifying radical expressions worksheet can be used to supplement traditional mathematical instruction. By providing students with an additional resource to practice their skills, they can gain a better understanding of how to solve problems involving these expressions. This can be especially beneficial for students who struggle with math or who are just starting to learn the concept.

Using a simplifying radical expressions worksheet for math learning can be a great way for students to practice their skills and gain a better understanding of this important mathematical concept. By working through the worksheet, students can develop the necessary skills to solve problems involving these expressions and improve their overall performance in math classes and tests.

Conclusion

In conclusion, simplifying radical expressions worksheet can be a powerful tool for students to practice their skills in simplifying radical expressions. It also helps students to gain a better understanding of the concept, and it can be used as an assessment tool to evaluate the students’ progress in the topic. Overall, simplifying radical expressions worksheet is an invaluable resource for students to practice and improve their understanding of this concept.