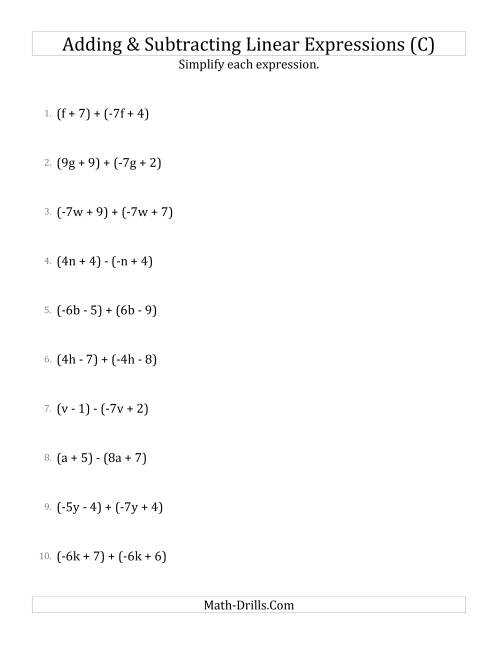Breaking Down the Basics of Simplifying Linear Expressions Worksheet
A Simplifying Linear Expressions Worksheet is a great way for students to practice and master the steps involved in solving linear equations. By completing this type of worksheet, students can learn how to use algebraic reasoning and solve linear equations in a step-by-step process.
The worksheet begins by introducing the concept of a linear equation. It then moves on to explain the process of simplifying linear expressions. This includes providing examples of how to add, subtract, multiply, and divide linear equations. The worksheet then provides practice problems for the student to complete.
The worksheet also covers basic terminology related to linear equations. This includes the definition of a variable, the concept of a coefficient, and the difference between linear and non-linear equations. Finally, the worksheet outlines the steps involved in solving a linear equation.
[toc]
The worksheet is written in a formal and descriptive writing style. This style of writing is intended to make the material easier to understand and follow. It also helps to ensure that the student understands the material presented.
The worksheet is intended to be used as a reference and teaching tool. As such, it provides students with a comprehensive overview of the steps involved in solving linear equations. This knowledge can then be applied to other problems and equations.
In conclusion, a Simplifying Linear Expressions Worksheet is a great way for students to learn and practice the steps involved in solving linear equations. This worksheet provides an overview of the material, practice problems, and an explanation of basic terminology related to linear equations. By completing this type of worksheet, students can become proficient in solving these types of equations.
How to Solve Linear Equations Using Simplifying Linear Expressions Worksheet
Solving linear equations using a simplifying linear expressions worksheet involves a few steps that can help you find the solution with ease. Firstly, identify the equation that needs to be solved. This can be done by reading the equation carefully and writing it down in standard form. The standard form of a linear equation is ax + b = c, where a, b and c are constants.
Once the equation has been written down, identify the coefficients and the constants. The coefficients are the numbers that are multiplied with the variables in the equation, while the constants are the numbers that are added or subtracted from the variables.
Once the coefficients and constants have been identified, simplify the equation. This can be done by combining like terms, that is, terms that are multiplied by the same coefficient. For example, if the equation is 3x + 4y + 5z = 7, then combine the 3x and the 4y to get 7x + 5z = 7.
After simplifying the equation, rearrange the equation so that all of the terms are on one side and the constant is on the other side. Doing so will make it easier to solve the equation. In the example given above, rearranging the equation would give 7x + 5z – 7 = 0.
Finally, solve the equation by solving for the variable. To do this, divide the coefficient of the variable by the constant on the other side of the equation. In the example given above, solving for x would involve dividing 7 on both sides of the equation, giving x = -5z/7.
Once the solution for the variable has been found, it can be checked by substituting it into the original equation. If the equation is true, then the solution is correct.
Solving linear equations using a simplifying linear expressions worksheet is an effective way of finding the solution to a linear equation in an organized manner. By following the steps outlined above, you can easily and quickly solve linear equations.
Tips and Tricks for Simplifying Linear Expressions Worksheet
1. Begin by understanding the basics of linear expressions. Linear expressions are equations that use only linear functions, or equations that involve only the operations of addition, subtraction, multiplication, and division. Make sure to understand the definitions of the basic operations and be able to identify the numerical coefficients of each term.
2. Use the distributive property to simplify linear expressions. This will help you to combine like terms and reduce the number of terms in the equation.
3. Utilize the commutative, associative, and distributive properties to simplify linear expressions. The commutative property states that the order of the terms in an expression does not matter. The associative property states that terms can be grouped together in any way when performing operations. The distributive property states that terms can be combined to create a new term.
4. Understand the order of operations. The order of operations states that you should perform operations in the following order: parentheses, exponents, multiplication, division, addition, and subtraction.
5. Simplify the equation by combining like terms. When two terms have the same variables and exponents, they can be added or subtracted together.
6. Utilize the coefficient rule. The coefficient rule states that when multiplying two terms, the coefficient of the product is equal to the product of the coefficients of the two terms. This will help you to simplify equations with multiple terms containing the same variables.
7. Use the law of exponents. The law of exponents states that when two terms with the same base are multiplied, the exponents are added. This can help you simplify equations with multiple terms containing the same variable and exponents.
8. Utilize the multiplication principle. The multiplication principle states that when two terms with the same variable are multiplied, the exponents are added and the coefficients are multiplied. This can help you simplify equations with multiple terms containing the same variable and exponents.
9. Use the power of zero. The power of zero states that any term raised to the 0th power is equal to 1. This can help you simplify equations with multiple terms containing the same variable and exponents.
10. Reduce fractions when possible. Fractions can often be reduced by dividing the numerator and denominator by the same number. This will help to make the equation simpler and easier to understand.
Common Mistakes to Avoid When Simplifying Linear Expressions Worksheet
When simplifying linear expressions, it is important to follow certain steps to ensure accuracy and avoid common mistakes. Here are some of the most common mistakes to watch out for when simplifying linear expressions:
1. Neglecting to combine like terms: One of the most common mistakes when simplifying linear expressions is neglecting to combine like terms. Like terms are terms with the same variable and exponent. Before simplifying, it is important to identify and combine any like terms in the expression.
2. Misusing order of operations: Another common mistake is misusing the order of operations when simplifying an expression. When simplifying, it is important to remember to work within parentheses first, followed by exponents, then multiplication and division, and lastly addition and subtraction.
3. Not checking for accuracy: It is important to check the simplified equation for accuracy. After simplifying an equation, use the distributive property to expand the simplified equation. If the expanded equation matches the original equation, then the simplified equation is accurate.
4. Simplifying incorrectly: When simplifying expressions with multiple terms, it is important to simplify each term correctly. This means that if one term is simplified incorrectly, the entire expression will be simplified incorrectly.
5. Neglecting to simplify: One of the most common mistakes when simplifying linear expressions is neglecting to simplify the expression. It is important to simplify the expression as much as possible to make it easier to solve.
Following these steps and avoiding these common mistakes will help ensure accuracy when simplifying linear expressions. It is important to take the time to double check your work and make sure that the simplified equation is accurate.
Different Strategies for Simplifying Linear Expressions Worksheet
The purpose of this worksheet is to provide an overview of different strategies for simplifying linear expressions. Linear expressions are mathematical equations that contain variables and constants. These expressions can be simplified by applying certain techniques and algorithms. This worksheet will discuss various strategies for simplifying linear expressions, including combining like terms, using the distributive property, and applying the properties of exponents.
Combining Like Terms
One of the simplest and most effective strategies for simplifying linear expressions is to combine like terms. This involves taking the terms with the same variable and combining them by adding or subtracting them. For example, if we have the expression 2x + 3x, we can combine the two terms by adding them together to get 5x. Similarly, if we have the expression 6x + 3 – 5x, we can combine the like terms by subtracting 5x from 6x to get x, and then adding 3 to get x + 3.
Using the Distributive Property
The distributive property is another important concept when simplifying linear expressions. This property states that when a number is multiplied by a sum or difference of two or more numbers, the product of the number and each addend can be calculated separately and then added or subtracted to get the final answer. For example, if we have the expression 3(2x + 5), we can use the distributive property to multiply 3 by each addend separately. This gives us 6x + 15, which can then be simplified to 6x + 15.
Applying the Properties of Exponents
The properties of exponents can also be used to simplify linear expressions. This involves using the rules of exponents to manipulate the expression and ultimately simplify it. For example, if we have the expression 6×2 + 3x – 5×2, we can use the properties of exponents to simplify it by subtracting 5×2 from both sides to get 6×2 – 5×2 + 3x, which can then be further simplified to x2 + 3x.
By applying these strategies, we can effectively simplify linear expressions and make them easier to understand. With practice and familiarity, these techniques can become second nature and be used to simplify even the most complex linear expressions.
A Comprehensive Guide to Simplifying Linear Expressions Worksheet
Linear expressions are a type of mathematical expression that can involve any combination of constants, variables, and operators. Simplifying linear expressions can be a daunting task for students, especially those who are new to algebra. This guide will provide an overview of the steps necessary to simplify linear expressions, including identifying constants and variables, combining like terms, and using the distributive property.
Identifying Constants and Variables
The first step in simplifying a linear expression is to identify the constants and variables in it. A constant is any number that does not change. Variables are letters used to represent an unknown or changing quantity. In an expression such as 2x + 5, the constant is 5 and the variable is x.
Combining Like Terms
Once the constants and variables have been identified, the next step is to combine like terms. Like terms are terms that have the same variable and exponent. For example, in the expression 2×2 + 3x + 4×2, the like terms are 2×2 and 4×2. To combine like terms, simply add the coefficients of the terms together. In this example, the like terms can be combined to form 6×2 + 3x.
Using the Distributive Property
The distributive property is a mathematical property that allows for the distribution of the coefficient of one term across the other terms in an expression. For example, in the expression 4x(x + 5), the coefficient of 4x can be distributed across the other terms, resulting in 4×2 + 20x. This property can be used to simplify more complex expressions.
These are the main steps for simplifying linear expressions. While it can be challenging at first, with practice, students will become more comfortable with the process and be able to quickly simplify linear expressions.
Exploring the Benefits of Simplifying Linear Expressions Worksheet
Linear expressions are mathematical equations that contain two or more variables. They can be used to represent complex relationships between variables and to solve a variety of problems. Simplifying linear expressions is a useful way to reduce the complexity of the expression and make it easier to work with.
Exploring the benefits of simplifying linear expressions can be beneficial for anyone looking to increase their understanding of math. Simplifying an expression can help to make it easier to read and understand, and can also help to reduce the amount of time needed to solve a problem. By simplifying a linear expression, it can be broken down into simpler parts, which can then be used to quickly and accurately solve problems.
Simplifying linear expressions can also allow for a better understanding of the relationships between the variables in the equation. By breaking the linear expression down into simpler parts, it can be easier to visualize the effects of one variable on the other. This can be especially helpful when solving equations that involve multiple variables. In addition, simplifying an expression can make it easier to identify errors or oversights when solving a problem.
Finally, simplifying linear expressions can also make it easier to compare two or more expressions. By breaking the expressions down into their individual components, it can be easier to spot similarities and differences between them. This can be especially helpful when trying to solve a problem that requires multiple equations.
In conclusion, simplifying linear expressions can provide a range of benefits for anyone looking to increase their understanding of math. It can help to reduce the complexity of an expression, make it easier to read and understand, simplify the process of solving a problem, and make it easier to identify errors or oversights. In addition, it can help to visualize the relationships between the variables in an equation, and it can also make it easier to compare two or more expressions.
Creative Approaches to Simplifying Linear Expressions Worksheet
Linear expressions can be complex and confusing for students to understand. However, there are several creative approaches to simplifying these expressions that can make them more accessible and easier to work with.
One approach is to break the expression into smaller pieces. This means breaking the expression down into its components and looking at each part separately. By doing this, students can identify what each piece of the expression represents and understand how it fits into the larger equation.
Another approach is to use visual elements. Visual elements can help students to make sense of linear expressions by providing concrete representations of the various terms and operations that are involved. For example, diagrams, charts, and graphs can provide visual cues that make the expression easier to comprehend.
A third approach is to use manipulatives. Manipulatives are physical objects that can be used to represent linear expressions. For example, students can use blocks, tiles, or other objects to represent each term or operation that is part of the expression. By manipulating these manipulatives, students can begin to understand how the expression works.
Finally, students can use technology to simplify linear expressions. There are many apps and websites that can help students to visualize linear expressions and provide step-by-step solutions. These tools can make simplifying linear expressions much easier and can help students to develop a deeper understanding of the material.
By using these creative approaches, students can gain a better understanding of linear expressions and learn how to simplify them more effectively. With the right techniques and tools, linear expressions can be made much more accessible and easier to work with.
Working Through Examples of Simplifying Linear Expressions Worksheet
Simplifying linear expressions is an important part of algebra. In order to understand how to simplify expressions, it is helpful to work through examples. This worksheet provides an opportunity to practice simplifying linear expressions.
Each expression in this worksheet contains a combination of addition, subtraction, multiplication, and division. To simplify each expression, use the order of operations: parentheses, exponents, multiplication and division (from left to right), and addition and subtraction (from left to right).
For example, consider the expression 5x + 2 – 3x. To simplify this expression, start by subtracting 3x from both sides. This results in 2x + 2. Next, subtract 2 from both sides, resulting in the simplified expression 2x.
In another example, consider the expression 5x + 2 – 3x + 5. Begin by subtracting 3x from both sides, yielding 2x + 2 + 5. Next, add 5 to both sides, resulting in 2x + 7. Finally, subtract 7 from both sides to obtain the simplified expression 2x.
By working through these examples and following the order of operations, students can practice simplifying linear expressions. With practice, they will be able to simplify more complex expressions.
Understanding the Fundamentals of Simplifying Linear Expressions Worksheet
The ability to simplify linear expressions is a skill that is essential for students studying mathematics. Understanding the fundamentals of simplifying linear expressions will help students master this important skill.
The first step to simplifying linear expressions is to identify the terms and coefficients. Terms are the individual numbers and symbols, such as 3x or 5y, that make up an expression. Coefficients are the numerical values of the terms. Once these have been identified, the second step is to combine like terms. This involves combining terms that have the same variable, such as 3x and 5x, and adding their coefficients together.
The third step is to factor out any common factors. This means looking for terms that contain the same numerical values and variables. For example, 2x and 4x both contain the same variables, so they can be combined by factoring out the common factor of 2.
The fourth step is to reduce the expression to its simplest form. This means removing any numerical factors that are not essential to the expression. Factors that can be removed include any numbers that are divisible by the coefficients of the other terms, as well as any numerical terms that are equal to one.
By following these steps, students can easily simplify linear expressions. Understanding the fundamentals of simplifying linear expressions is an important part of mastering this skill. With practice, students will be able to more easily simplify linear expressions and improve their overall mathematics skills.
Conclusion
The Simplifying Linear Expressions Worksheet is a great way to practice and reinforce basic math skills. It is also a good way to learn and understand the concept of simplifying linear expressions. With the worksheet, students can practice and apply the concepts learned in class. By completing the worksheet, students can gain a better understanding of linear equations and can apply these concepts to solve practical problems.
[addtoany]