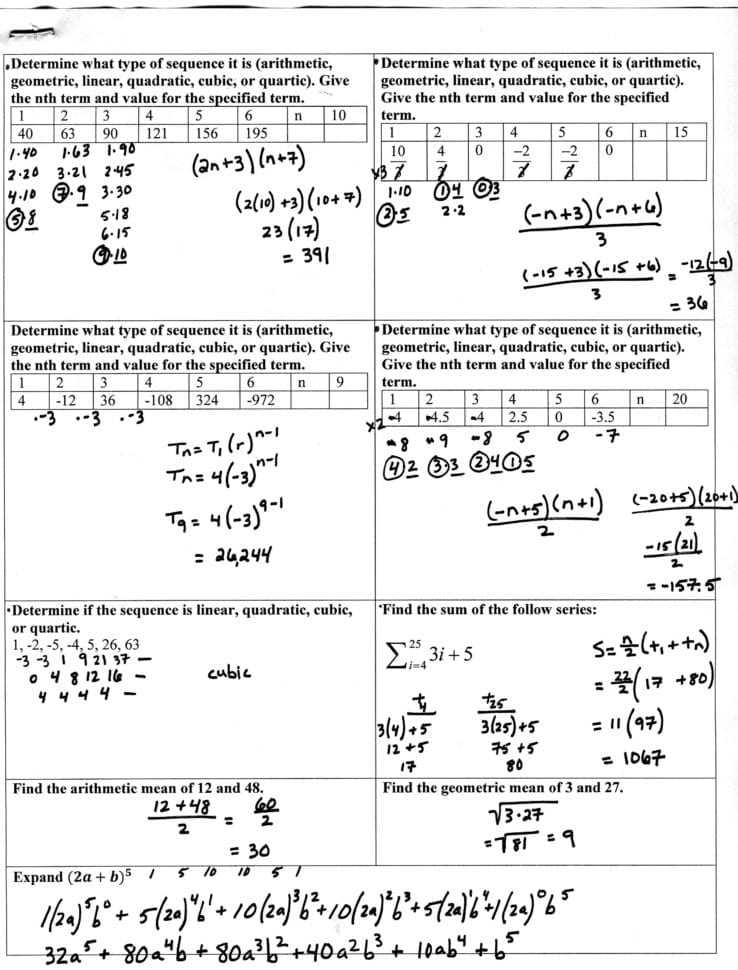
Understanding Sequences And Series: A Step-By-Step Guide To Finding The Answers to Your Worksheet
Sequences and series are an important part of mathematics and understanding them can help you solve a variety of problems. A sequence is a set of numbers that are related in some way, such as by a pattern or by a formula. A series is the sum of a sequence of numbers. This step-by-step guide will help you understand sequences and series, so you can confidently solve your worksheet questions.
Step 1: Identify the Sequence or Series.
When you first look at a sequence or series question, it is important to identify what type of problem you are dealing with. Look for keywords such as “sum,” “term,” or “pattern” to determine if the question is asking about a sequence or a series.
Step 2: Understand the Pattern.
Once you have identified the sequence or series, it is important to understand the pattern that is being used. For example, if the question is about a sequence, there may be a pattern of increasing or decreasing numbers, or a pattern of adding a certain number each time.
[toc]
Step 3: Write Out the Terms of the Sequence or Series.
Once you understand the pattern, it is time to write out the terms of the sequence or series. This will help you visualize the pattern and make it easier to find the answer.
Step 4: Find the Answer.
Once you have written out the terms of the sequence or series, you can use different methods to find the answer. Depending on the type of problem, you may be able to use algebraic methods, geometric methods, or even a calculator.
Step 5: Check Your Answer.
Once you have found the answer, it is important to check it to make sure you have the correct solution. Depending on the type of problem, you may need to use a calculator or perform a test to ensure that your answer is correct.
By following these steps, you can confidently solve your worksheet questions about sequences and series. With practice and patience, you will be able to understand and apply the concepts of sequences and series to solve a variety of problems.
Exploring Different Types of Sequences And Series: An In-Depth Look At What Each Type Entails
Sequences and series are the two main types of mathematical patterns. A sequence is a pattern of numbers or objects that follow a particular order. The order is usually based on a mathematical rule, such as addition, multiplication, or subtraction. A series is a sum of the terms in a sequence. It is usually used to analyze the behavior of a sequence as it approaches infinity.
One of the most common types of sequences is the arithmetic sequence. An arithmetic sequence is a sequence in which each term is obtained by adding a fixed number, called the common difference, to the preceding term. For example, the sequence 1, 3, 5, 7,… is an arithmetic sequence because each term is obtained by adding two to the preceding term. Similarly, the sequence 4, 7, 10, 13, … is an arithmetic sequence because each term is obtained by adding three to the preceding term.
Another common type of sequence is the geometric sequence. In a geometric sequence, each term is obtained by multiplying the preceding term by a fixed number, called the common ratio. For example, the sequence 1, 2, 4, 8, … is a geometric sequence because each term is obtained by multiplying the preceding term by two. Similarly, the sequence 1, 3, 9, 27, … is a geometric sequence because each term is obtained by multiplying the preceding term by three.
A Fibonacci sequence is another type of sequence. It is a sequence in which each term is the sum of the two preceding terms. For example, the sequence 1, 1, 2, 3, 5, 8, … is a Fibonacci sequence because each term is the sum of the two preceding terms.
A harmonic sequence is yet another type of sequence. In a harmonic sequence, each term is the reciprocal of the preceding term. For example, the sequence 1, ½, ¼, ⅛, … is a harmonic sequence because each term is the reciprocal of the preceding term.
The sum of the terms in a sequence is known as a series. Series are often used to analyze the behavior of a sequence as it approaches infinity. The most common type of series is the geometric series. In a geometric series, each term is obtained by multiplying the preceding term by a fixed number, called the common ratio. The sum of the terms of a geometric series approaches infinity if the common ratio is greater than one.
The sum of the terms of an arithmetic series can also be calculated. An arithmetic series is a series in which each term is obtained by adding a fixed number, called the common difference, to the preceding term. The sum of the terms of an arithmetic series approaches infinity if the common difference is positive and is finite if the common difference is negative.
In conclusion, there are several different types of sequences and series. Arithmetic, geometric, Fibonacci, and harmonic sequences are some of the most common types of sequences. Similarly, geometric and arithmetic series are some of the most common types of series. Understanding the different types of sequences and series can help mathematicians analyze the behavior of a sequence as it approaches infinity.
How To Use Sequences And Series To Solve Problems: A Step-By-Step Tutorial On How To Utilize These Concepts
Sequences and series are powerful mathematical tools that can be used to solve a wide range of problems. A sequence is a set of numbers that follows a particular pattern, while a series is a sum of the numbers in a sequence. By understanding these concepts and how to use them, you can solve many complex problems. This tutorial will guide you through the basics of how to use sequences and series to solve problems.
Step 1: Understand the Problem
Before attempting to solve a problem with sequences and series, it is important to first understand the problem. Read the problem carefully and make sure you understand what it is asking you to do. Identify any given information, such as the terms in the sequence or series, and any parameters that need to be satisfied.
Step 2: Identify the Type of Sequence or Series
Once you have understood the problem, you need to identify the type of sequence or series you are dealing with. There are several types of sequences and series, such as arithmetic, geometric, and harmonic. Each type of sequence or series has its own set of rules and characteristics.
Step 3: Calculate the Terms in the Sequence or Series
Once you have identified the type of sequence or series, you can calculate the terms in the sequence or series. Depending on the type of sequence or series, the calculation of each term will be different. For example, in an arithmetic sequence, each term is equal to the previous term plus a constant. In a geometric sequence, each term is equal to the previous term multiplied by a constant.
Step 4: Find the Sum of the Sequence or Series
Once you have calculated the terms in the sequence or series, you can find the sum of the sequence or series. Depending on the type of sequence or series, different formulas or techniques can be used to calculate the sum. For example, in an arithmetic sequence, the sum of the sequence is equal to the average of the first and last terms multiplied by the number of terms in the sequence.
Step 5: Solve the Problem
Once you have calculated the sum of the sequence or series, you can use the sum to solve the problem. In some cases, you may only need to use the sum to answer the question. In other cases, you may need to do further calculations or use other techniques to solve the problem.
By following these steps, you can learn how to use sequences and series to solve problems. With practice and a good understanding of the concepts, you can become an expert at solving problems with sequences and series.
Common Mistakes To Avoid When Working With Sequences And Series: Tips And Tricks To Help You Get The Right Answers
1. Not accounting for the difference between arithmetic and geometric sequences: One of the most common mistakes when dealing with sequences and series is not recognizing the difference between arithmetic and geometric sequences. Arithmetic sequences involve a common difference between successive terms, while geometric sequences involve a common ratio between successive terms. Failing to distinguish between the two can lead to incorrect answers.
2. Not understanding the concept of limit of a sequence: Another common mistake is not understanding the concept of a sequence’s limit. The limit of a sequence is the value that the terms of the sequence tend towards as the number of terms increases. Understanding the concept of limit can help you determine the sum of an infinite sequence.
3. Not recognizing the pattern in a sequence: Many sequences follow a certain pattern. Recognizing the pattern in a sequence can help you find the next term in the sequence or the sum of the terms in the sequence. If you can identify the pattern, you can use it to determine the answer instead of having to calculate it.
4. Not understanding the properties of a series: When dealing with series, it is important to understand the properties of the series. Properties such as the sum of the terms, the number of terms, the type of series, and the order of the series can help you determine the answer to a series problem.
5. Not recognizing the difference between convergent and divergent series: It is also important to understand the difference between convergent and divergent series. Convergent series converge to a specific value as the number of terms increases, whereas divergent series do not converge to any specific value. Recognizing the difference between these two types of series can help you determine the answer to a series problem.
By understanding and applying the tips and tricks listed above, you can avoid common mistakes when working with sequences and series and get the right answers.
The Benefits of Learning Sequences And Series: Tips On How To Make The Most Of Your Worksheet Answers
Learning sequences and series can help students to build a strong foundation for advanced math topics. Sequences and series provide students with an understanding of patterns and how to apply them to solve a variety of math problems. By learning sequences and series, students can develop a better understanding of math concepts and how to apply them to their studies.
To make the most of your worksheet answers, it is important to focus on the key concepts and principles related to sequences and series. This will help you to understand the patterns and relationships between the different elements of the sequence or series. Additionally, it will help you to identify mistakes or gaps in reasoning and work through them.
When working through worksheet answers, it is also important to think critically and analyze the data. This will help you to gain a better understanding of the sequence or series and the relationships between different elements. Additionally, it will help you to identify areas where further exploration may be needed.
Practice is also important to ensure that you are able to apply the concepts you have learned to answer questions correctly. This practice should include both simple and complex problems. As you become more comfortable with sequences and series, you can then begin to apply the concepts to more challenging questions.
Finally, it is important to keep track of your progress with each worksheet answer. This will help you to identify areas where you need to focus and areas that you have already mastered.
By following these tips, you can make the most of your worksheet answers and develop a strong understanding of sequences and series. With this knowledge, you will be better equipped to answer difficult questions and apply the concepts to a variety of math problems.
Sequences And Series: A Comprehensive Guide To Knowing The Different Types And How To Utilize Them
Sequences and series are powerful mathematical tools that can be used to analyze and predict patterns in a variety of fields. In mathematics, a sequence is an ordered list of elements that may or may not follow a certain pattern. A series is the sum of the terms in a sequence.
There are several types of sequences and series commonly used in mathematics. Arithmetic sequences are sequences in which the difference between two consecutive terms is the same. For example, the sequence 1, 3, 5, 7, 9, 11 is an arithmetic sequence because the difference between each consecutive term is 2. Geometric sequences are sequences in which each term is a fixed multiple of the one before it. For example, the sequence 1, 2, 4, 8, 16 is a geometric sequence because each term is double the term before it.
Fibonacci sequences are a type of sequence in which each term is the sum of the previous two terms. For example, the sequence 1, 1, 2, 3, 5, 8, 13 is a Fibonacci sequence because each term is the sum of the previous two terms. Other types of sequences include the Taylor series, power series, and exponential sequences.
Once a sequence or series is identified, it can be used to make predictions or analyze certain patterns. For example, an arithmetic sequence can be used to predict future terms of a sequence and to calculate the sum of a sequence up to a certain term. A geometric sequence can be used to predict future terms and to calculate the sum of a sequence up to a certain term. The Fibonacci sequence can be used to calculate the sum of the first n terms and to calculate the nth term of a sequence.
In addition, certain sequences and series can be used to solve various mathematical problems. For example, the Taylor series can be used to approximate the value of a function at a specific point, while power series can be used to solve differential equations. Exponential sequences can be used to calculate growth rates and compound interest. By mastering the use of sequences and series, one can gain a better understanding of many mathematical concepts.
Tips To Help You Understand The Complexity Of Sequences And Series: A Complete Overview Of The Different Types And How To Use Them
Sequences and series are mathematical concepts that have been used for centuries to study and analyze patterns. They are defined as a set of numbers that follow a certain pattern. A sequence is a list of numbers that follow a particular order, while a series is the sum of all the numbers in a sequence. The types of sequences and series vary, and each type has its own unique properties and characteristics.
The most common type of sequence is an arithmetic sequence. This type of sequence has a constant difference between each term. For example, the sequence 2, 4, 6, 8, 10 is an arithmetic sequence because each term is two more than the previous term. Other types of sequences include geometric sequences, which have a constant ratio between each term, and Fibonacci sequences, which follow a particular pattern.
Series are the sums of all the terms in a sequence. There are two types of series: finite and infinite. A finite series has a set number of terms and the sum of those terms can be calculated. An infinite series has an unlimited number of terms and the sum of those terms cannot be calculated.
Sequences and series can be used to solve a variety of mathematical problems. For example, they can be used to calculate the number of terms in a sequence, or to find the sum of an infinite series. They can also be used to analyze data, such as analyzing the growth of a population over time.
Understanding sequences and series is essential for any student studying mathematics. Knowing the different types of sequences and series, as well as how to use them, can help students gain a deeper understanding of mathematics and be better prepared for more advanced mathematics courses.
Learning How To Interpret Answers To Sequences And Series Worksheets: The Benefits Of Doing So For Your Future Math Studies
Learning how to interpret answers to sequences and series worksheets is an essential skill to have when studying mathematics. In mathematics, sequences and series are used to describe a pattern of numbers, symbols, or objects. Knowing how to interpret the answers to these worksheets can help students to make sense of the mathematical concepts they are studying.
The ability to interpret the answers to sequences and series worksheets can benefit students in a number of ways. First, it can help them to better understand the concepts that they are studying. By understanding the answers to these worksheets, students can better comprehend the underlying mathematics behind the problem. Additionally, this knowledge can help them to develop better problem-solving skills as they will be able to recognize patterns and make use of them when solving equations.
Second, learning how to interpret the answers to sequences and series worksheets can help students to improve their test scores. Knowing how to interpret the answers to these worksheets can help students to better recognize the patterns that are being tested on standardized tests or other exams. This can help them to better prepare for these tests and improve their scores.
Finally, learning how to interpret the answers to sequences and series worksheets can help students to better understand more advanced topics in mathematics. By having a better understanding of the patterns and relationships of numbers, symbols, and objects, students can better understand the more complex mathematics that they encounter in advanced mathematics classes. This can help them to better understand the concepts and gain a better grasp of the material that they are studying.
Learning how to interpret the answers to sequences and series worksheets can benefit students in many ways. It can help them to better understand the concepts they are studying, improve their test scores, and gain a better understanding of more advanced topics. As such, it is an essential skill to have when studying mathematics.
Conclusion
The Sequences and Series Worksheet Answers provide an excellent resource for students to explore the concepts of sequences and series. Through the use of the answers provided, students can better understand the underlying principles of the topics and gain a deeper understanding of the material. With this knowledge, students can use the worksheet to further their mathematical understanding and develop the skills needed to work with sequences and series in the future.
[addtoany]