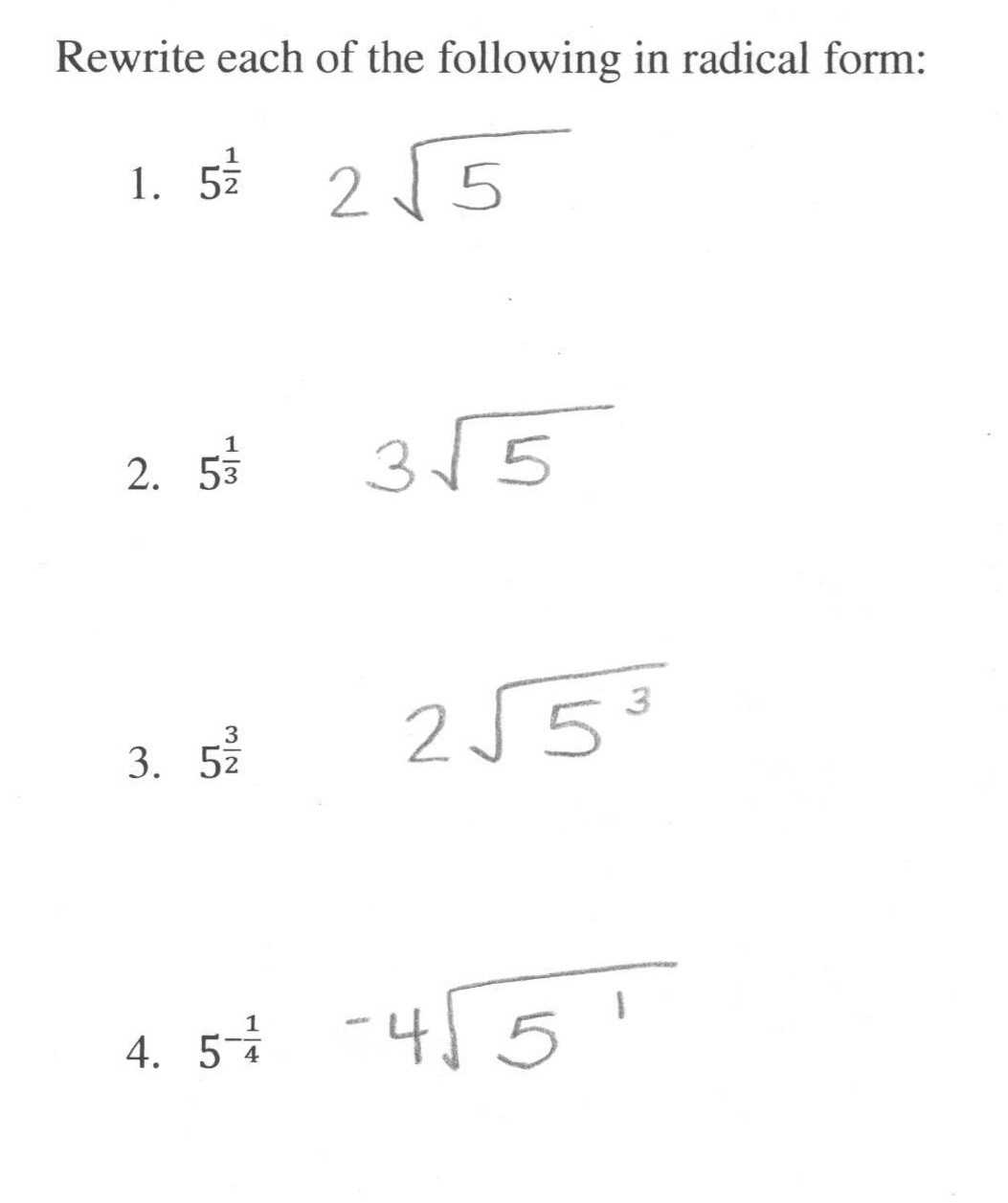Exploring Radicals and Rational Exponents: How to Tackle the Worksheet with Ease

Radicals and rational exponents are mathematical concepts that can be intimidating to tackle. However, with the right guidance and understanding, tackling them on a worksheet can be a matter of ease.

To start, it is important to understand the basics of radicals and rational exponents. Radicals are the root of a number or expression, indicated by the symbol √. Rational exponents are the power to which a number is raised, indicated by the symbol ^. Both radicals and rational exponents are used to simplify expressions and solve equations.

Once the basics have been covered, it is important to have a method for tackling the worksheet. Begin by breaking the problem into parts and identifying the radicals and rational exponents. This can be done by looking for the symbol √ or ^. Once the radicals and rational exponents have been identified, it is important to simplify the expression as much as possible. This can be done by using the laws of exponents, such as a^m x a^n = a^m+n and a^m/a^n = a^m-n.

[toc]

After simplifying the expression, it is important to check the answer to make sure it is correct. This can be done by substituting the answer back into the original problem and seeing if the equation is true. If it is not, it is important to go back and identify any mistakes that have been made.

By following these steps and understanding the basics, tackling radicals and rational exponents on a worksheet can be a matter of ease. With any difficult equation, the key is to take it step by step and understand the concept before diving into the numbers.

Understanding Radicals and Rational Exponents: Tips and Tricks for Working Through the Worksheet

Radicals and rational exponents are important topics for students to understand. Knowing how to work through a worksheet can help a student master these concepts. Here are some tips and tricks for working through a worksheet on radicals and rational exponents to help ensure success.

First, it is important to understand the basic rules of radicals and rational exponents. These include being able to simplify radicals, apply the power rule for rational exponents, and use the product and quotient rules for rational exponents. Knowing the rules and how they work will make it much easier to complete the worksheet.

Second, it is important to take some time to understand the problem before beginning to solve it. Read through the problem carefully and think about what it is asking. It is also helpful to draw a diagram or sketch to help visualize the problem.

Third, it is important to use the correct notation when working through a worksheet. For example, when writing out radical expressions, use the square root symbol and make sure to include the radical sign. Also, when working with rational exponents, it is important to use parentheses to indicate the base and the exponent.

Finally, it is important to be organized when working through a worksheet. For example, it is helpful to keep the radical expression and the rational exponent on separate lines. This makes it easier to see the structure of the problem and how the different components are related.

By following these tips and tricks, working through a worksheet on radicals and rational exponents can be much easier. Understanding the basic rules, taking the time to understand the problem, using the correct notation, and staying organized are all key to mastering these concepts.

Radical and Rational Exponents: A Comprehensive Guide to Working Through the Worksheet

Radical and rational exponents are two types of exponents commonly encountered in mathematics. A radical exponent is an exponent that contains a root of a number, while a rational exponent is an exponent that contains an integer or fraction. Both types of exponents can be intimidating to tackle, but with a few key tips and tricks, they can be easily navigated.

When working with radical and rational exponents, it is important to understand the rules and properties of exponents. It is also essential to be able to identify the difference between a radical exponent and a rational exponent. A radical exponent is written as a root sign, typically with a number inside the root sign, such as square root of two. A rational exponent is written with a base number, followed by an integer or fractional exponent, such as x^2/3.

When working through a worksheet involving radical and rational exponents, it is important to begin by identifying the type of exponent being worked with. Once the type of exponent is identified, it is important to understand the rules and properties associated with that type of exponent. For example, when working with radical exponents, it is important to remember that the root of a number can be simplified by finding square roots, cube roots, and so on. When working with rational exponents, it is important to remember that the base number can be raised to a power, and that fractional exponents can be simplified by finding the reciprocal of the fractional exponent and then raising the base number to that power.

When working with radical exponents, it is also important to remember that a number raised to a radical exponent can be simplified by finding the root of the number, and then raising the simplified number to the same exponent. For example, if a worksheet contains the expression 3^(2/3), then it can be simplified by finding the cube root of 3, which is 1.44, and then raising 1.44 to the same exponent, which is 1.44^(2/3).

When working with rational exponents, it is important to remember that exponents can be added, subtracted, multiplied, and divided. For example, if a worksheet contains the expression x^2/3 * x^-1/2, then it can be simplified by adding the exponents to get x^(5/6).

Finally, when working with radical and rational exponents, it is important to remember that the rules and properties of exponents apply to all types of exponents. For example, a worksheet may contain the expression (x^2/3)^-1/2. This expression can be simplified by first taking the reciprocal of the power and then raising the base number to that power, which is x^(-3/2).

By understanding the rules and properties of radical and rational exponents, and by being able to identify the type of exponent being worked with, it is possible to successfully navigate a worksheet involving radical and rational exponents. With patience and practice, anyone can become an expert at working through such a worksheet.

Conclusion

The Radicals and Rational Exponents Worksheet is a great tool to help students better understand how to work with radicals and rational exponents. It can help students practice the concepts they need to know in order to solve equations and simplify expressions with radicals and rational exponents. With practice, students can become more confident in their ability to manipulate radicals and rational exponents.

[addtoany]