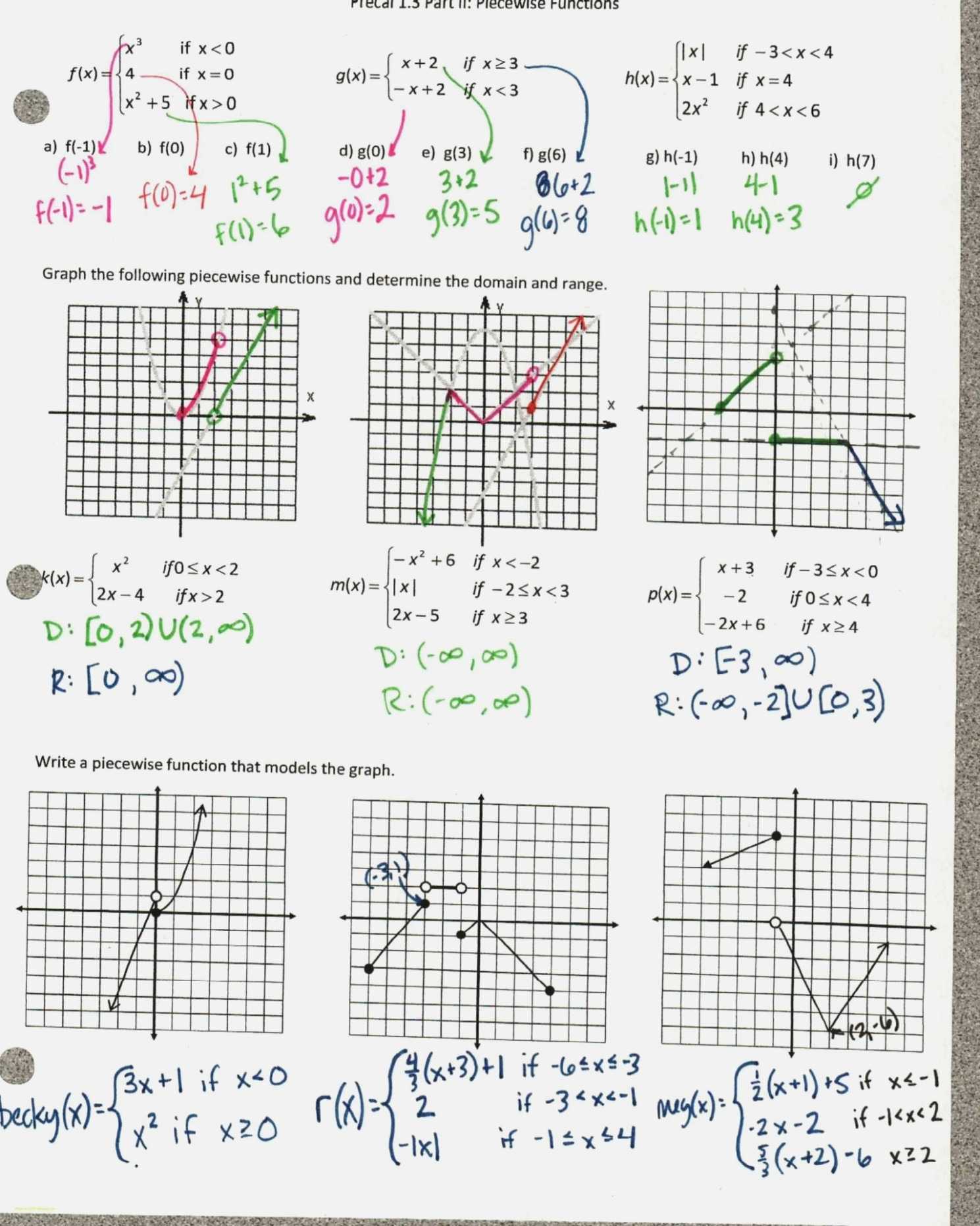
Exploring Quadratic Functions: A Step-by-Step Guide to Solving Quadratic Equations with a Worksheet and Answers
Introduction
Quadratic functions are ubiquitous in mathematics. They are used to model many different phenomena, from the motion of a projectile to the path of a wave. They are also used to solve problems in many fields, including engineering, physics, and economics. Despite their ubiquity, quadratic functions can be difficult to understand and master. This guide provides a step-by-step approach to solving quadratic equations with a worksheet and answers.
Overview of Quadratic Functions
[toc]
A quadratic function is an equation of the form ax2 + bx + c = 0, where a, b, and c are constants. The most common type of quadratic equation is the standard form, in which a is not equal to zero. The standard form of a quadratic equation can be written as ax2 + bx + c = 0, where a, b, and c are constants. The solution to a quadratic equation is the set of values that make the equation true.
Solving Quadratic Equations
There are several methods for solving quadratic equations. The most commonly used method is factoring. Factoring involves breaking down an equation into two or more simpler equations. This can be done by multiplying the terms together and using the distributive property.
For example, consider the equation x2 + 5x + 6 = 0. This equation can be factored into the product (x + 3)(x + 2) = 0. The solutions to the equation can then be found by setting each factor equal to zero and solving for x. In this case, the solutions are x = -3 and x = -2.
Another method for solving quadratic equations is the quadratic formula. The quadratic formula is an equation that can be used to find the solutions of any quadratic equation. The formula is: x = [-b ± √(b2 – 4ac)] / 2a.
Using the Worksheet
The worksheet provided in the guide contains several examples of quadratic equations and their solutions. To use the worksheet, read each equation and determine which method should be used to solve it. If the equation can be factored, use the factoring method. If the equation cannot be factored, use the quadratic formula.
Once the method has been determined, solve the equation using the appropriate method. Finally, check your answer by plugging it back into the original equation and verifying that it is correct.
Conclusion
This guide provides a step-by-step approach to solving quadratic equations with a worksheet and answers. Understanding and mastering quadratic functions can be difficult, but with practice and dedication, it can be done. The worksheet provided in the guide is a great starting point for mastering quadratic equations.
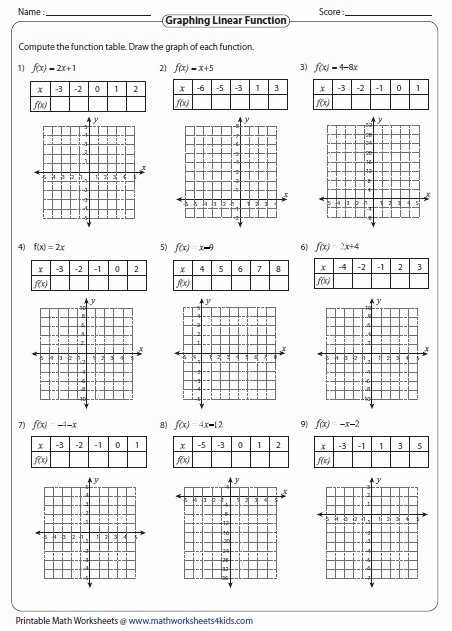
Making Sense of Graphs: How to Visualize Quadratic Functions with a Worksheet and Answers
Visualizing quadratic functions can be a challenging task for students. A worksheet with answers is one way to help them become more familiar with them. This worksheet will guide students through the process of graphing a quadratic function.
First, students will need to define the variables in the equation. They should identify the coefficients of the equation and the constant. This will help them determine the graph’s shape.
Next, students will need to rewrite the equation in standard form. To do this, they should move the constant to the right side of the equation and set the equation equal to zero.
Once the equation is in standard form, students can use a table of values to graph the function. They should begin by creating a table with two columns, one for x and one for y. Then, they should plug in different values for x and calculate the corresponding y-values. This will help them create a graph of the equation.
Finally, students should use the graph to determine the equation’s x- and y-intercepts. Once they have these values, they can determine the vertex of the graph. The vertex is the point at which the graph changes direction.
By following these steps, students will be able to visualize quadratic functions and understand how changing the equation’s coefficients can affect the graph’s shape. A worksheet and answers can provide them with the guidance and practice they need to understand this concept.
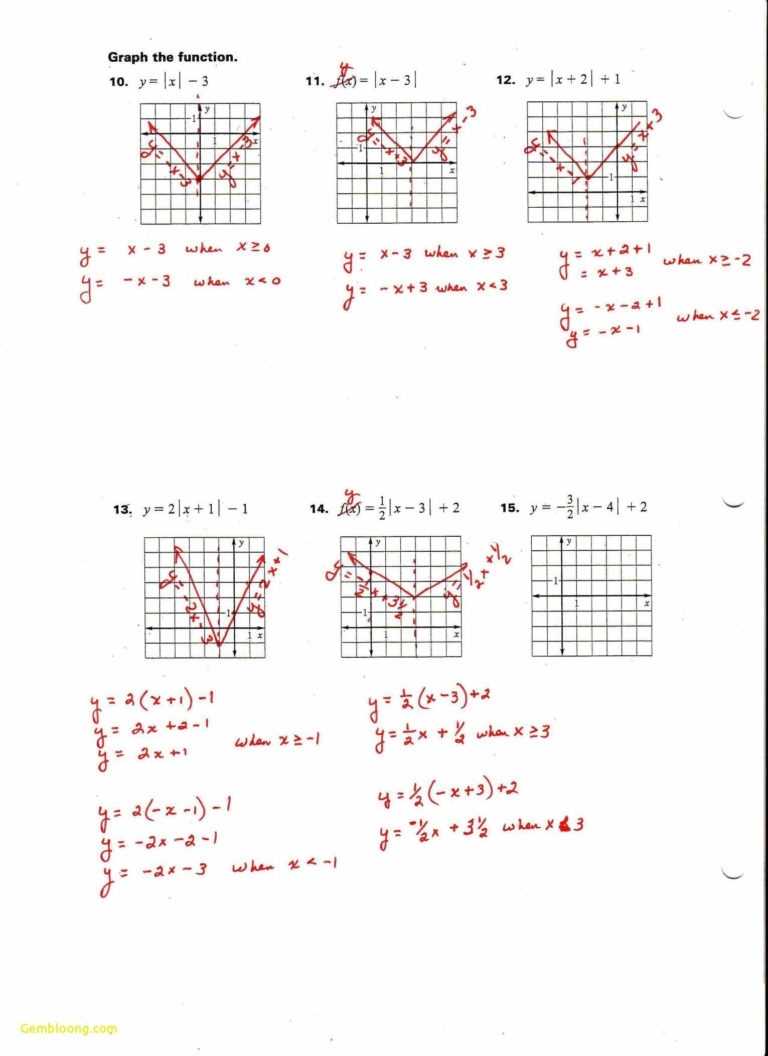
Simplifying Solutions: An Introduction to Factoring Quadratic Equations with a Worksheet and Answers
This worksheet introduces students to the concept of factoring quadratic equations. It is designed to help them gain an understanding of the basics of factoring and how to use the process to simplify solutions.
The worksheet begins with a description of the process of factoring, including examples of how it can be used to find solutions for quadratic equations. This is followed by a set of practice problems with solutions. The practice problems are designed to give students an opportunity to apply what they have learned about factoring quadratic equations.
At the end of the worksheet, there is a section of answers to the practice problems. These answers will help students check their work and gauge their understanding of the material.
This worksheet is an ideal starting point for students who are learning how to factor quadratic equations. It is an accessible introduction to the concept and provides a thorough explanation of the process. By working through the practice problems, students will gain a better understanding of how to factor quadratic equations and use them to simplify solutions.
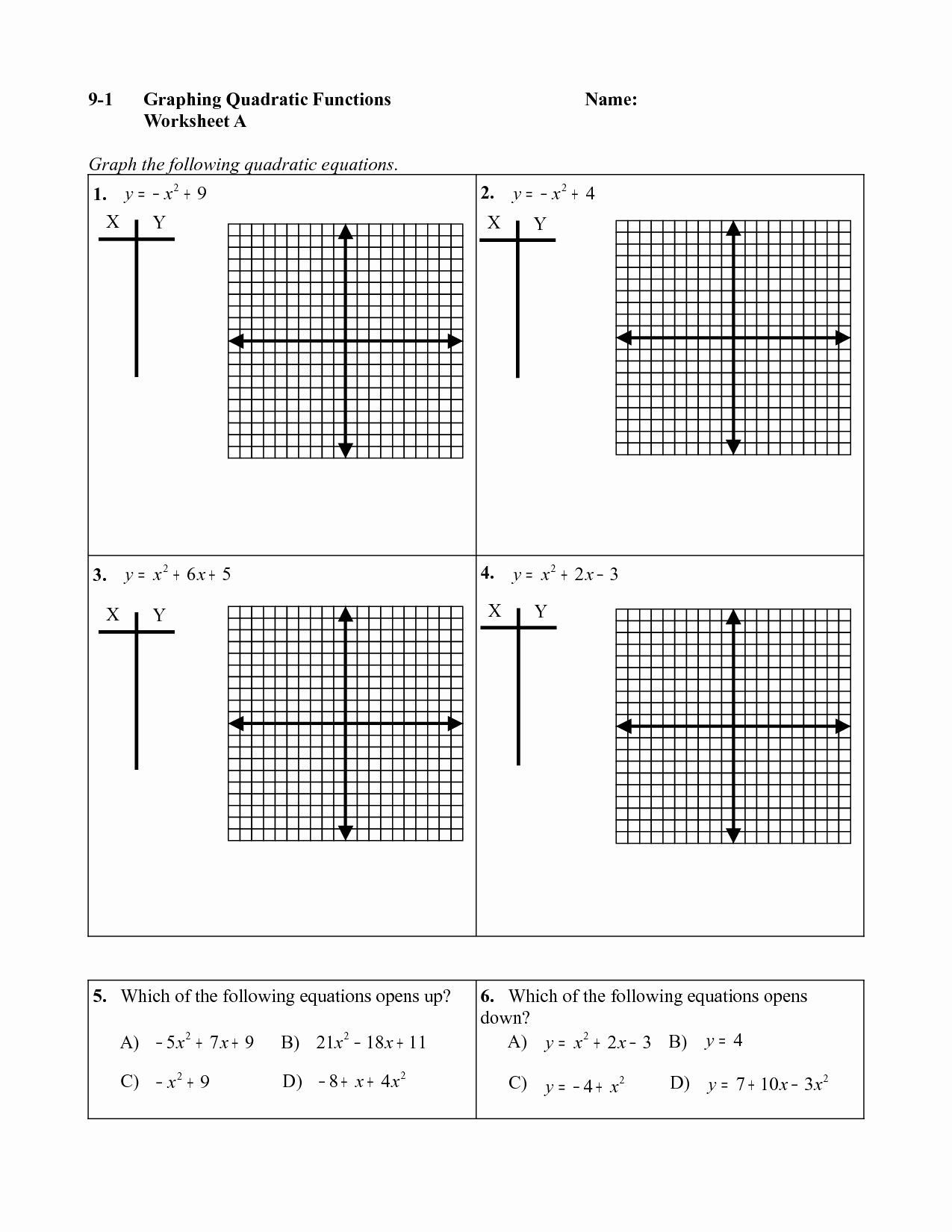
Extending Knowledge: Gaining a Deeper Understanding of Quadratic Functions with a Worksheet and Answers
Quadratic functions are a type of nonlinear equation defined by an equation of the form y = ax² + bx + c, where a, b, and c are real numbers. They can be used to model a wide range of phenomena, from simple projectile motion to complex economic trends. Understanding the properties of quadratic functions is essential for those studying mathematics and other related fields.
This worksheet is designed to help learners gain a deeper understanding of quadratic functions. The worksheet begins with a basic introduction to the subject, followed by some practice problems. Answers are provided so learners can check their work.
Part 1: Introduction to Quadratic Functions
1. What is a quadratic function?
A quadratic function is an equation of the form y = ax² + bx + c, where a, b, and c are real numbers. It is a type of nonlinear equation.
2. What are the parts of a quadratic function?
The parts of a quadratic function are the coefficients a, b, and c, and the variables x and y.
3. What are the characteristics of a quadratic function?
A quadratic function has a minimum or maximum point, which is called the vertex. It also has an axis of symmetry which is the line that divides the graph of the function in half. The graph of a quadratic function is called a parabola.
4. What are some real-world applications of quadratic functions?
Quadratic functions can be used to model a wide range of phenomena, from simple projectile motion to complex economic trends. They can also be used to calculate the maximum height of an object thrown into the air, or the time it takes for an object to reach the ground.
Part 2: Practice Problems
1. Graph the quadratic function y = 2x² + 3x + 5.
The graph of this function is a parabola that opens upward, with its vertex at (1, 8). The line of symmetry is x = -1.5.
2. Find the vertex and line of symmetry for the quadratic function y = -3x² + 5x – 4.
The vertex of this quadratic function is (2.5, -9.5), and its line of symmetry is x = 2.5.
3. Find the roots of the quadratic function y = 4x² + 6x – 5.
The roots of this quadratic function are x = -1.5 and x = 0.5.
4. Find the y-intercept of the quadratic function y = -2x² + 3x – 5.
The y-intercept of this quadratic function is -5.
Conclusion
This quadratic functions worksheet with answers provides an excellent opportunity to practice and review the concepts of quadratic equations. By completing the worksheet, students will have a better understanding of how to solve quadratic equations and be able to apply that knowledge in other areas. This worksheet is a valuable resource for students who are preparing for exams or looking to increase their basic math skills.
[addtoany]