Exploring the Fundamentals of Probability of Compound Events: An In-Depth Analysis of Worksheets and Examples

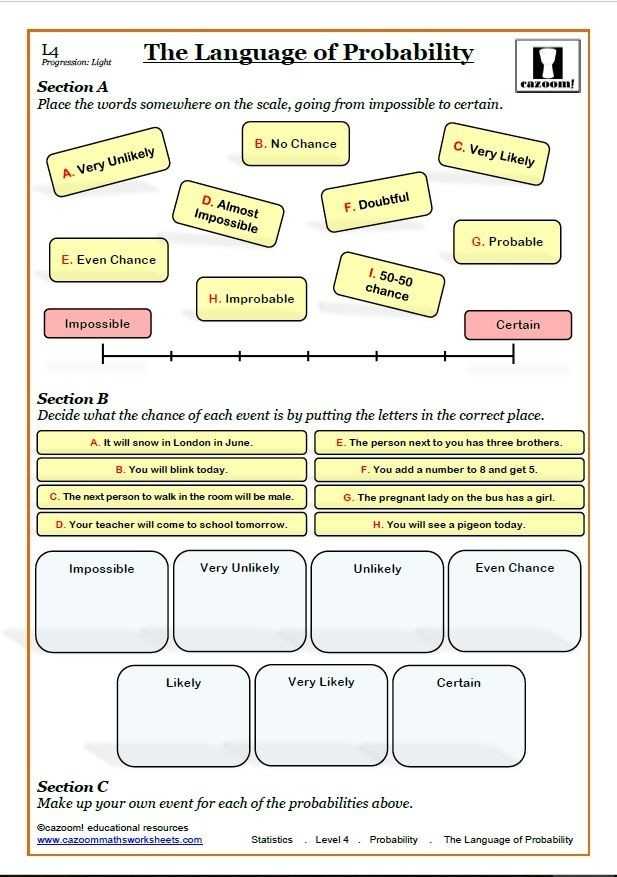
The field of probability is a vital component of mathematics, and its study is of great importance for understanding the fundamental principles of randomness and chance. Compound events are a particular type of probability in which multiple events are involved, and the occurrences of each event must be considered in order to accurately calculate the likelihood of the event as a whole. This article will explore the fundamentals of probability of compound events through an in-depth analysis of worksheets and examples.

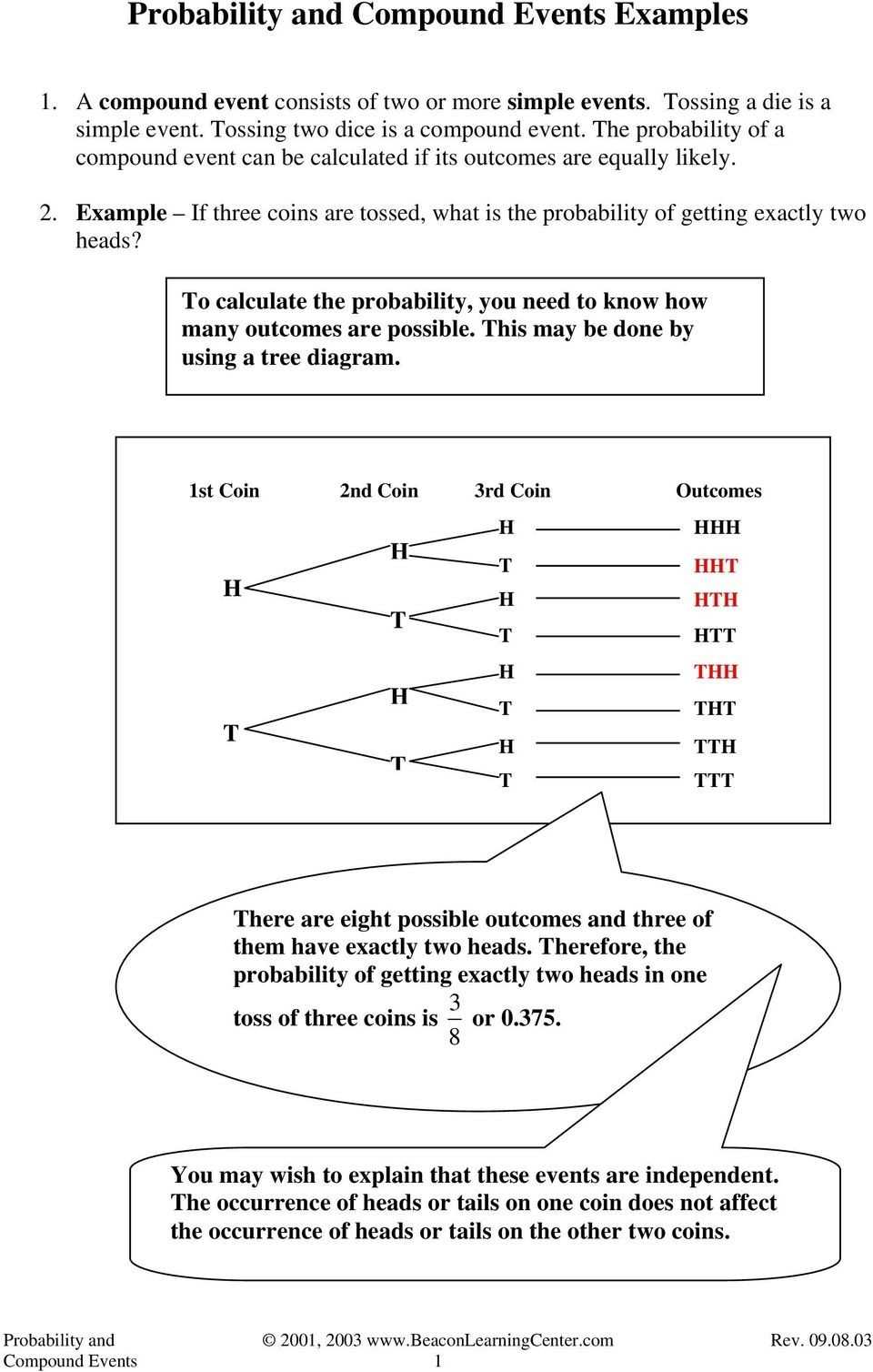
The first step in understanding the fundamentals of probability of compound events is to become familiar with the terminology. A “compound event” is an event that is composed of two or more events, or “simple events,” that are related to each other. For example, if a coin is flipped and a die is rolled, the simple events would be the coin toss and the roll of the die, and the compound event would be the result of both of these events combined. The probability of any compound event is the product of the probabilities of the individual events.

Once a basic understanding of the terminology has been established, it is important to understand the concept of conditional probability. Conditional probability is the probability of an event occurring given that one or more other events have already occurred. For example, if a coin is flipped and the result is heads, then the probability of rolling a 6 on a die is different than if the coin had been flipped and landed on tails.

To further understand the fundamentals of probability of compound events, it is important to become familiar with the different types of probability worksheets and examples. Worksheets are useful tools for gaining an understanding of the probability of compound events. They typically involve a series of simple events, such as flipping a coin or rolling a die, and then require students to calculate the probability of a resulting compound event, such as the result of flipping a coin and then rolling a die.

Examples are also an invaluable tool for understanding the fundamentals of probability of compound events. Examples can help to illustrate the concepts of simple and compound events, as well as conditional probability. Examples can also provide a visual representation of the probability of various compound events, which can be helpful for understanding how the probabilities of individual events can affect the probability of a compound event.

In conclusion, the fundamentals of probability of compound events can be understood through an in-depth analysis of worksheets and examples. Through a better understanding of the terminology and concepts involved, students can gain an understanding of the probability of various compound events and how the probabilities of individual events can affect the probability of a compound event.

Probability of Compound Events: A Comprehensive Guide to Analyzing Probability Using Worksheets

Probability of compound events is an important concept to understand when analyzing chances and outcomes of different scenarios. In this comprehensive guide, we will discuss the basics of probability, how to calculate it, and how to create worksheets for analyzing it.

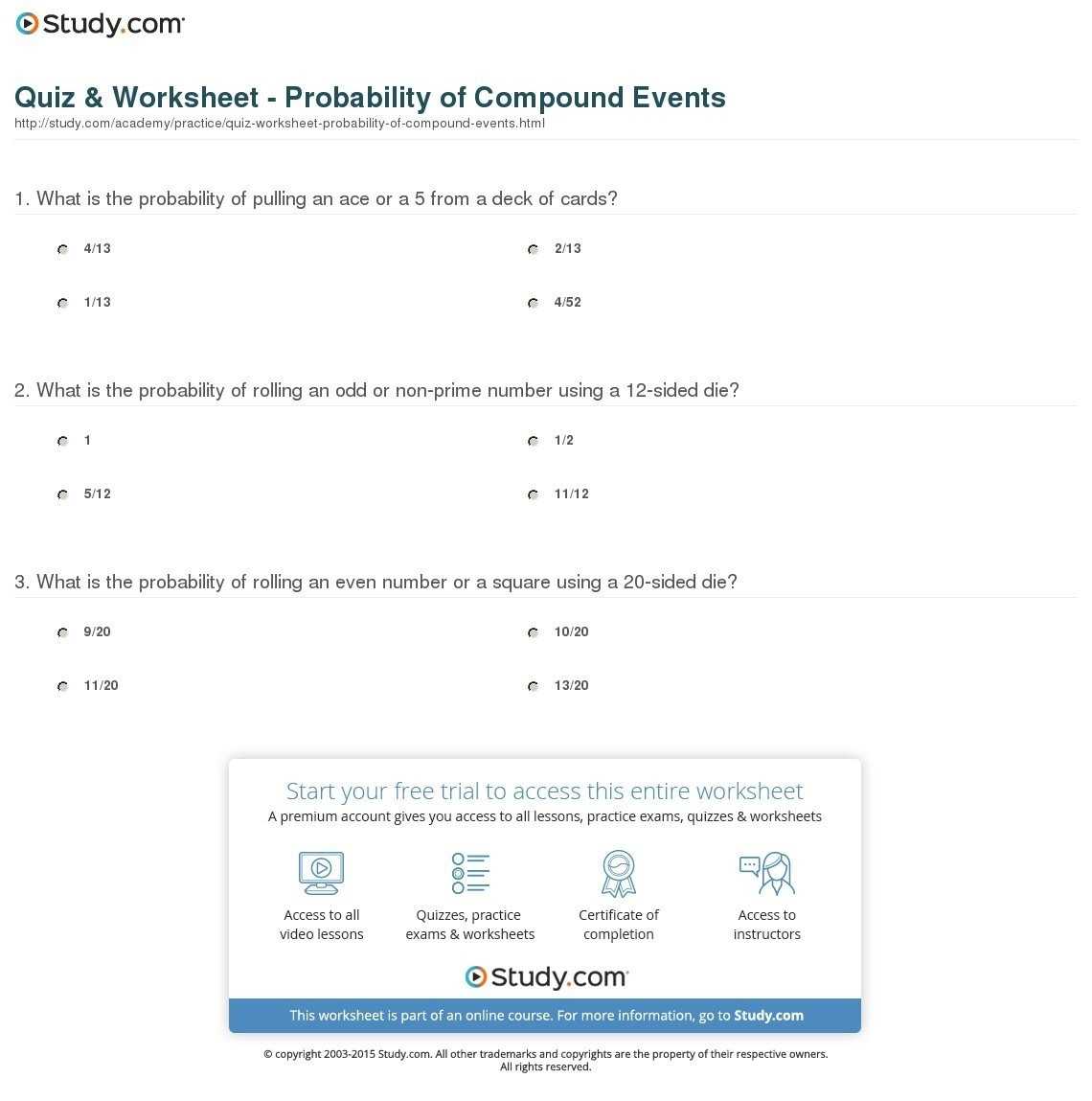
Probability is a measure of the likelihood that an event will occur. It is expressed as a fraction, decimal, or percentage. A probability of one indicates certainty, while a probability of zero indicates impossibility. To calculate the probability of a compound event, you must consider the probability of each event in the sequence occurring.

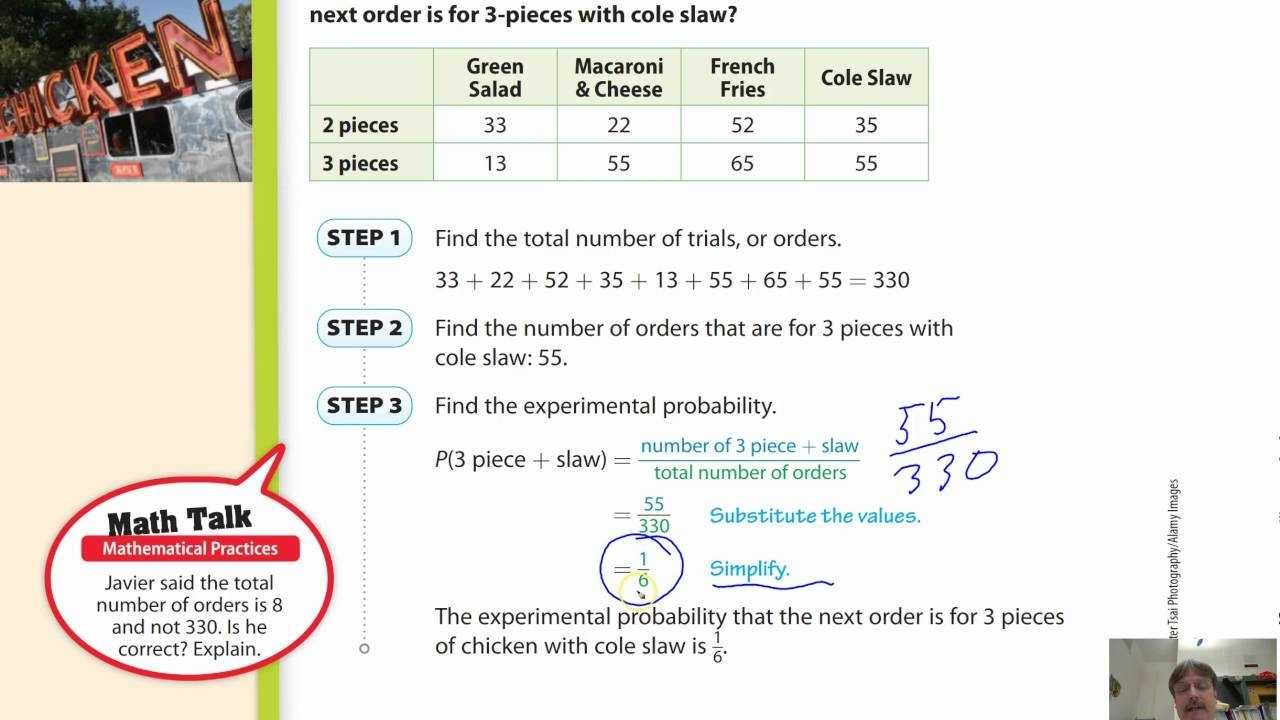
The first step in analyzing probability is to identify all the possible outcomes of the events. This can be done by creating a list of the possible outcomes for each event in the sequence. For example, if you were analyzing the probability of rolling a six on a dice, you would list all the possible outcomes as 1, 2, 3, 4, 5, and 6.

Once you have identified all the possible outcomes of the events, you can calculate the probability of each outcome. To do this, you will need to use a formula. The formula for calculating the probability of a single event is the number of possible outcomes divided by the total number of outcomes. For example, if you were analyzing the probability of rolling a six on a dice, you would divide 6 (the total number of outcomes) by 6 (the number of possible outcomes) to get a probability of 1.

To calculate the probability of a compound event, you will need to use a different formula. This formula is the product of all the individual probabilities of each event in the sequence. For example, if you were analyzing the probability of rolling two sixes on a pair of dice, you would multiply 1 (the probability of rolling a six on the first dice) by 1 (the probability of rolling a six on the second dice) to get a probability of 1.

Once you have calculated the probabilities of the events, you can create a worksheet to analyze the probability of the compound event. To do this, you will need to create a table with the probability of each event in the sequence listed in the left-hand column. Then, calculate the probability of the compound event by multiplying all the probabilities together.

This guide has provided an overview of how to analyze probability using worksheets. By following these steps, you can easily calculate the probability of a compound event and create a worksheet to analyze the data. With this knowledge, you can better understand the chances and outcomes of various scenarios.

Leveraging Probability of Compound Events Worksheets to Develop Stronger Math Skills: An Overview of the Benefits

Probability of compound events worksheets have become increasingly popular among math educators in recent years. These worksheets are designed to help students develop an understanding of the principles of probability, as well as to expand their knowledge of mathematics in general. By introducing students to these worksheets, educators can help students develop their math skills, build an understanding of probability, and gain a better understanding of how to apply probability to everyday life.

Probability of compound events worksheets allow students to practice the application of probability principles. These worksheets offer students practice in solving problems that involve multiple events, such as the probability of a certain outcome occurring if two or more events occur simultaneously. This type of problem-solving is invaluable for students as it helps them to develop the ability to think logically and make informed decisions. By working through the worksheets, students can practice the application of probability principles and gain a better understanding of how to apply probability to their own life.

The use of probability of compound events worksheets also allows students to gain a better understanding of basic mathematics concepts. By using these worksheets, students can gain a better understanding of the principles behind addition, subtraction, multiplication, division, and other basic operations. As a result, students can develop a better understanding of how to apply these concepts in their own lives, as well as gain a better understanding of the logic behind probability.

Finally, using probability of compound events worksheets can help students build a better understanding of probability and its application in everyday life. By working through these worksheets, students can learn how to apply probability to the events they encounter in their everyday lives. For example, students can learn how to calculate the probability of a certain event occurring if two or more events occur simultaneously. This type of understanding can help students make informed decisions about the future and how to best manage their own lives.

Overall, probability of compound events worksheets can benefit students in a variety of ways. By practicing the application of probability principles, students can gain an understanding of how to apply probability to their own lives. Additionally, students can build an understanding of basic mathematics concepts and gain a better understanding of the logic behind probability. Finally, these worksheets can help students develop a better understanding of probability and its application in everyday life.

Conclusion

The Probability of Compound Events Worksheet is a great resource for teaching students about the concept of probability and the importance of understanding the different types of probability. It provides a comprehensive overview of the different types of probability and helps students understand the different ways that probability can be used. By understanding the different types of probability and their uses, students can gain a better understanding of the world around them and the probability of various events.