Exploring the Benefits of Using Piecewise Functions Worksheet Answer Key

Piecewise functions are a powerful mathematical tool that can be used to model a variety of physical phenomena. They provide an efficient way to express a function in terms of a set of simpler functions, each of which is valid in a certain region of the domain. This allows for a more intuitive understanding of the behavior of the function, and can aid in its interpretation and solution.

The primary benefit of using piecewise functions is that they can be constructed to model complex behaviors that would not be possible with a single function. For instance, a piecewise function can be used to describe a system which behaves differently in different regions. This is useful in situations where a single function might not accurately capture the behavior. Additionally, piecewise functions can be used to represent mathematical objects that have discontinuous behavior.

The use of piecewise functions also enables the practice of breaking a problem down into smaller parts, thereby making it more manageable. By expressing a problem in terms of several simpler functions, it becomes easier to identify the relationships between different parts of the problem. Moreover, the use of piecewise functions can facilitate the development of numerical methods for solving a problem, as the behavior of the function can be better analyzed and understood.

Overall, piecewise functions are a very powerful mathematical tool which can be used to model a variety of physical phenomena. They provide an efficient way to express a function in terms of several simpler functions, each of which is valid in a certain region of the domain. This allows for a more intuitive understanding of the behavior of the function, and can aid in its interpretation and solution. Furthermore, they enable the breaking down of a problem into smaller parts, thus making it more manageable. All of these benefits make the use of piecewise functions an invaluable tool in the practice of mathematics.

Understanding Piecewise Functions and Their Graphs: A Step by Step Guide

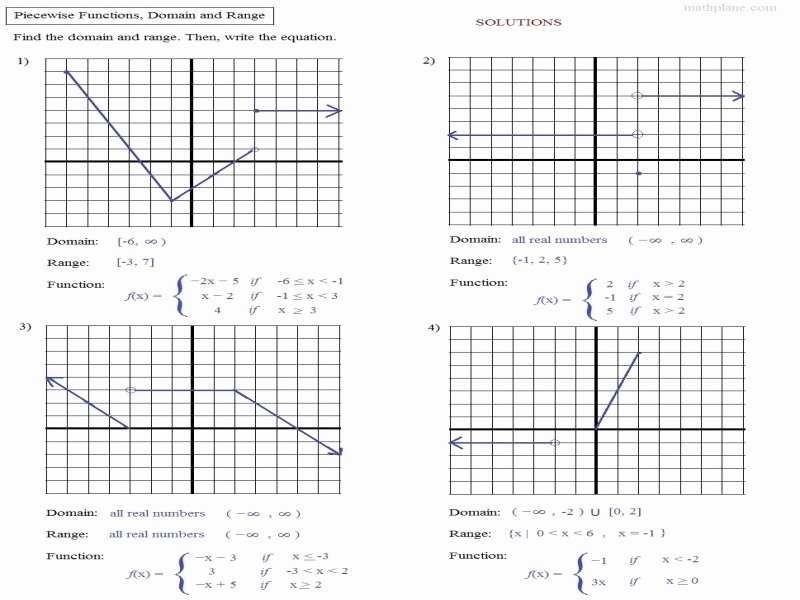
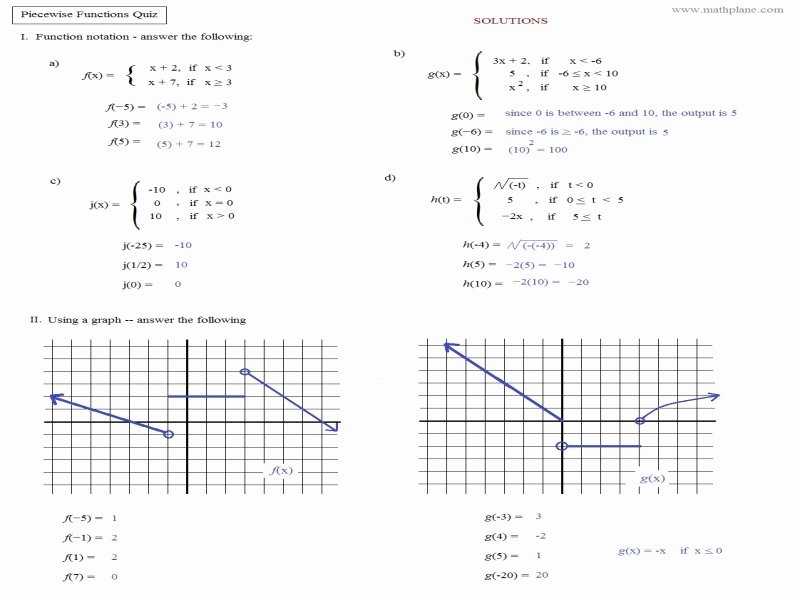
Piecewise functions are an important mathematical tool used to define mathematical relationships between two variables. In a piecewise function, the domain of the function is divided into a number of distinct intervals, and a different function is specified for each of the intervals. This type of function can be used to model a variety of real-world scenarios, such as setting different prices for different quantities of a product.

The graph of a piecewise function consists of multiple distinct pieces, each of which corresponds to a different interval of the domain. To understand how to graph a piecewise function, it is essential to first understand what the function looks like.

To begin, let’s consider a simple example of a piecewise function. Suppose we have the following piecewise function:

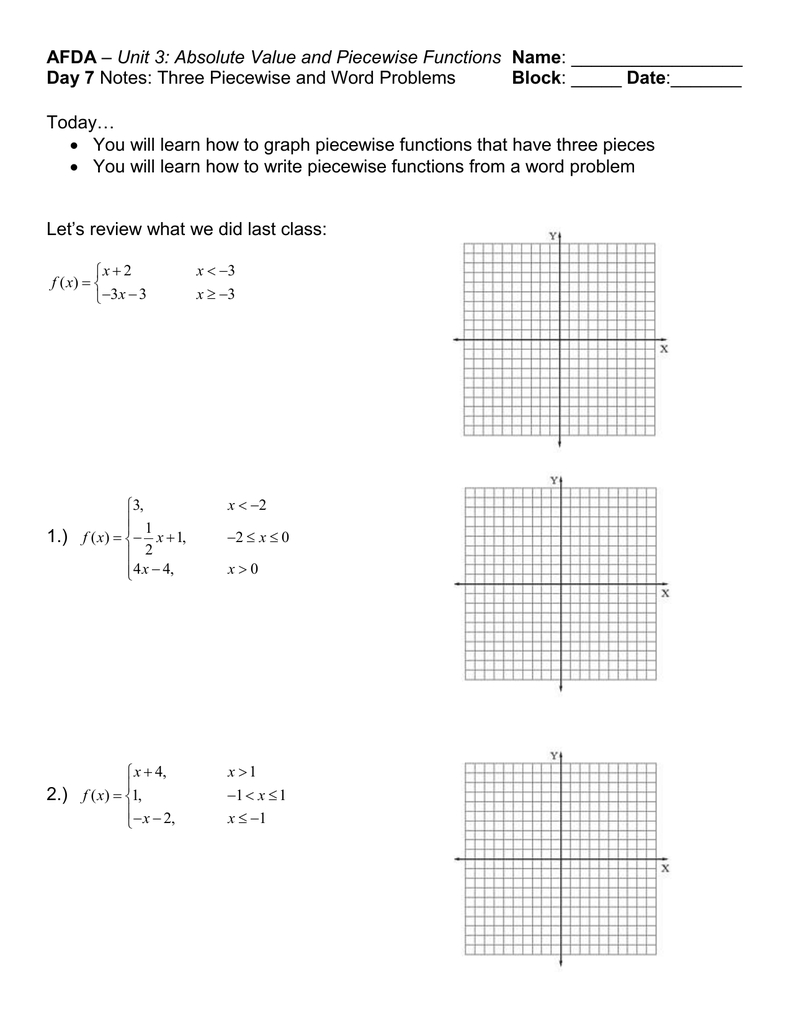
f(x) = {x^2 if x < 0, x if 0 ≤ x < 1, 2x if 1 ≤ x ≤ 2} This function is defined by three different pieces, each of which is valid for a different range of the domain. The first piece is defined for values of x less than 0, the second piece is defined for values of x between 0 and 1, and the third piece is defined for values of x between 1 and 2. Now that we know what the function looks like, we can begin to graph it. To do this, we need to start by plotting the points that define each piece of the function. For this example, the points that define the first piece of the function are (-1,1), (-2,4), and (-3,9). These points can be plotted on a graph, and then the rest of the points of the first piece can be connected with a straight line. The same process can be repeated for the other pieces of the function. For the second piece of the function, the points that must be plotted are (0,0), (1,1) and (2,2). For the third piece, the points that must be plotted are (1,2), (2,4) and (3,6). Once all of the points have been plotted, the graph of the piecewise function can be drawn by connecting all of the points with straight lines. Graphing piecewise functions can be a bit tricky, but with some practice and a bit of patience, it is possible to understand how to do it. Once a person understands the basics of graphing piecewise functions, they can start using them to model a variety of real-world scenarios.

Comparing Different Types of Piecewise Functions and Their Uses

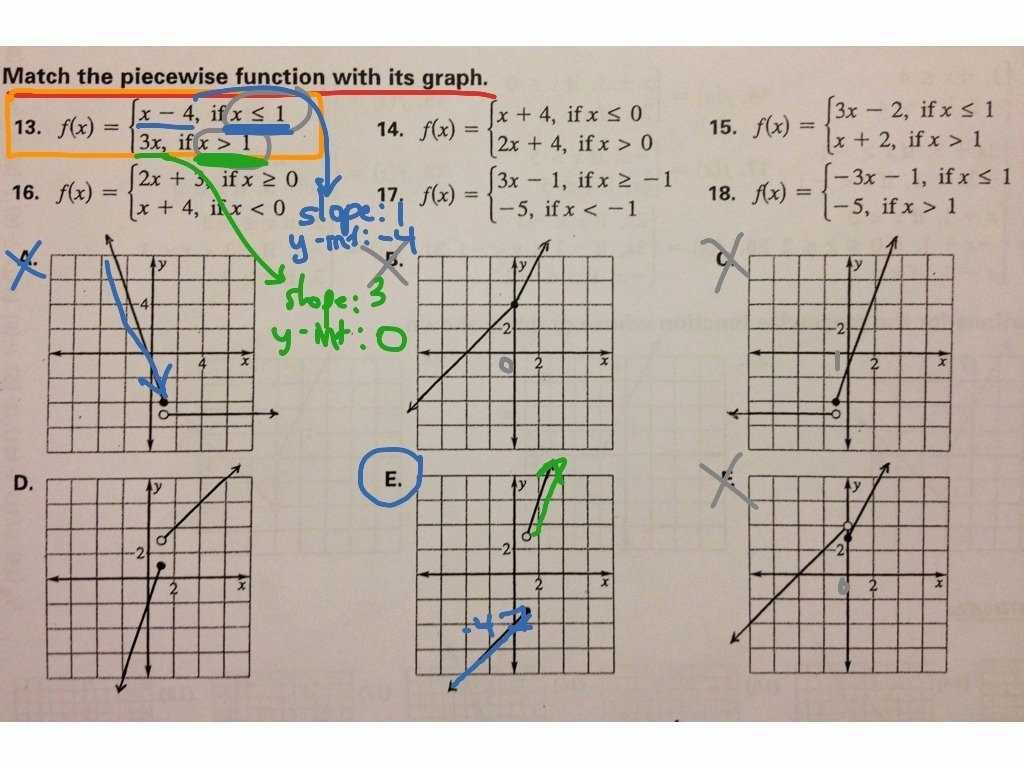
Piecewise functions are mathematical expressions composed of two or more distinct equations, or “pieces,” connected by a vertical line on a graph. These functions are useful when applied to a variety of scenarios, such as the analysis of data, graphing the motion of an object, or the evaluation of certain types of equations. Depending on the purpose, different types of piecewise functions can be used.

One type of piecewise function is the step function. This type of function uses a series of vertical lines, or steps, to represent discontinuous values. Step functions are useful for modeling decisions with binary, or two-valued, outcomes. For example, a step function could be used to graph a scenario where a person earns a certain amount for each hour worked up to 40 hours, then earns double the amount for each hour worked over 40.

Another type of piecewise function is the absolute value function. This function is composed of two straight line segments connected by a corner point at the origin. The absolute value function is useful in cases where the value of a number must remain positive, no matter how large or small the number is. For example, the absolute value function could be used to evaluate a scenario where the distance a person travels must remain positive, regardless of whether the distance is in the positive or negative direction.

Finally, the piecewise linear function is composed of multiple linear line segments connected at the points where they intersect. This type of function is useful for modeling situations where the rate of change of a variable is not constant. For example, a piecewise linear function could be used to graph a situation where the price of a product changes depending on the quantity purchased.

In conclusion, piecewise functions have a variety of uses in mathematics, and the type of function used depends on the scenario being modeled. Step functions are useful for representing binary outcomes, absolute value functions are useful for representing numbers that must remain positive, and piecewise linear functions are useful for representing situations where the rate of change of a variable is not constant.

How to Solve Real-World Problems Using Piecewise Functions Worksheet Answer Key

1. Problem: You are on a budget and want to save money on groceries.

Solution: Create a piecewise function that represents your budget. Your budget can be broken up into two parts: one for groceries and one for other items. For the “groceries” section, you can set a limit for how much you can spend each week. This limit can be represented as a piecewise function. You can set a maximum for how much you can spend on groceries each week, and if you go over that, you will have to pay a penalty. This could be represented as a piecewise function in the following way:

f(x) =
{ 0, x < grocery budget limit { penalty amount, x ≥ grocery budget limit For the “other items” section, you can set a limit for how much you can spend. This could be represented as a piecewise function in the following way: g(x) = { 0, x < other items budget limit { penalty amount, x ≥ other items budget limit By using piecewise functions to represent your budget, you can easily track your spending and ensure that you don’t exceed your budget. 2. Problem: You want to save for a vacation but are unsure how much you should save each month. Solution: Create a piecewise function that represents your savings plan. Your savings plan can be broken up into two parts: one for the amount you need to save each month and one for the amount you need to save each year. For the “monthly” section, you can set a limit for how much you should save each month, and if you go over that, you will have to pay a penalty. This could be represented as a piecewise function in the following way: h(x) = { 0, x < monthly savings limit { penalty amount, x ≥ monthly savings limit For the “yearly” section, you can set a limit for how much you should save each year and if you go over that, you will have to pay a penalty. This could be represented as a piecewise function in the following way: i(x) = { 0, x < yearly savings limit { penalty amount, x ≥ yearly savings limit By using piecewise functions to represent your savings plan, you can easily track your progress and ensure that you save enough money for your vacation.

Conclusion

The Piecewise Functions Worksheet Answer Key provided a comprehensive overview of the fundamentals of piecewise functions. By working through the worksheet, students were able to gain a better understanding of the various types of functions, how to graph them, and how to solve them. With a better understanding of the material, students can now use this knowledge to solve real-world problems.