How to Use Scientific Notation to Streamline Operations in a Worksheet

Scientific notation is a compact way of expressing very large or very small numbers. It streamlines operations in a worksheet, reducing the amount of time needed to perform certain calculations, and can be beneficial in situations where a large number of calculations are involved.

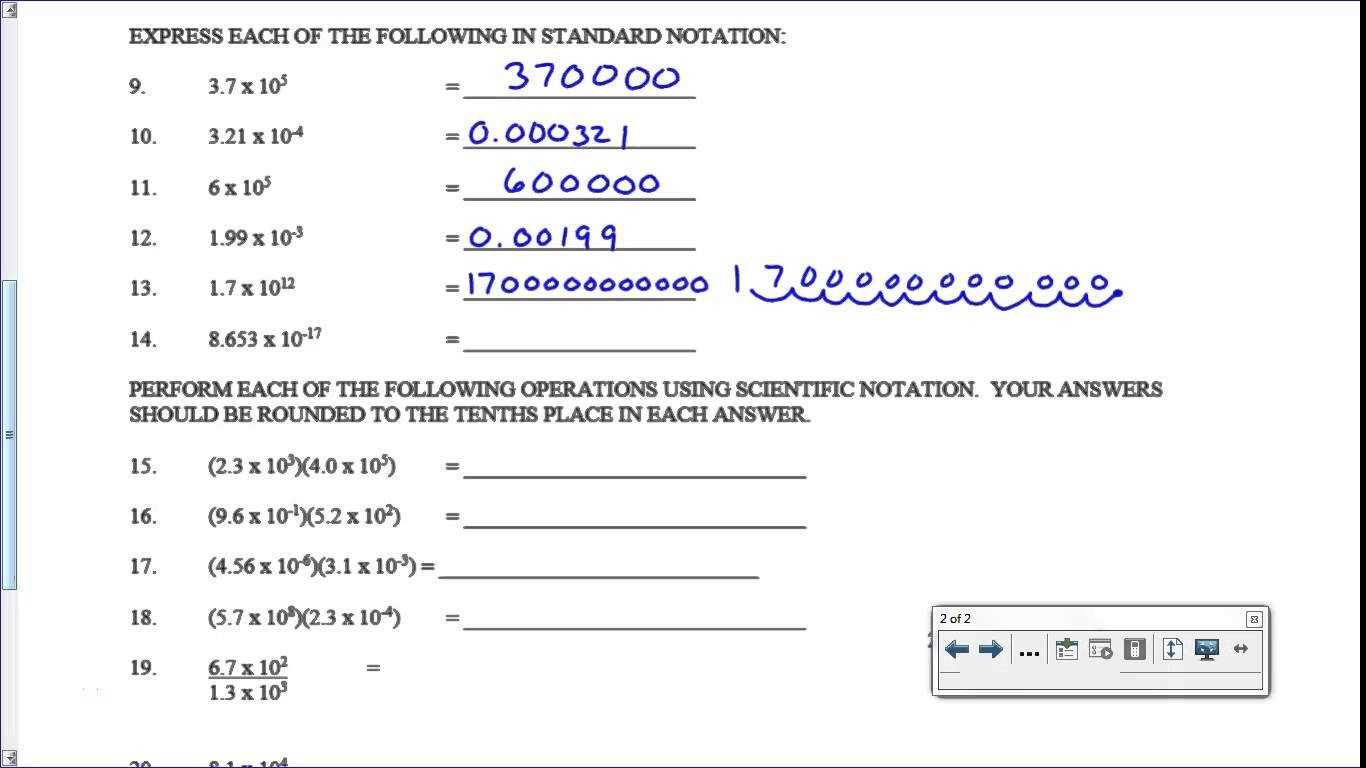
To use scientific notation in a worksheet, the number must be written in the form of a coefficient multiplied by a power of 10. For example, the number 1000 can be written as 1×10³. To calculate the value of a number written in scientific notation, the coefficient must be multiplied by 10 to the power of the exponent.

When performing calculations, scientific notation can simplify the process. When adding or subtracting two numbers written in scientific notation, the coefficients must be added or subtracted, while the exponents must remain the same. For example, when adding 1×10³ and 5×10³, the result is 6×10³.

[toc]

When multiplying two numbers written in scientific notation, the coefficients must be multiplied while the exponents must be added. For example, when multiplying 1×10⁴ and 5×10³, the result is 5×10⁷.

When dividing two numbers written in scientific notation, the coefficients must be divided and the exponents must be subtracted. For example, when dividing 5×10⁷ and 2×10³, the result is 2.5×10⁴.

Using scientific notation in a worksheet can help to reduce the number of calculations needed, as well as ensuring accuracy when dealing with very large or very small numbers. When used properly, it can greatly streamline operations and save time.

Exploring the Benefits of Scientific Notation for Operations on a Worksheet

Scientific notation is a useful tool for quickly performing calculations on a worksheet. The notation is especially beneficial when calculations involve large or small numbers, as it allows for quick and accurate operations.

In scientific notation, a number is written in the form of a coefficient multiplied by a power of 10. For example, 1000 can be written as 1 x 103. This simplifies working with numbers that have large or small values.

When performing calculations with large or small numbers, scientific notation is beneficial because it reduces the number of decimal places used. This makes calculations easier and less prone to errors. Additionally, numbers in scientific notation can be more easily compared and contrasted.

Scientific notation also makes it easier to interpret and visualize the size of a number. For example, a number written in scientific notation is easier to interpret than a number with a large number of decimal places.

Finally, scientific notation is beneficial for operations involving addition and subtraction. When two numbers in scientific notation are added or subtracted, the coefficients and exponents can be combined to form a single number. This simplifies calculations and reduces the risk of mistakes.

Overall, scientific notation is a useful tool for quickly and accurately performing operations on a worksheet. It simplifies calculations involving large or small numbers, and makes it easier to interpret and visualize the size of a number. Additionally, it helps to reduce the risk of mistakes when performing operations involving addition and subtraction.

Tips and Tricks for Solving Advanced Operations with Scientific Notation on a Worksheet

Advanced operations with scientific notation can be challenging to solve on a worksheet, but with a few tips and tricks, they can be mastered with ease.

Firstly, it is important to understand the fundamentals of scientific notation. Scientific notation is a method of expressing numbers that are too large or too small to be conveniently written in standard decimal form. It is expressed in the form ab x 10^n, where ‘a’ is the coefficient, ‘b’ is the base, and ‘n’ is the exponent.

When solving operations with scientific notation on a worksheet, it is helpful to remember that any operation involving the same base will require the coefficients to be added or subtracted and the exponents to remain the same. For example, if you are asked to add 6.21 x 10^7 and 2.53 x 10^7, then the answer would be 8.74 x 10^7.

It is also important to be mindful of the order of operations while solving complex problems. Operations must be completed in the same order as they would be in a standard equation; multiplication or division should be completed before addition or subtraction.

Finally, when multiplying or dividing two numbers in scientific notation, the coefficients should be multiplied or divided and the exponents should be added or subtracted. For example, if you are asked to multiply 3.2 x 10^5 and 4.6 x 10^6, then the answer is 14.72 x 10^11.

By following these tips and tricks, you will be well-prepared to solve advanced operations with scientific notation on a worksheet.

Conclusion

The Operations With Scientific Notation Worksheet is a great tool for students to learn how to use scientific notation and apply it to their daily lives. It provides students with practice in using the concepts of scientific notation and helps them to better understand the basics of the mathematics. With practice, students can become more confident and proficient in using scientific notation in their work. This can help them to become better problem solvers and to better understand the world around them.

[addtoany]