How to Use Measure Of Central Tendency Worksheets to Enhance Your Understanding of Statistics

Measure of central tendency worksheets are a useful tool for students who are learning about statistics. These worksheets help students develop an understanding of the different measures of central tendency and how they are used to assess data.

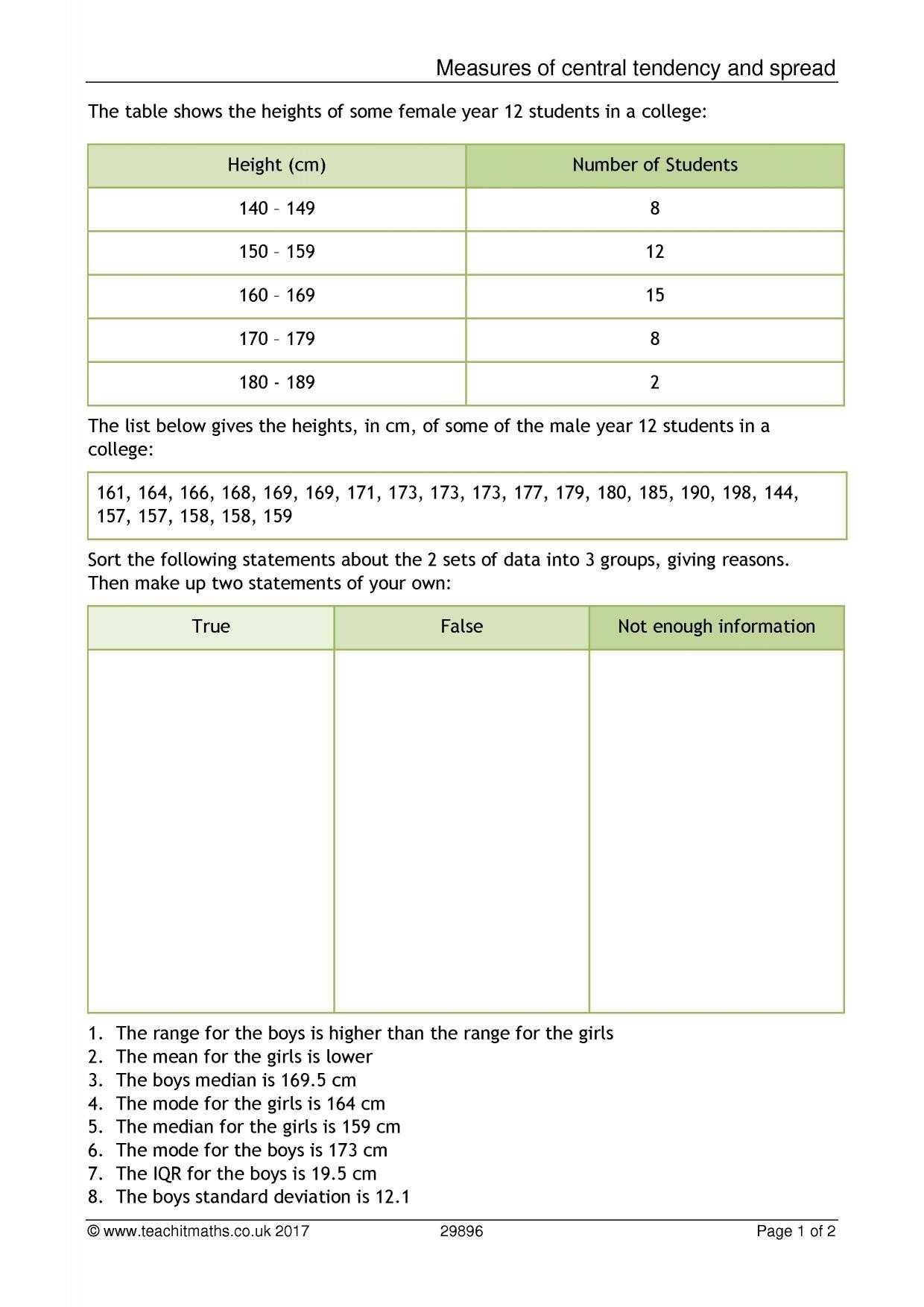
Measures of central tendency are used to describe the average value of a set of data. Three of the most commonly used measures of central tendency are the mean, median, and mode. The mean is the average of the data points, and it is the most commonly used measure of central tendency. The median is the middle value of the data, and it is useful when dealing with data that is not evenly distributed. The mode is the most frequently occurring value in the data set.

Measure of central tendency worksheets provide students with practice calculating the different measures of central tendency. They can also help students understand why the different measures of central tendency are used and how to interpret them. By completing worksheets, students can assess their understanding of measures of central tendency and refine their calculation skills.

Worksheets provide a way for students to practice in a controlled environment. On worksheets, students are given data sets and asked to calculate the mean, median, and mode. They can also be asked to explain why the different measures of central tendency are used for different types of data. This helps them understand when to use each measure and how to interpret it.

Measure of central tendency worksheets also encourage students to think critically about data. For example, students can be asked to explain why a certain measure of central tendency might be more useful for a certain set of data. This encourages them to consider the implications of different measures of central tendency and how to use them to draw meaningful conclusions about data.

By using measure of central tendency worksheets, students can learn how to calculate different measures of central tendency, understand why they are used, and develop their critical thinking skills. These worksheets can be a great way to enhance a student’s understanding of statistics and help them become more proficient in analyzing data.

The Benefits of Understanding Measures of Central Tendency and their Use in Data Analysis

Measures of central tendency are statistical tools used to analyze data sets in order to gain a better understanding of the data. They provide information about the average value or typical value of a data set, allowing one to make inferences about the population from which the data was collected. By understanding and utilizing measures of central tendency, researchers can not only gain a better understanding of the data they are analyzing, but also make informed decisions based on their analysis.

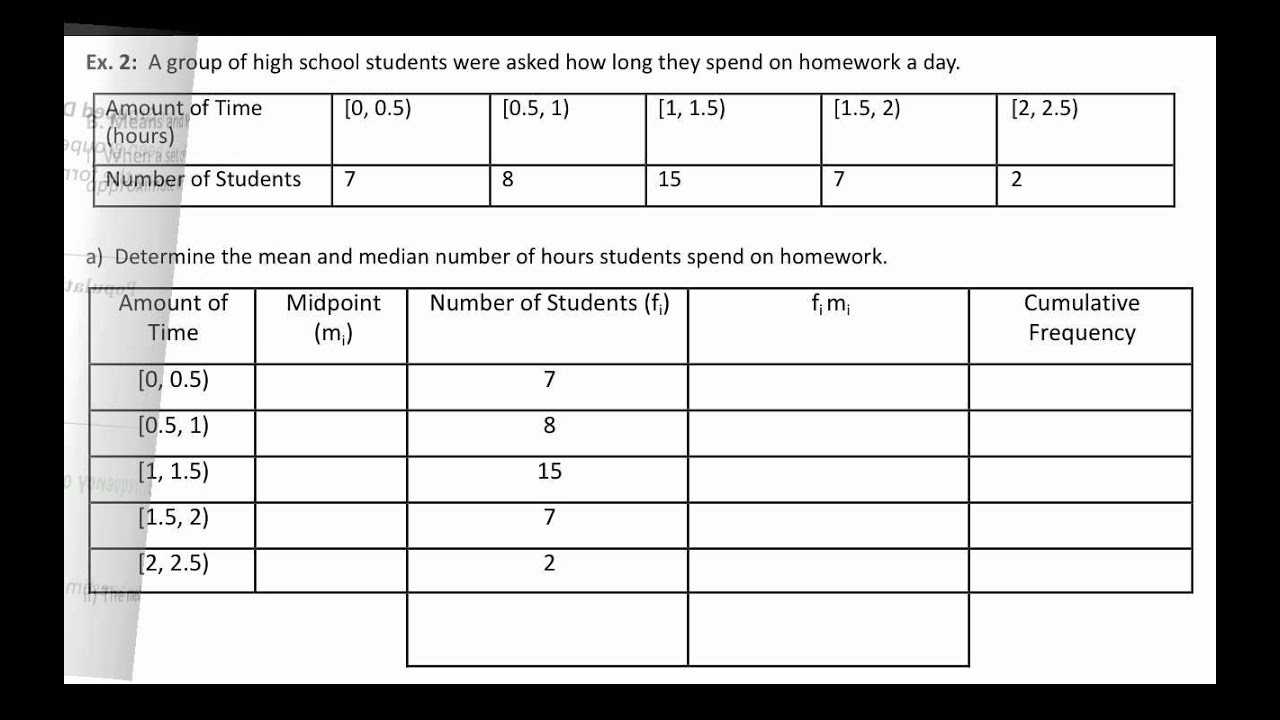
The three most commonly used measures of central tendency are the mean, median, and mode. The mean is calculated by summing all the values within a data set and dividing the total by the number of values. This provides an average value for the data set. The median is the middle value in a data set when the data is sorted from low to high. If there is an even number of values, the median is the average of the two middle values. The mode is the most common value within the data set. It provides a representation of the typical value of the data set.

By understanding and utilizing these measures of central tendency, researchers can gain valuable insights into the data they are studying. For example, if a researcher is studying the heights of a population, they can use measures of central tendency to determine an average height, which can be used to compare the population’s heights to the average. Measures of central tendency can also be used to identify outliers or values that are unusually high or low compared to the rest of the data set. This allows researchers to understand more about the data they are studying and potentially make more accurate predictions.

In conclusion, measures of central tendency are a valuable tool for data analysis. They allow researchers to gain a better understanding of the data they are studying and make informed decisions based on their analysis. By understanding and utilizing measures of central tendency, researchers can gain valuable insights into the data they are analyzing and make more accurate predictions.

Exploring Measures of Central Tendency: What They Are and How to Calculate Them

Measures of central tendency, also known as measures of location or central location, are statistical methods used to determine the central or typical value of a set of data. These measures are important when summarizing and analyzing the characteristics of a population or sample. They provide an indication of the central tendency of the data, which is useful in understanding the overall pattern of the data.

The three most commonly used measures of central tendency are the mean, median, and mode. The mean is the arithmetic average of all of the values in the data set, and is calculated by adding all of the values and dividing by the number of values. The median is the middle value when all of the values are arranged in order from least to greatest, and is found by arranging the data from least to greatest and finding the value in the middle. The mode is the most frequently occurring value in the data set, and is found by counting how often each value occurs in the data set and selecting the value that occurs most often.

In addition to these three measures of central tendency, there are other measures such as the geometric mean, harmonic mean, and trimmed mean. The geometric mean is the nth root of the product of all of the values in the data set, and is used when dealing with ratios or proportions. The harmonic mean is the reciprocal of the arithmetic mean of the reciprocals of the values in the data set, and is used when dealing with ratios or rates. The trimmed mean is the average of a subset of the data that excludes a certain percentage of the highest and lowest values.

Measures of central tendency are important tools for summarizing and analyzing data. They provide an indication of the typical or most common value in a dataset, which can be useful for understanding the overall pattern of the data. By understanding these measures and how to calculate them, one can gain insight into a dataset and use the information to make informed decisions.

The Pros and Cons of Different Measures of Central Tendency and How to Choose the Best One for Your Data

Central tendency measures are used to describe the average value of a set of data. They provide an effective way of summarizing large sets of data and allow us to identify important trends and patterns. There are three main measures of central tendency: the mean, median, and mode. Each measure has its own advantages and disadvantages, and it is important to choose the most appropriate measure for the data set.

The mean is the arithmetic average of a set of numbers; it is calculated by adding up all of the values in the set and dividing by the number of values in the set. This measure is useful for finding the overall trend in a set of data, and it is unaffected by extreme values. However, the mean is sensitive to outliers, and can be heavily influenced by a single data point.

The median is the middle value of a set of numbers; it is calculated by ordering the values from smallest to largest and then selecting the middle value. This measure is useful for identifying the most common value in a set of data, and it is less sensitive to outliers than the mean. However, the median does not take into account the magnitude of each value, so it may not accurately reflect the overall trend in the data.

The mode is the most frequently occurring value in a set of numbers; it is calculated by counting the number of times each value occurs in the set and then selecting the value with the highest count. This measure is useful for identifying the most popular value in a set of data, and it is not affected by extreme values. However, the mode can be heavily influenced by rare values, and it is not appropriate for data sets with multiple modes.

When choosing the best measure of central tendency for a particular data set, it is important to consider the properties of each measure and the characteristics of the data. The mean is usually the most appropriate measure for data sets with symmetrical distributions, while the median is better suited for data sets with skewed distributions. The mode is the most appropriate measure for data sets with multiple modes, such as categorical data. It is also important to consider the presence of outliers, as the mean and median can be heavily influenced by extreme values.

Conclusion

The Measure of Central Tendency Worksheet is a great tool for helping students understand and calculate important measures of central tendency. It provides clear, step-by-step instructions for calculating mean, median, mode, and range, as well as for finding quartiles and percentiles. Additionally, it provides practice questions and examples to help students apply what they have learned. Overall, the Measure of Central Tendency Worksheet is an invaluable resource for students of all ages who are looking to develop a better understanding of these important concepts.