Explaining the Different Types of Graphs Used to Represent Quadratics

Quadratics, or equations of the form ax2 + bx + c = 0, can be represented by several different types of graphs. These include the parabola, the root graph, the vertex form, and the intercept form.

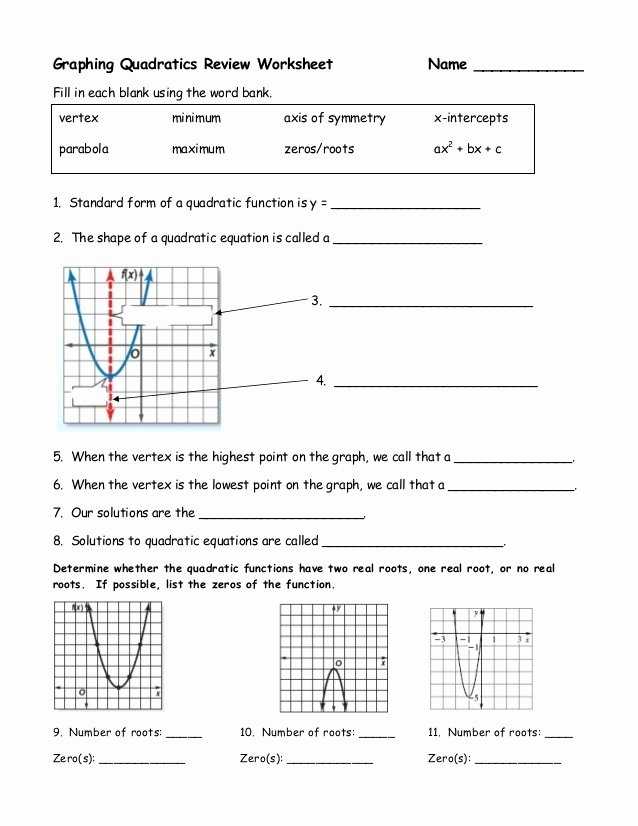
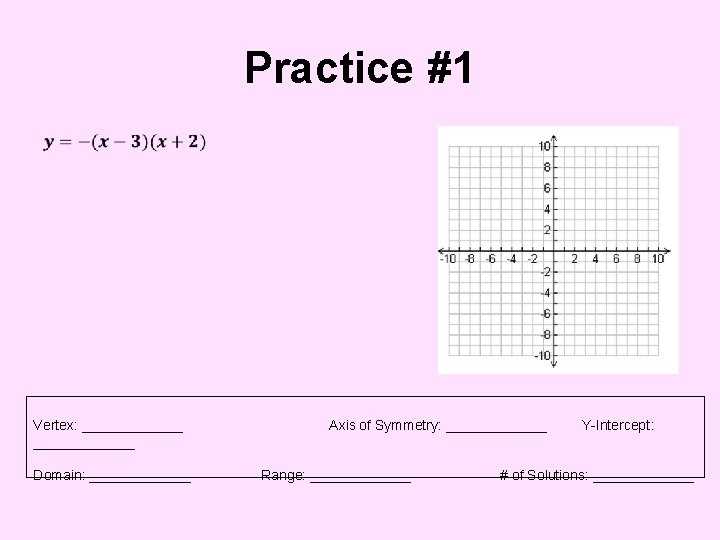
The parabola is probably the most well-known type of graph used to represent quadratics. It is a U-shaped curve that can open up or down, depending on the sign of the coefficient of the squared term (a). This graph is useful for visualizing the solutions of a quadratic equation, or the points at which the equation is equal to zero.

The root graph is a line graph used to represent the roots of a quadratic equation. The roots of a quadratic equation are the points at which the equation is equal to zero, and these points can be found by solving the equation. The root graph plots these points on an x-y graph, with the x-axis representing the solutions and the y-axis always having a value of zero.

[toc]

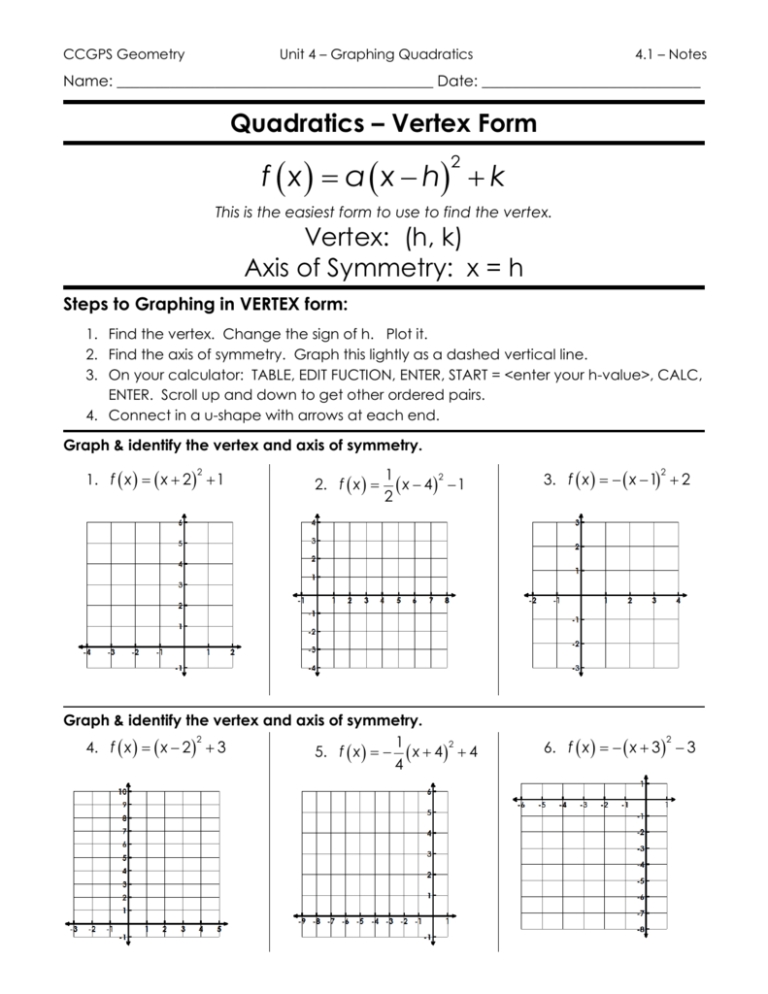
The vertex form of a graph is an equation of the form y = a(x – h)2 + k, which is used to represent the vertex of a parabola. This graph is useful for finding the coordinates of the vertex (the maximum or minimum point of the parabola).

The intercept form of a graph is an equation of the form y = ax2 + bx + c, which is used to represent the x-intercepts of a parabola. This graph is useful for finding the points at which the parabola intersects the x-axis (the solutions of the equation).

Overall, these four types of graphs are all useful for representing quadratics, each in their own way. By understanding the different types of graphs used to represent quadratics, one can gain a better understanding of the equations and the solutions they represent.

Strategies for Solving Graphing Quadratics Review Worksheets

The graphing of quadratics is an important skill to master in mathematics. It involves a few different techniques that can be used to solve a variety of problems. Here are some strategies for solving graphing quadratics review worksheets:

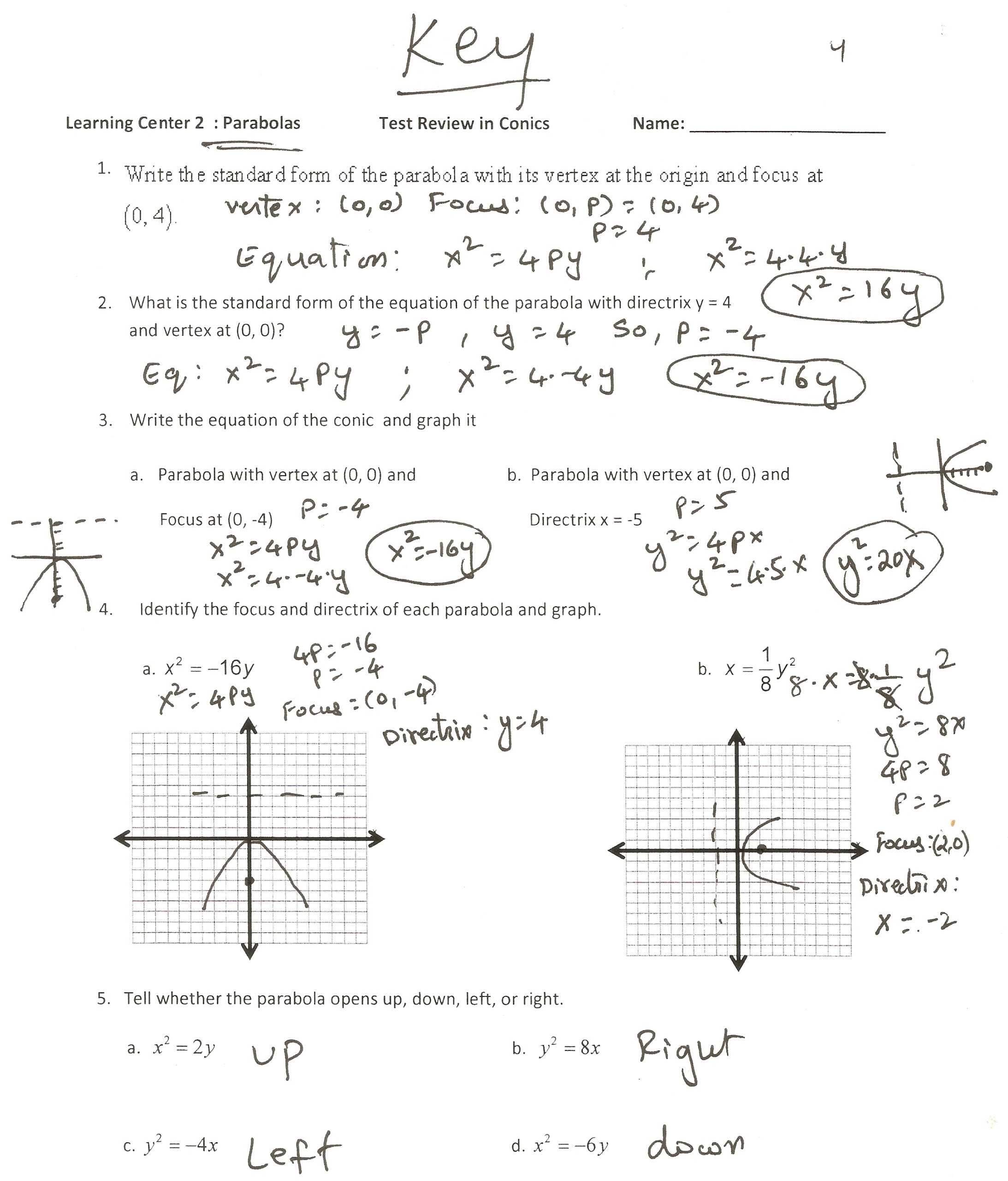
1. Factoring: Factoring is a process of breaking down an expression into simpler parts. It uses the distributive property to simplify the terms of the expression and create a quadratic equation. This equation can then be solved by using the methods of completing the square, quadratic formula, or factoring.

2. Completing the Square: Completing the square is a technique that can be used to solve quadratic equations. It involves taking a polynomial equation and transforming it into a form that can be easily graphed. The steps involve adding a constant to both sides of the equation and then finding the square root of both sides.

3. Quadratic Formula: The quadratic formula is a formula that can be used to solve a quadratic equation. It uses the coefficients of the quadratic equation to determine the x-intercepts and the vertex of the graph.

4. Graphing: Once the x-intercepts and vertex have been determined, the graph of the quadratic equation can be drawn. This involves plotting points on a graph and connecting them with a smooth curve.

These are just a few strategies for solving graphing quadratics review worksheets. It is important to remember that each problem may require a different approach and it is important to understand the different methods. With practice and patience, students can become proficient at solving these types of problems.

Utilizing Technology to Facilitate Graphing Quadratics Review Worksheets

The quadratic equation is a fundamental component of mathematics that is taught to students in secondary school, and for many the graphing of quadratics is a difficult task. With modern technology, however, the difficulty of graphing quadratics can be alleviated. Utilizing a variety of technological tools, teachers can help their students to more easily understand the process of graphing quadratics, and provide review worksheets to ensure that learning is successful.

Interactive graphing programs can be used to demonstrate the process of graphing quadratics. These programs can be used to show students how to identify the vertex, intercepts, and symmetries of a graph, as well as how to identify the equation that corresponds with a given graph. Interactive graphing programs can also be used to generate quadratic equations for students to graph. Through the use of these programs, students can better understand the process of graphing quadratics, and make the process less intimidating.

In addition to interactive graphing programs, there are a variety of other technological tools that can be used to facilitate the learning of graphing quadratics. For example, online graphing calculators can be used to help students graph equations quickly and accurately. These calculators can also be used to generate quadratics for students to graph. Additionally, online quizzes and review worksheets can be used to help students master the material. These worksheets can be tailored to the needs of the students, and can be used to ensure that learning is successful.

Technology can be a valuable tool for teaching students how to graph quadratics. By utilizing interactive graphing programs, online graphing calculators, and online review worksheets, teachers can ensure that their students have the resources necessary to gain a thorough understanding of the process of graphing quadratics. Through the use of technology, students can more easily and successfully learn how to graph quadratics, and teachers can help their students to master the material.

Conclusion

Overall, graphing quadratics can be a challenging but rewarding task. It is important to remember the key points such as the vertex and axis of symmetry, as well as the basic shapes of quadratic graphs. With practice and patience, graphing quadratics can become second nature. With the help of this review worksheet, students can strengthen their graphing skills and become more confident in their mathematical abilities.

[addtoany]