Analyzing Graphs of Piecewise Functions: A Step-by-Step Worksheet Tutorial

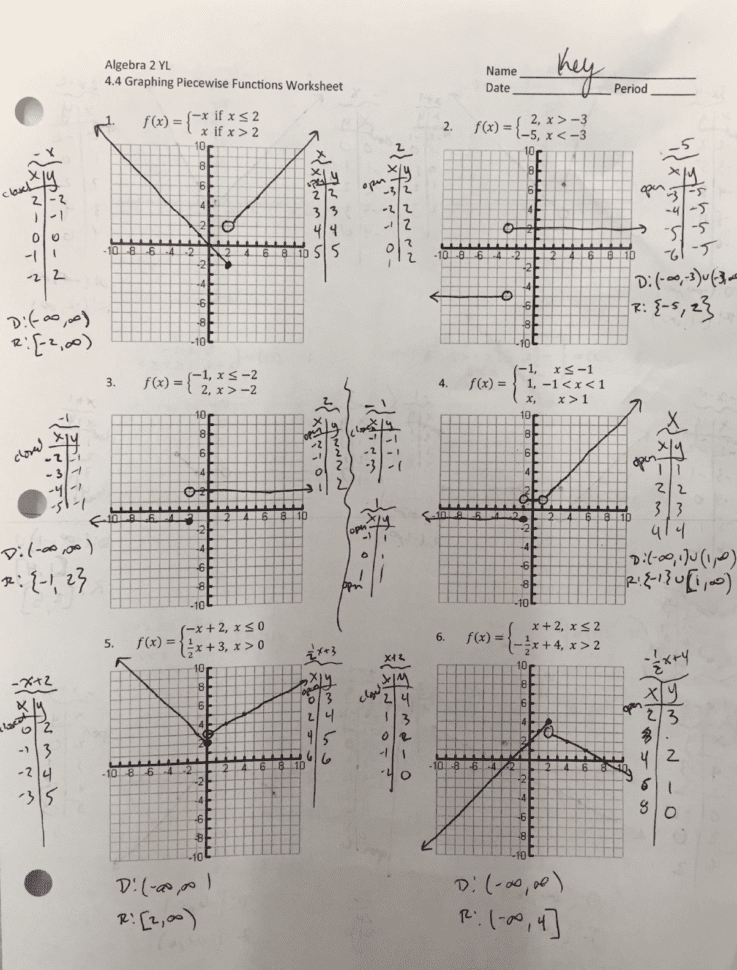
Welcome to this step-by-step worksheet tutorial on analyzing graphs of piecewise functions. Piecewise functions are a class of functions composed of two or more parts, each of which is defined on a different interval. In this tutorial, we will be looking at how to analyze the graphs of these types of functions, which can be quite tricky.

Before we begin, it is important to understand the basic components of a piecewise function. A piecewise function consists of two or more parts that are each defined on a different interval. In order to graph a piecewise function, we must first identify the intervals on which each part of the function is defined. Then, we must identify the equation for each part of the function. Once we have these pieces of information, we are ready to graph the function.

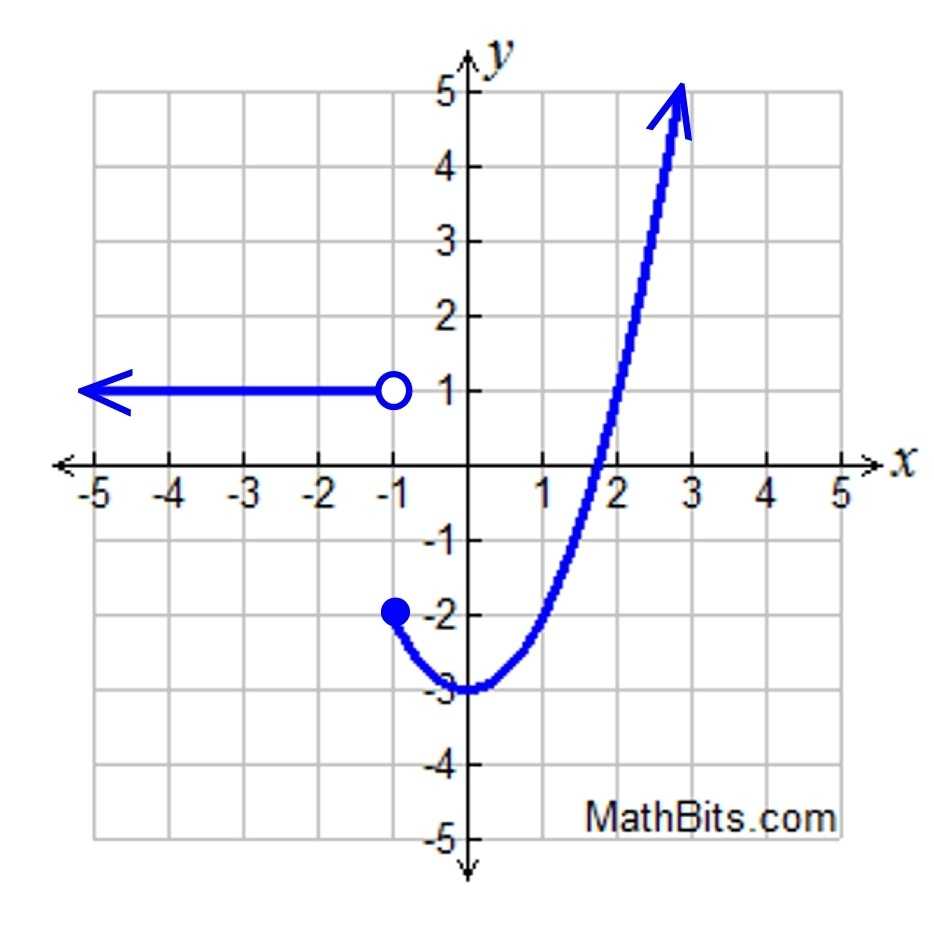
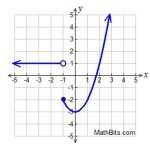
Now let’s look at an example. Consider the piecewise function f(x) = { x^2 + 2, if x ≤ 0; x + 3, if x > 0 }.

[toc]

First, we need to identify the intervals on which each part of the function is defined. In this case, the first part of the function is defined on the interval x ≤ 0 and the second part is defined on the interval x > 0.

Next, we need to identify the equations for each part of the function. The equation for the first part is x^2 + 2, and the equation for the second part is x + 3.

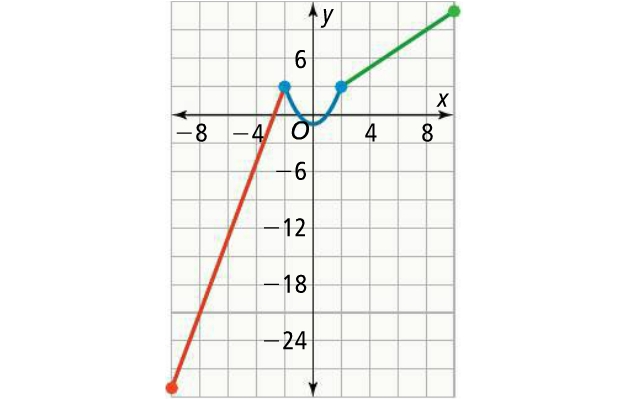
Now we are ready to graph the piecewise function. To do this, we will start by plotting the two points that are defined on the interval x ≤ 0. In this case, these points are (0,2) and (-1,3). We will then draw a line connecting these points. The resulting graph is shown below.

Finally, we need to plot the point that is defined on the interval x > 0. In this case, the point is (1,4). We will then draw a line connecting this point to the line we have already drawn. The resulting graph is shown below.

We have now successfully graphed the piecewise function f(x) = { x^2 + 2, if x ≤ 0; x + 3, if x > 0 }. As you can see, graphing piecewise functions can be quite tricky, but with practice and patience, you can learn how to do it.

Exploring the Different Types of Piecewise Functions and Their Graphical Representations

Piecewise functions are a type of mathematical function composed of multiple individual functions that are defined over specific intervals in the domain. The definition of these functions is piecewise, meaning that each function is defined over different intervals and the number of functions and intervals depend on the specific problem at hand. Depending on the complexity of the problem, a piecewise function can be linear, polynomial, exponential, or even rational.

Graphically, piecewise functions look like a combination of multiple lines, curves, or other shapes. Each individual function is plotted in its own interval and, depending on the nature of the function, may be continuous or discontinuous. The points of discontinuity are known as ‘knots’ and they occur when two or more functions meet.

Linear piecewise functions are composed of two or more linear functions that are defined over different intervals. The domain of a linear piecewise function is divided into multiple regions and each region is represented by a linear equation. The graph of a linear piecewise function is composed of multiple line segments, each of which represents a different linear equation.

Polynomial piecewise functions are composed of two or more polynomial functions that are defined over different intervals. The graph of a polynomial piecewise function is composed of multiple polynomial curves, each of which represents a different polynomial equation. Depending on the nature of the problem, the polynomial curves may be continuous or discontinuous.

Exponential piecewise functions are composed of two or more exponential functions that are defined over different intervals. The graph of an exponential piecewise function is composed of multiple exponential curves, each of which represents a different exponential equation. Depending on the nature of the problem, the exponential curves may be continuous or discontinuous.

Rational piecewise functions are composed of two or more rational functions that are defined over different intervals. The graph of a rational piecewise function is composed of multiple rational curves, each of which represents a different rational equation. Depending on the nature of the problem, the rational curves may be continuous or discontinuous.

In conclusion, piecewise functions are a type of mathematical function composed of multiple individual functions defined over specific intervals in the domain. Graphically, piecewise functions look like a combination of multiple lines, curves, or other shapes. Depending on the complexity of the problem, a piecewise function can be linear, polynomial, exponential, or even rational.

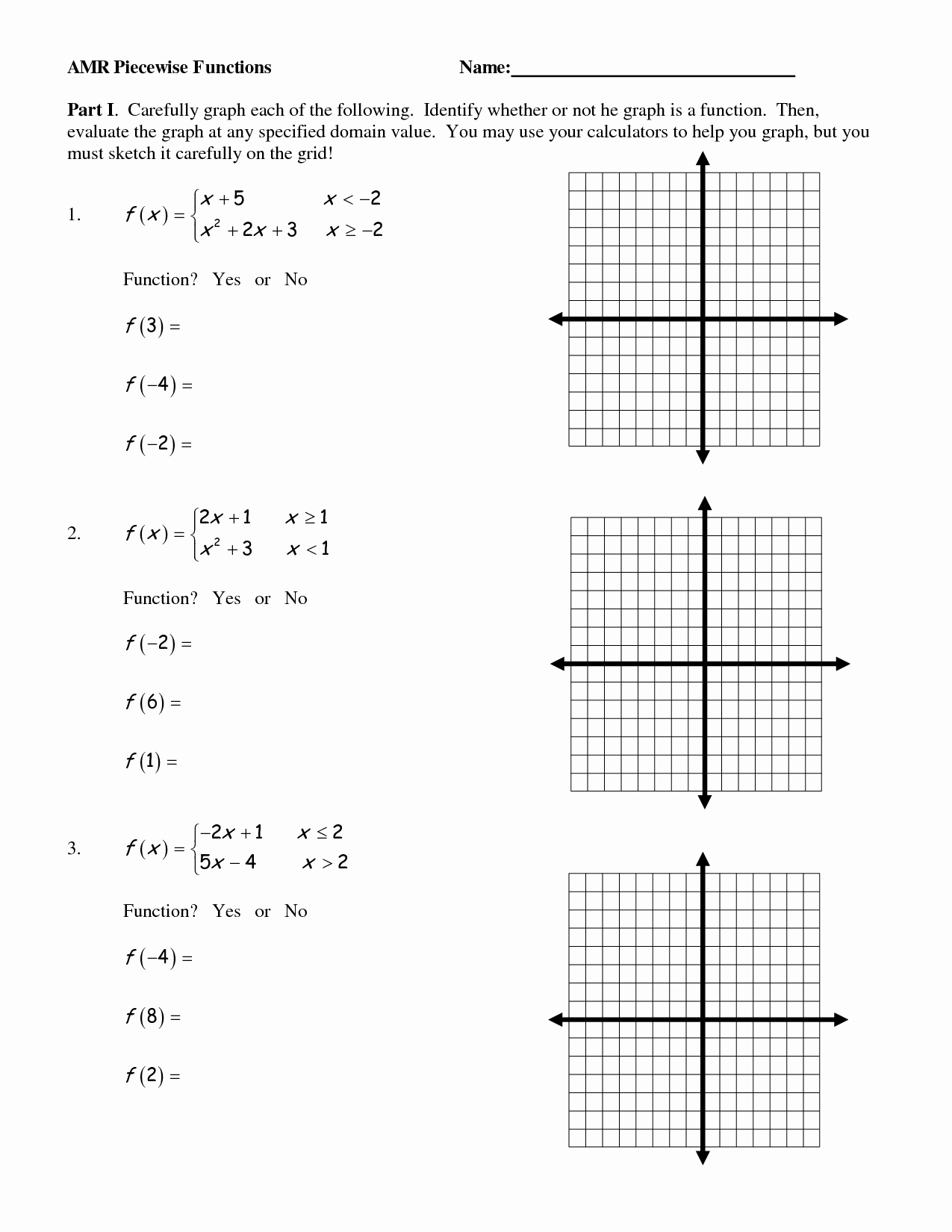
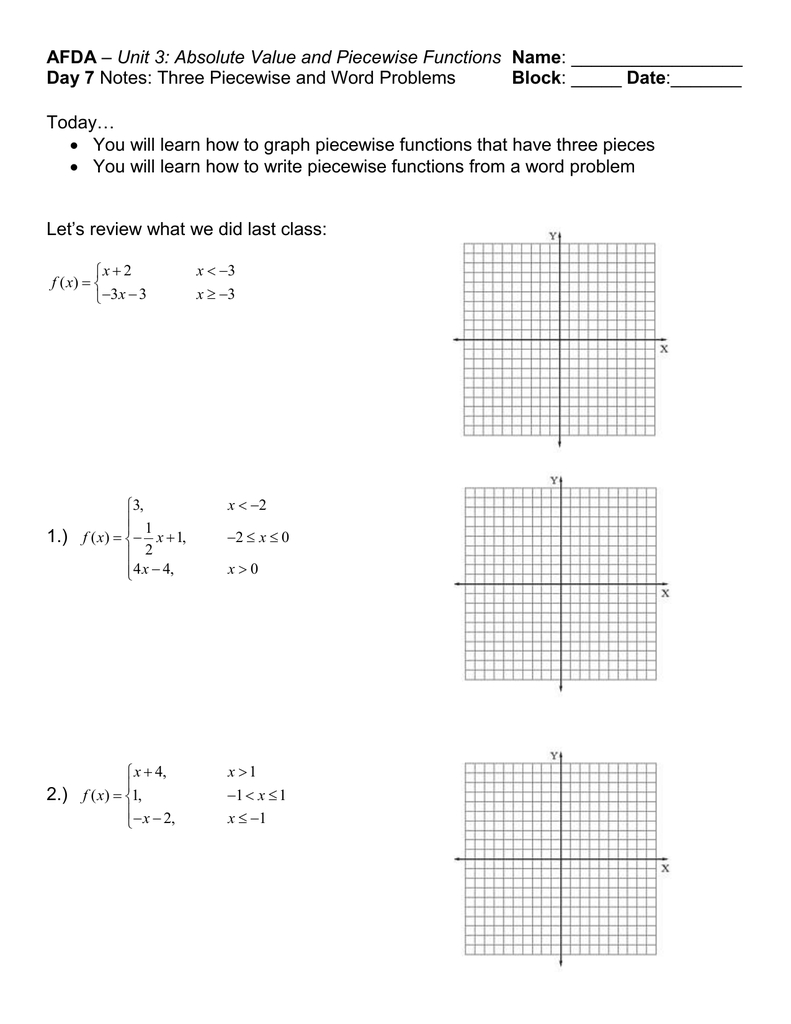
Examining How to Solve Piecewise Functions: An Interactive Worksheet Approach

This worksheet aims to provide an interactive approach to help students understand how to solve piecewise functions. Piecewise functions are a type of function that can take on different values or behaviors depending on the value of the independent variable. This type of function is often seen in calculus problems, as well as in algebra and trigonometry.

The worksheet begins with a brief introduction to piecewise functions, including the definition and some examples. This is followed by a series of questions that lead the student through the steps of solving a piecewise function. Each step is accompanied by an example that helps the student understand the concept being taught.

The worksheet then provides the students with an opportunity to practice what they have learned. This is done by providing a piecewise function for the students to solve. The worksheet provides hints and prompts to help the students work through the problem. Once the students have worked through the problem, the worksheet provides an opportunity for them to check their solution with a provided answer key.

The worksheet also provides a variety of additional resources for the student. These include a description of the various types of piecewise functions, as well as a list of terms and definitions related to the topic. This helps to ensure that the student has a solid understanding of the material.

Through this interactive worksheet approach, students will gain a better understanding of how to solve piecewise functions. The worksheet is designed to be user friendly, allowing the student to work through the material at their own pace. With this approach, students will be able to gain the skills necessary to confidently and accurately solve a variety of piecewise functions.

Conclusion

The Graphing Piecewise Functions Worksheet is an excellent resource for students to practice and build their understanding of graphing piecewise functions. Through practice, students will be able to identify the different pieces of a piecewise function, graph the function, and identify the domain and range of the function. Additionally, the worksheet helps to reinforce the basic principles of graphing and can be used to assess the student’s understanding of the topic.

[addtoany]