How to Utilize a Graphing Absolute Value Equations Worksheet to Develop an Understanding of Graphs

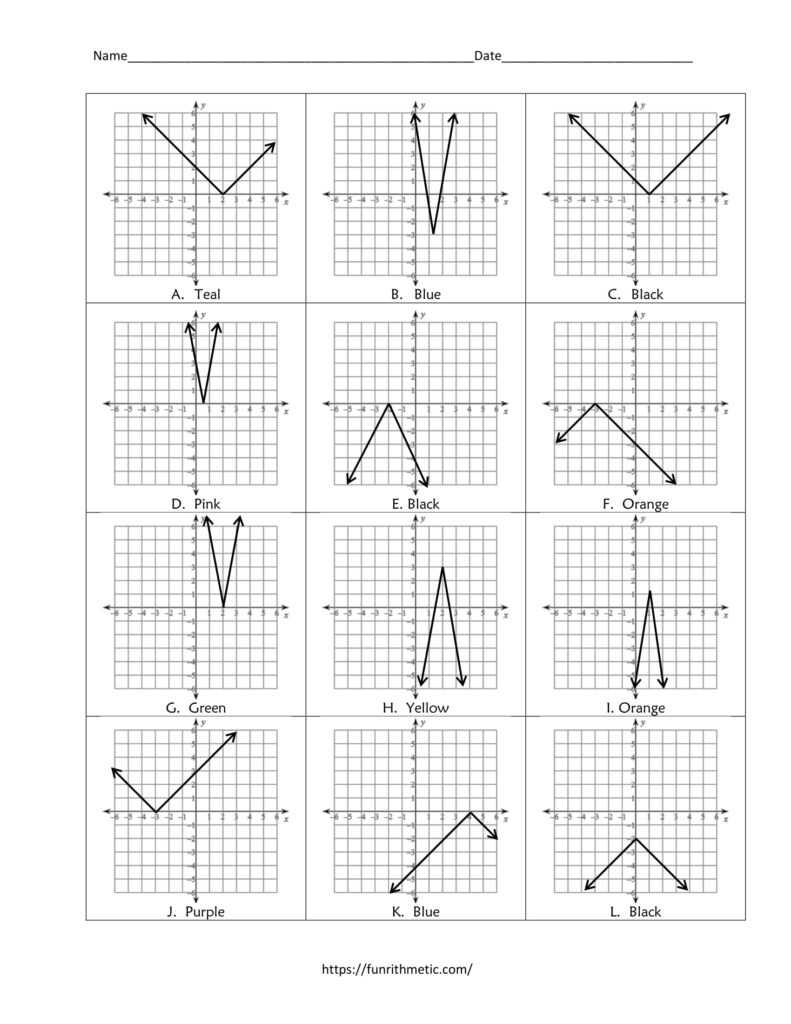
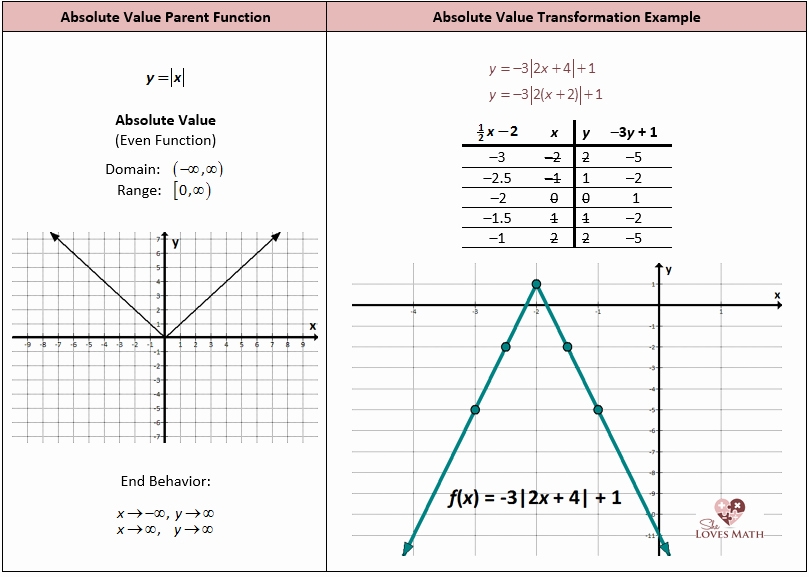
A graphing absolute value equations worksheet is an effective tool for developing an understanding of graphs. This resource can help students learn how to graph absolute value equations, identify key features of the graph, and interpret the graph to draw conclusions about the equation.

When using a graphing absolute value equations worksheet, it is important to first build an understanding of the equation and its components. This can be done by having students identify the equation, determine the range of values that the equation represents, and identify the key features of the equation, such as the y-intercept, the asymptote, and the slope. Once students have a basic understanding of the equation, they can begin to graph the equation. To do this, they must plot points on the graph that represent the values of the equation and then connect the points to form a line.

Once students have graphed the equation, they can look at the graph to determine key characteristics. Students should look for the y-intercept and the asymptote, as well as the slope of the line. They should also be able to recognize when the equation has an even or odd symmetry. By recognizing these characteristics, students can draw conclusions about the equation and how it behaves in different contexts.

Finally, students should be able to interpret the graph to draw conclusions about the equation. This includes determining the maximum and minimum values of the equation, as well as determining how the equation behaves in relation to other equations. By interpreting the graph, students can understand how the equation behaves and how it can be used in various contexts.

By using a graphing absolute value equations worksheet, students can develop an understanding of graphs and how to graph absolute value equations. This resource can help students understand the components of the equation, graph the equation, recognize key features, and interpret the graph to draw conclusions. By utilizing this worksheet, students can learn how to graph an equation and use it in different contexts.

Exploring the Differences Between Linear and Nonlinear Graphs with a Graphing Absolute Value Equations Worksheet

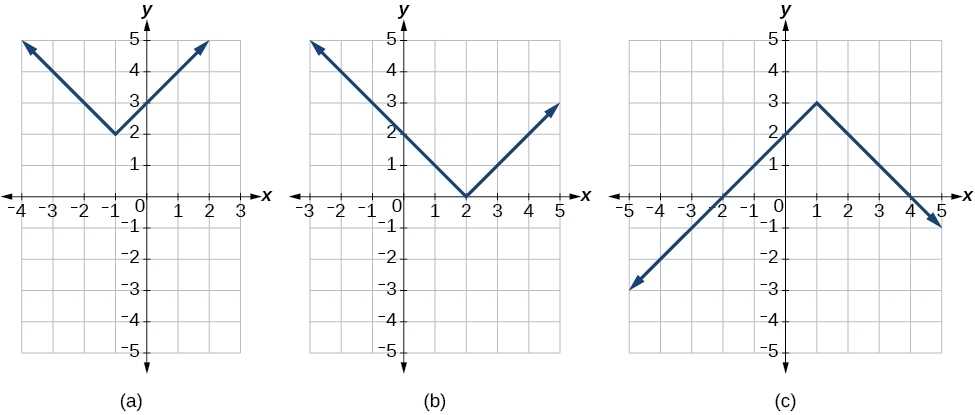
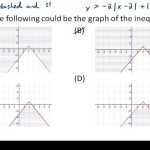
When it comes to graphing equations, it is important to understand the differences between linear and nonlinear graphs. Linear equations produce straight lines when graphed, while nonlinear equations often produce curved graphs. To illustrate this, let us look at a graphing absolute value equations worksheet.

The worksheet provides a number of equations that involve the absolute value function. We can see from the worksheet that each equation produces a different type of graph. The linear equations produce a straight line, while the nonlinear equations produce curves.

The linear equations are graphed by plotting the x and y values that the equation produces. As you move the x value along the x-axis, the y value changes in a linear fashion. This means that if you increase the x value, the y value increases in a consistent manner. Conversely, if you decrease the x value, the y value decreases in a consistent manner.

On the other hand, the nonlinear equations are graphed by plotting the x and y values that the equation produces. As you move the x value along the x-axis, the y value changes in a nonlinear fashion. This means that if you increase the x value, the y value does not necessarily increase in a consistent manner. Similarly, if you decrease the x value, the y value does not necessarily decrease in a consistent manner.

The worksheet also provides an example of how to graph each equation. For the linear equations, the slope is given and the point where the line crosses the y-axis is also provided. For the nonlinear equations, the slope is not given and the points where the graph crosses the y-axis are usually not provided.

By analyzing the graphing absolute value equations worksheet, we can see that linear equations produce straight lines when graphed, while nonlinear equations often produce curved graphs. This is due to the fact that the x and y values of the equation change in different ways. Knowing the differences between linear and nonlinear graphs can help us understand how different equations can be graphed.

Strategies for Solving Absolute Value Equations Through Graphing and a Graphing Absolute Value Equations Worksheet

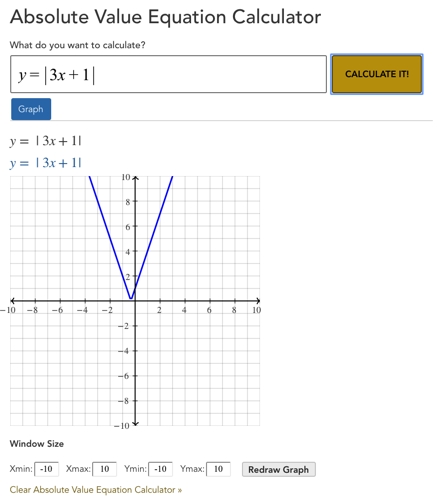
Graphing absolute value equations is a great way to find their solutions. To do so, one must first plot the equation on a graph. This can be done by creating a table of x- and y-values, plotting the points, and connecting them with a line.

Once the graph is complete, the solutions can be found by examining the graph. In general, the solutions are the points of intersection between the graph and the x-axis. The x-axis is the line of symmetry for absolute value equations, so the solutions are the points at which the graph crosses the line of symmetry.

To aid students in solving absolute value equations through graphing, a graphing absolute value equations worksheet can be used. This worksheet should provide students with the equation, a table of x- and y-values, a graph, and directions on how to use the graph to find the solutions.

By working through the graphing absolute value equations worksheet, students will gain invaluable experience in solving absolute value equations through graphing. This skill is essential for many mathematics courses, as absolute value equations are often used in calculus and other higher-level courses.

With the help of a graphing absolute value equations worksheet, students will be able to develop a strong foundation in solving absolute value equations through graphing. This foundation is the key to successful problem-solving in mathematics.

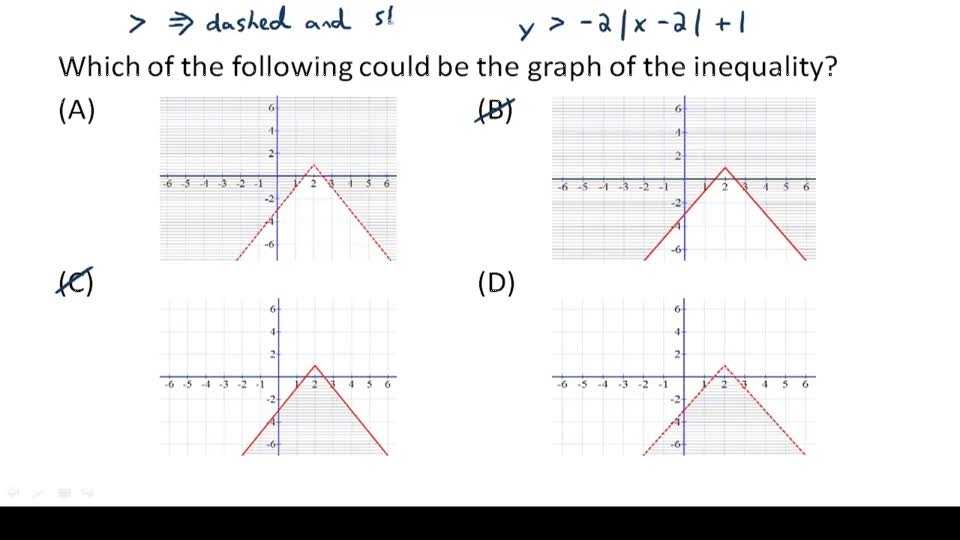
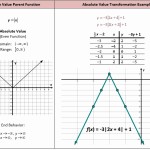
Understanding the Impact of the Slope and Intercept on Graphs Using a Graphing Absolute Value Equations Worksheet

When graphing absolute value equations, the slope and intercept of the equation can have a significant impact on the shape of the graph. The slope of the equation defines the steepness of the line, while the intercept is the point at which the line intersects the x-axis. Understanding how these two factors affect the shape of the graph can be helpful in interpreting the results of the equation.

The slope of the equation is determined by the coefficient of x in the equation. If the coefficient is positive, then the graph will have a positive slope, and if the coefficient is negative, then the graph will have a negative slope. A positive slope indicates that the graph is rising, while a negative slope suggests that the graph is falling. The steepness of the line is determined by the magnitude of the coefficient. The larger the coefficient, the steeper the line will be.

The intercept of the equation is determined by the constant term in the equation. The intercept is the point at which the line intersects the x-axis. If the constant term is positive, then the graph will have a positive intercept, and if the constant term is negative, then the graph will have a negative intercept. The intercept will determine where the graph begins its ascent or descent.

By understanding how the slope and intercept of an absolute value equation affects the shape of the graph, it becomes easier to interpret the results of the equation. By manipulating the coefficient and constant term of the equation, one can change the slope and intercept of the graph, thus creating a different shape. Inspecting how these two factors interact with one another will provide an improved understanding of how the equation impacts the graph.

Conclusion

Overall, graphing absolute value equations worksheet is an effective tool for helping students understand the concept of graphing absolute value equations. Through the use of this worksheet, students can gain an understanding of the various methods used to graph these equations. Additionally, this worksheet can be used to reinforce the knowledge of graphing and help students develop a deeper understanding of the topic. By using this worksheet, students can also practice graphing equations on their own and become more confident in their graphing skills.