How to Use a Geometric Sequences Worksheet to Find the Solution to Your Math Problems

Finding the solution to a math problem can be a daunting task, but using a geometric sequences worksheet can make it much easier. Geometric sequences are equations in which each term is calculated by multiplying the previous term by a constant number. Using a geometric sequences worksheet can help you find the solution to your math problem by breaking it down into manageable pieces.

The first step when using a geometric sequences worksheet is to identify the geometric sequence that is being used in the problem. Once you have identified the sequence, you will need to list out the terms of the sequence using the formula provided. It is important to note that the first term of the sequence is usually listed as “1”. Once you have listed out the terms of the sequence, you will need to identify the constant number, or “r”, that is being used to calculate each successive term of the sequence.

Once you have identified the terms of the sequence and the constant number, you can begin to solve the math problem. To do this, you will need to use the formula provided in the worksheet. This formula will tell you what the value of the nth term is. For example, if the formula provided is “an = arn-1”, then the value of the fourth term in the sequence would be “a4 = a3r”.

After you have solved the math problem using the geometric sequences worksheet, you can then use the answer to check your work. To do this, you will need to substitute the values that you have calculated into the original equation and make sure that the answer is correct. If there is a discrepancy, you will need to go back and adjust the values that you have calculated.

Using a geometric sequences worksheet can be a great way to find the solution to your math problems. By breaking the problem down into smaller parts and checking your work, you can be sure that you have the correct answer.

Exploring the Different Types of Geometric Sequences and Their Answers

A geometric sequence is a sequence of numbers in which each successive term is obtained by multiplying the previous term by a fixed non-zero number, called the common ratio. This type of sequence can be expressed in the form a, ar, ar2, ar3, ar4, …, where a is the first term of the sequence and r is the common ratio. Geometric sequences have many interesting applications in mathematics, science, and engineering.

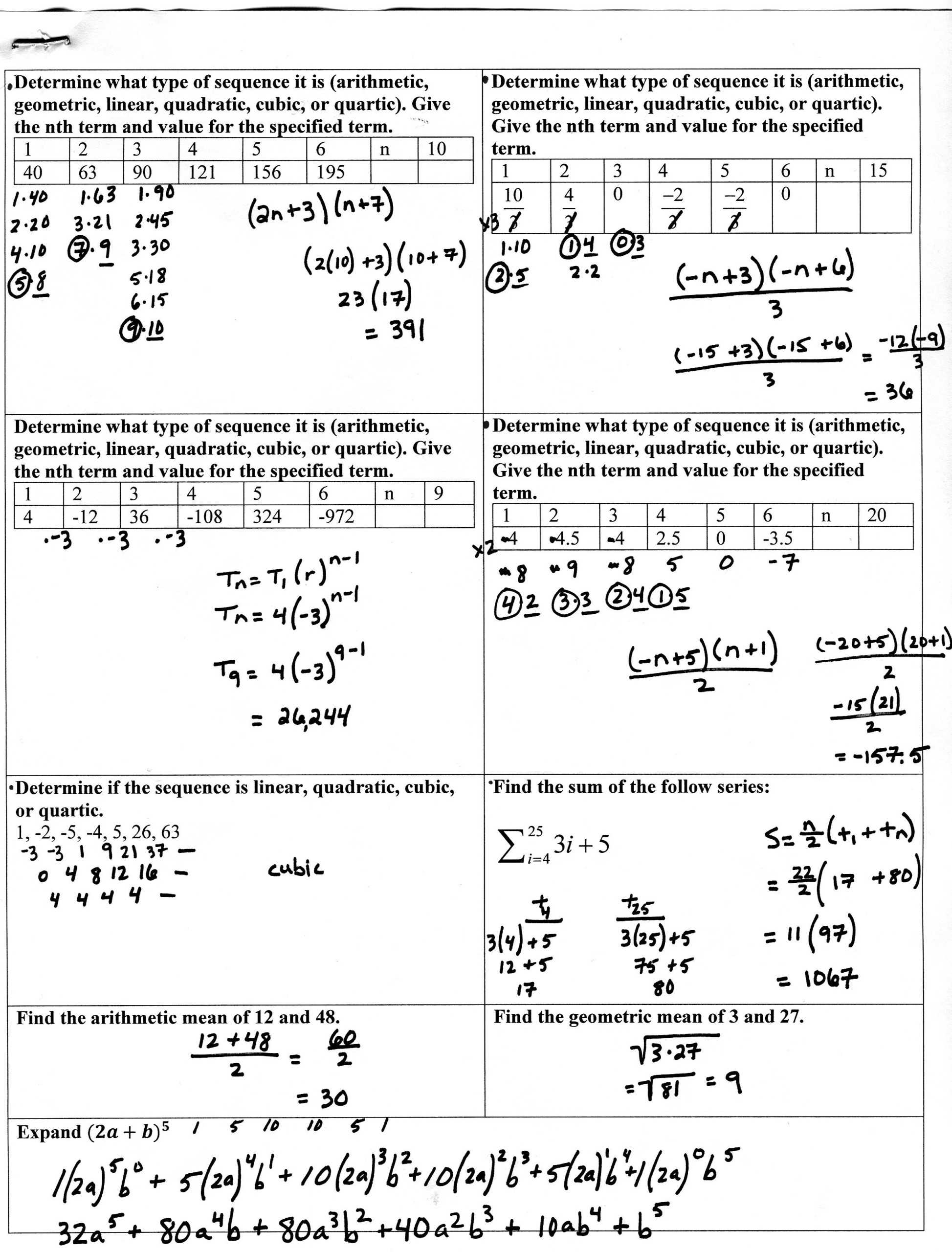
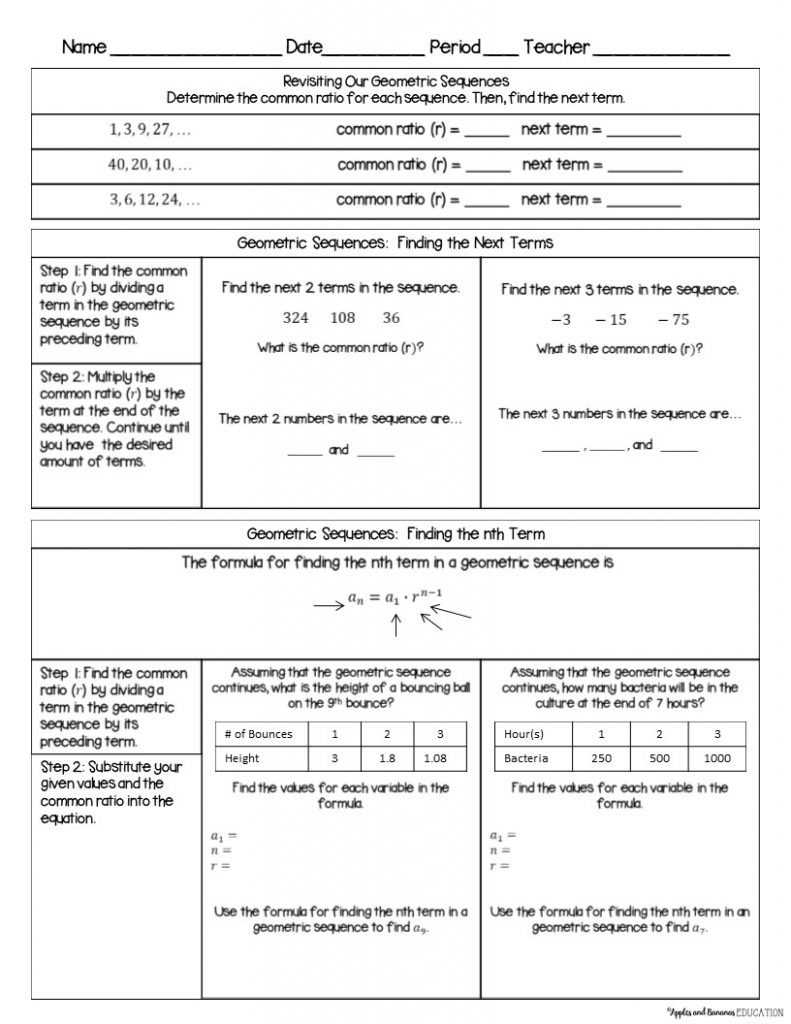
The answer to a geometric sequence can be expressed as a general formula: an = arn–1, where a is the first term of the sequence and r is the common ratio. This formula can be used to calculate the nth term of any geometric sequence, provided the first term and the common ratio are known.

Geometric sequences can be classified into three main types: finite, infinite increasing, and infinite decreasing. A finite geometric sequence is one in which the common ratio is between 0 and 1, and the sequence eventually reaches a maximum or minimum value. An infinite increasing geometric sequence is one in which the common ratio is greater than 1 and the sequence continues to increase without bound. An infinite decreasing geometric sequence is one in which the common ratio is between 0 and 1 and the sequence continues to decrease without bound.

In general, the answer to a finite geometric sequence is the sum of the first n terms, where n is the number of terms in the sequence. For infinite geometric sequences, the answer can be expressed as a limit. For increasing sequences, the limit is infinity, and for decreasing sequences, the limit is zero.

Geometric sequences can be used to model a wide variety of phenomena, from population growth to interest rates. By understanding the different types of geometric sequences and their answers, it is possible to gain insight into many real-world situations.

Unlocking the Secrets of Geometric Sequences with an Interactive Worksheet and Its Answers

Geometric sequences are one of the most interesting and important topics in mathematics. With this interactive worksheet, students can unlock the secrets of geometric sequences and gain an understanding of how they work.

The worksheet begins by explaining what a geometric sequence is and how to identify one. It then provides an example of a geometric sequence and explains how to calculate the common ratio. This is followed by a series of questions which introduce the concept of a geometric sequence and apply the calculation of the common ratio to various examples.

The questions are designed to be interactive and self-checking, so that students can track their own progress. After completing the questions, students can check the answers provided at the end of the worksheet. This provides students with instant feedback and helps them to understand the concepts more quickly.

By working through this interactive worksheet, students can gain an understanding of the basic principles of geometric sequences and be able to apply them in real life. With its engaging and interactive design, this worksheet is an excellent tool for helping students unlock the secrets of geometric sequences.

Conclusion

In conclusion, the Geometric Sequences Worksheet Answers provide an excellent way for students to gain an understanding of geometric sequences and their properties. Through completing this worksheet, students have been able to learn how to identify the common ratio and the nth term, as well as how to use the formula for the nth term to calculate a specific term. Additionally, students have been able to practice finding the sum of a finite geometric sequence. All of these skills will be essential in further math courses.