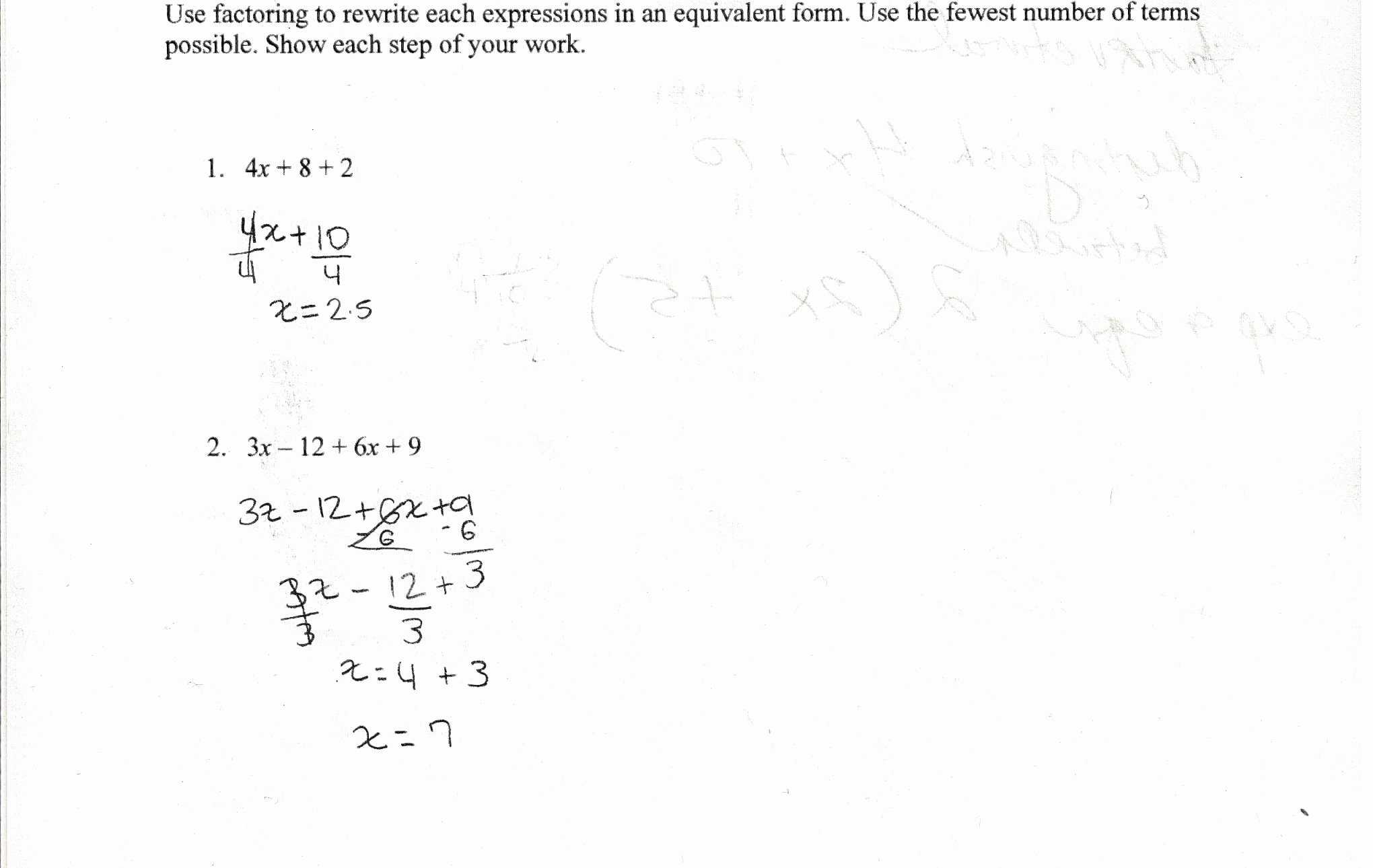Unpacking the Basics of Factoring Distributive Property Worksheets: A Beginner’s Guide

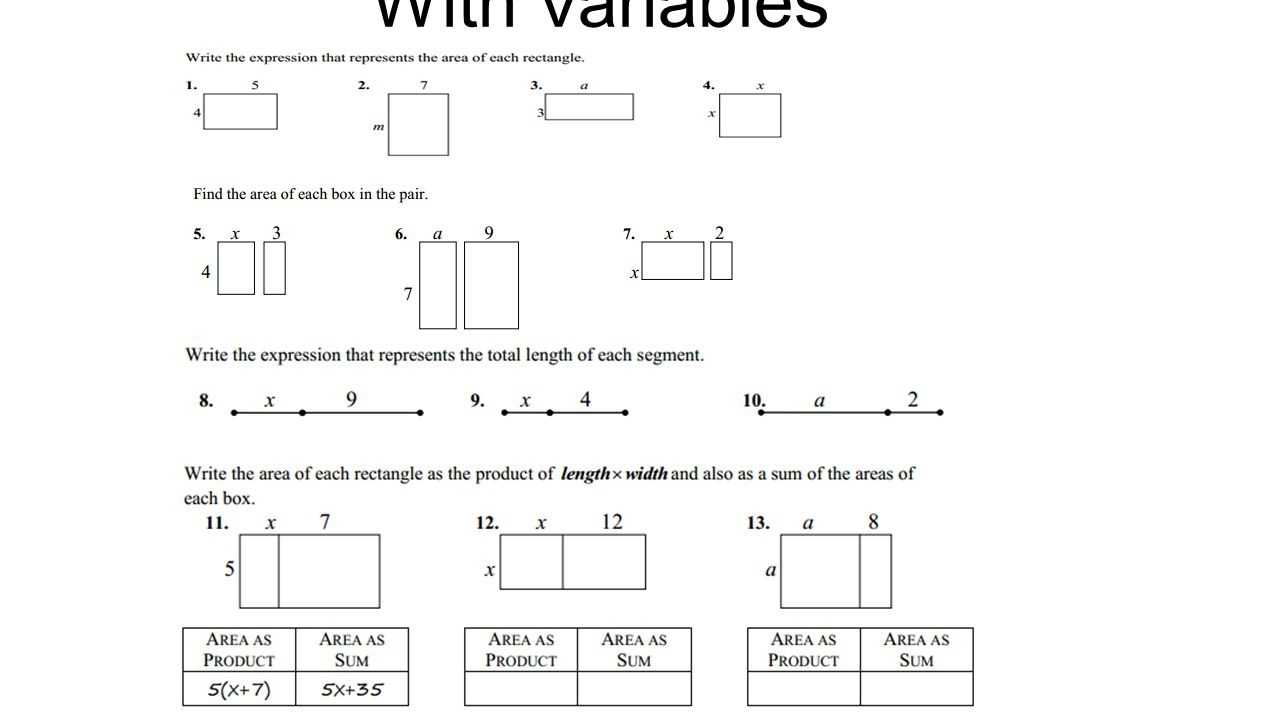
Factoring distributive property worksheets are a great way to help students learn and review important math concepts. These worksheets break down the distributive property into small chunks that are easier to understand and solve. By breaking the property down into individual steps, it allows students to practice and develop their skills in a more efficient manner.

The basic concept of the distributive property is that it states that the multiplication of a sum by a number is equal to the sum of the multiplication of each addend by the same number. For example, if a student is asked to simplify the expression “4 × (5 + 6)”, the answer would be “4 × 5 + 4 × 6”. This is because the distributive property states that the multiplication of a sum by a number is equal to the sum of the multiplication of each addend by the same number.

When introducing the distributive property to students, it is important to first explain how it works. Once students understand this concept, they can begin to practice and apply it. Factoring distributive property worksheets are a great way to help students understand and practice this concept.

These worksheets typically consist of a series of problems that ask students to simplify equations using the distributive property. The worksheets typically start off with simpler equations, then move on to more complicated ones. This allows students to gradually increase their understanding of the property as they progress through the worksheets.

Factoring distributive property worksheets are an important tool for students who are learning or reviewing the concept. They provide an effective way for students to practice their new skills and develop a deeper understanding of the distributive property.

Tips for Understanding and Mastering Factoring Distributive Property Worksheets

1. Review the Basics: Before attempting to work on factoring distributive property worksheets, it is important to ensure that you are familiar with the basic concepts related to factoring. Review the definition of factoring and the distributive property, as well as how the two interact.

2. Understand the Problem: Read through the instructions provided on the worksheet carefully and make sure that you understand what is being asked of you. If there is any confusion, do not hesitate to ask your teacher for clarification.

3. Identify the Key Terms: Take a moment to identify the key terms that are used in the problem. This will help you to better understand the underlying concept that you are being asked to solve.

4. Work Through the Problem: Once you have a good understanding of the problem, work through the steps provided on the worksheet. It is important to show your work so that it can be easily checked.

5. Check Your Answers: Once you have finished working through the problem, check your answer against the answer key provided on the worksheet. This will help you to identify any mistakes and improve your understanding of the concept.

6. Practice: As with any math topic, the best way to master factoring distributive property worksheets is to practice. Make sure to work through several problems, and if you make any mistakes, review the concept until you understand it better.

Exploring Different Strategies for Factoring Distributive Property Worksheets: A Comprehensive Guide

Factoring distributive property worksheets can be a valuable tool to help students understand the foundational concepts of algebra. One of the most important aspects of mastering this skill is being able to recognize and implement the different strategies for factoring. This article will provide a comprehensive guide to the different strategies for factoring distributive property worksheets.

The first strategy for factoring distributive property worksheets involves the use of the distributive property itself. This strategy involves using the distributive property to simplify expressions. For example, to factor 2x(3x+7), the student would first use the distributive property to expand the expression to 6×2 + 14x. Then, the student would identify the greatest common factor (in this case, 2x) and factor it out, leaving 3x + 7 as the simplified expression.

The second strategy for factoring distributive property worksheets involves a process called “factoring by grouping”. This strategy involves dividing the expression into two or more groups of terms. For example, to factor 4y2 + 6y + 3×2 + 9x, the student would first divide the expression into two groups of terms (4y2 + 6y and 3×2 + 9x). Then, the student would factor out the greatest common factor from each of the two groups (2y and 3x). The resulting expression would be 2y(2y + 3) + 3x(3x + 3).

The third strategy for factoring distributive property worksheets involves the use of the FOIL method. This method involves multiplying two binomials together and then factoring the resulting expression. For example, to factor (x + 2)(x + 3), the student would first use the FOIL method to expand the expression to x2 + 5x + 6. Then, the student would identify the greatest common factor (in this case, x + 2) and factor it out, leaving x + 3 as the simplified expression.

The fourth strategy for factoring distributive property worksheets involves the use of the quadratic formula. The quadratic formula is used to factor equations of the form ax2 + bx + c = 0. For example, to factor x2 + 5x + 6 = 0, the student would use the quadratic formula to factor the equation into (x + 2)(x + 3) = 0.

By understanding and applying these four strategies, students will be able to successfully factor distributive property worksheets. With practice and dedication, students can master this skill and gain the confidence they need to excel in algebra.

Conclusion

In conclusion, factoring distributive property worksheets are an effective way to practice and strengthen math skills. These worksheets can be used to help students understand and apply the distributive property. They can also help students review basic algebra concepts, such as combining like terms, solving equations, and using the distributive property to simplify expressions. With practice and review, students can become more confident and proficient in their math skills.