Exploring the Benefits of Utilizing Compound Inequalities Worksheet Answers

Compound inequalities are an important mathematical tool that can be used to solve a variety of problems. Compound inequalities involve two or more inequalities that are combined, usually with the words “and” or “or.” They can be used to solve problems related to area and perimeter, as well as inequalities with multiple variables.

Utilizing compound inequalities can be beneficial in a number of ways. First, they can be used to solve equations that would be difficult to solve using just one inequality. For example, if you had an equation with two variables, it may be difficult to determine the solution using just one inequality. By combining two inequalities into one, the solution may become easier to find.

Second, compound inequalities can provide a more accurate solution than a single inequality. For example, if you have a problem that requires the use of two or more variables, it may be easier to solve it using compound inequalities rather than just one. This is because compound inequalities can provide more precise solutions, which can be more useful in solving real-world problems.

Third, compound inequalities can also be used to solve problems that involve multiple variables. For example, if you have a problem with three variables, you can use compound inequalities to solve it, rather than just one. This can be particularly useful in situations where the variables are not clearly defined, such as when solving problems in the sciences or engineering.

Finally, compound inequalities can also be used to solve problems involving area and perimeter. For example, it can be used to determine the area of a rectangle or the perimeter of a circle. By combining two or more inequalities, the solution can be found more quickly and accurately.

In summary, compound inequalities can be used to solve a variety of problems, including those involving multiple variables, area, and perimeter. By utilizing compound inequalities, the solution to a problem can be found more quickly and accurately, making it a useful tool for solving real-world problems.

A Comprehensive Guide to Understanding Compound Inequalities Worksheet Answers

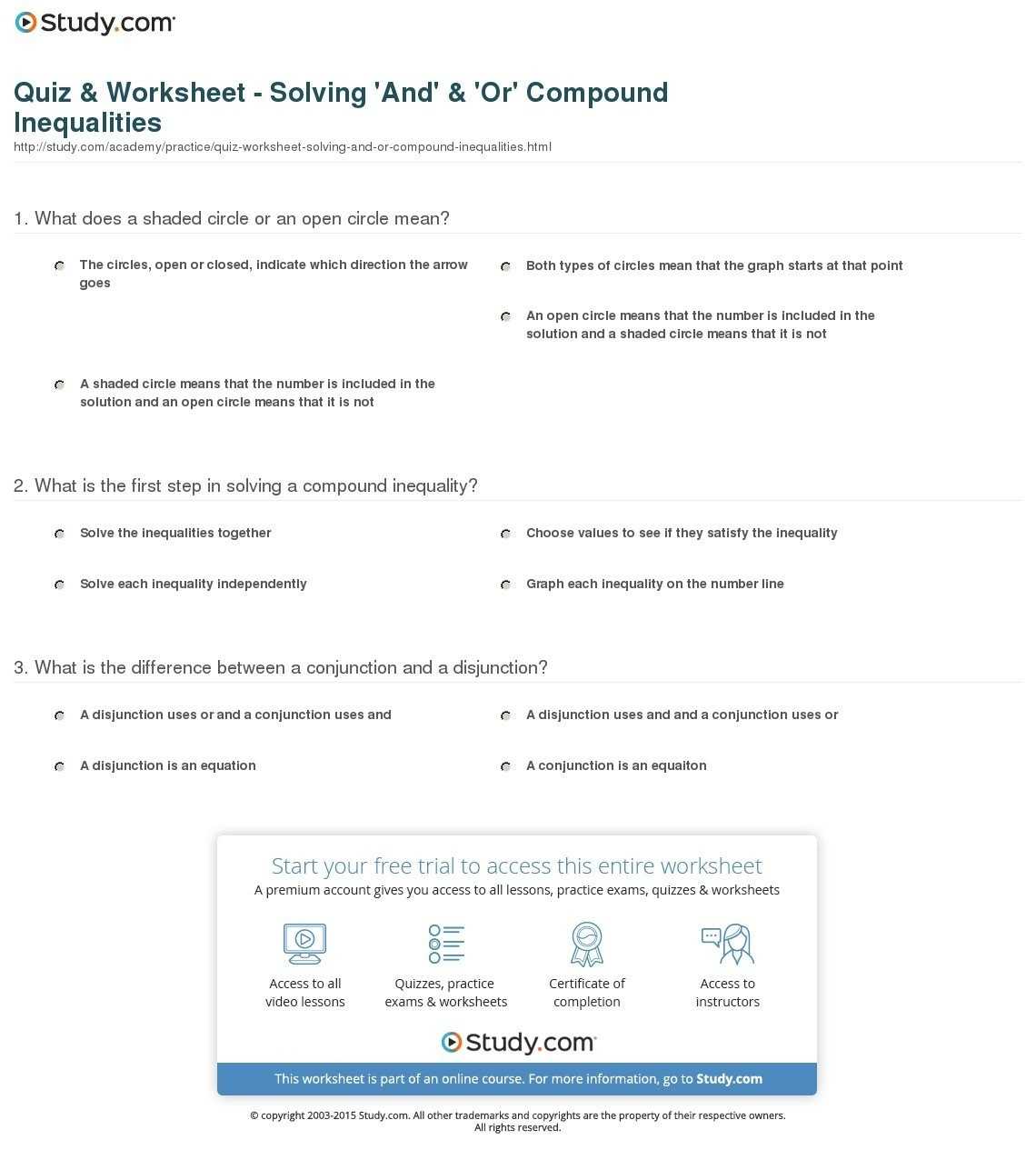
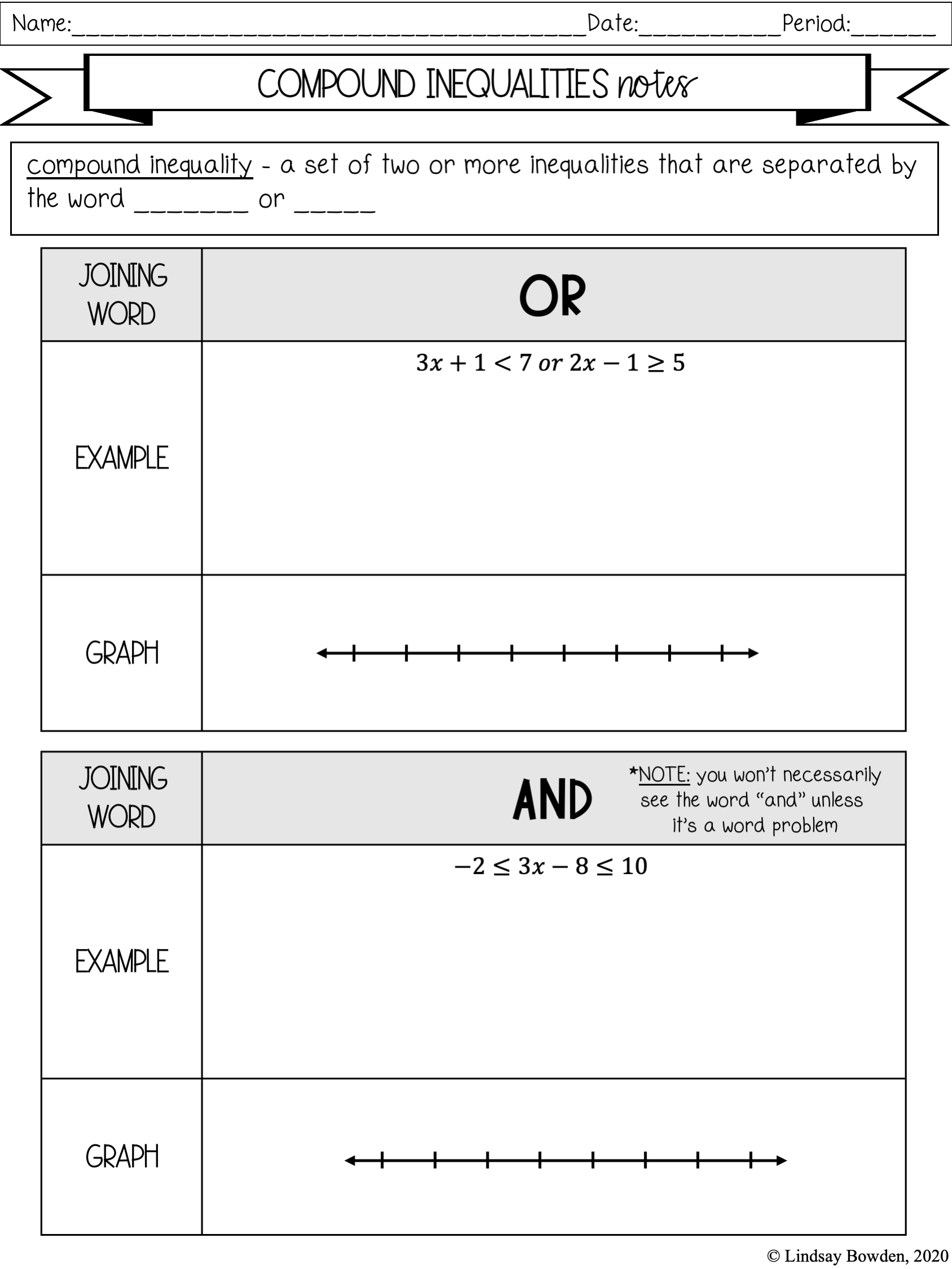
Compound inequalities are statements that involve two or more inequalities that are joined together by the words “and” or “or.” Such statements are used to express the relationship between two or more variables. In order to understand compound inequalities, it is important to be familiar with the different types that exist and how to solve them.

Type 1: Compound Inequality with “And”

A compound inequality with the word “and” is used when two inequalities are connected and both must be true in order for the overall statement to be true. For example, the statement “x > 2 and x < 6” is a compound inequality with the word “and.” In this case, the answer is all values of x that are greater than 2 and less than 6. Type 2: Compound Inequality with “Or” A compound inequality with the word “or” is used when two inequalities are connected and only one of them must be true in order for the overall statement to be true. For example, the statement “x < -3 or x > 7” is a compound inequality with the word “or.” In this case, the answer is all values of x that are less than -3 or greater than 7.

Solving Compound Inequalities

To solve a compound inequality, it is important to first identify the two inequalities and then determine how they are connected. Once this is done, the two inequalities can then be combined into one statement and solved.

For example, consider the following compound inequality: “x > 2 and x < 6.” To solve this, the two inequalities must be combined into one statement. This can be done by replacing the word “and” with an inequality symbol, such as “<.” The resulting statement would be “x > 2 < 6,” which can then be solved by finding the values of x that satisfy the statement. In this case, the answer would be all values of x that are greater than 2 and less than 6. Additional Questions 1. How do you solve a compound inequality with the word “or”? Answer: To solve a compound inequality with the word “or,” the two inequalities must be combined into one statement by replacing the word “or” with an inequality symbol, such as “<.” The resulting statement can then be solved by finding the values of x that satisfy the statement. 2. What is the difference between a compound inequality with the word “and” and a compound inequality with the word “or”? Answer: A compound inequality with the word “and” requires that both inequalities be true in order for the overall statement to be true, while a compound inequality with the word “or” requires that only one of the two inequalities be true in order for the overall statement to be true.

Leveraging Compound Inequalities Worksheet Answers for Maximum Math Performance

1. Solving compound inequalities requires a systematic approach. To begin, identify the inequality symbols and the inequality operation. Then, rewrite the inequalities as a single statement. Next, combine the inequalities into one inequality and solve for the solution.

2. To solve compound inequalities, first identify the inequality symbols and the inequality operation. Then, combine the two inequalities into one compound inequality by identifying the intersection of the two inequalities. The intersection of two inequalities is the set of solutions common to both.

3. To solve compound inequalities, first identify the inequality symbols and the inequality operation. Then, rewrite the two inequalities into one compound inequality by using the distributive property. Remember, when combining the two inequalities, the inequality sign must be flipped when multiplying or dividing by a negative number. Finally, solve for the solution.

4. To solve compound inequalities, first identify the inequality symbols and the inequality operation. Then, rewrite the two inequalities into one compound inequality by using the distributive property. Next, solve for the solution by solving each term of the inequality independently. Finally, identify the intersection of the two solutions.

5. To solve complex compound inequalities, first identify the inequality symbols and the inequality operation. Then, rewrite the two inequalities into one compound inequality by using the distributive property. Next, solve each term of the inequality independently and combine the solutions into one inequality. Finally, identify the intersection of the two solutions.

Conclusion

The Compound Inequalities Worksheet Answers provides students with a great way to practice and understand the concept of compound inequalities. By using the worksheet, students are able to review and practice the concept of solving compound inequalities and gain a better understanding of how to use them in real-world scenarios. With this practice, students can develop the skills necessary to solve compound inequalities and become more confident in their problem-solving abilities.