Breaking Down Complex Number Worksheet Answers: How to Make Sense of Challenging Problems
Complex numbers are a mathematical concept that can be difficult to understand at first. Many students find themselves struggling to make sense of the equations and formulas that are associated with this type of math. However, with the right guidance and resources, students can learn to make sense of complex numbers and become comfortable with the concepts.
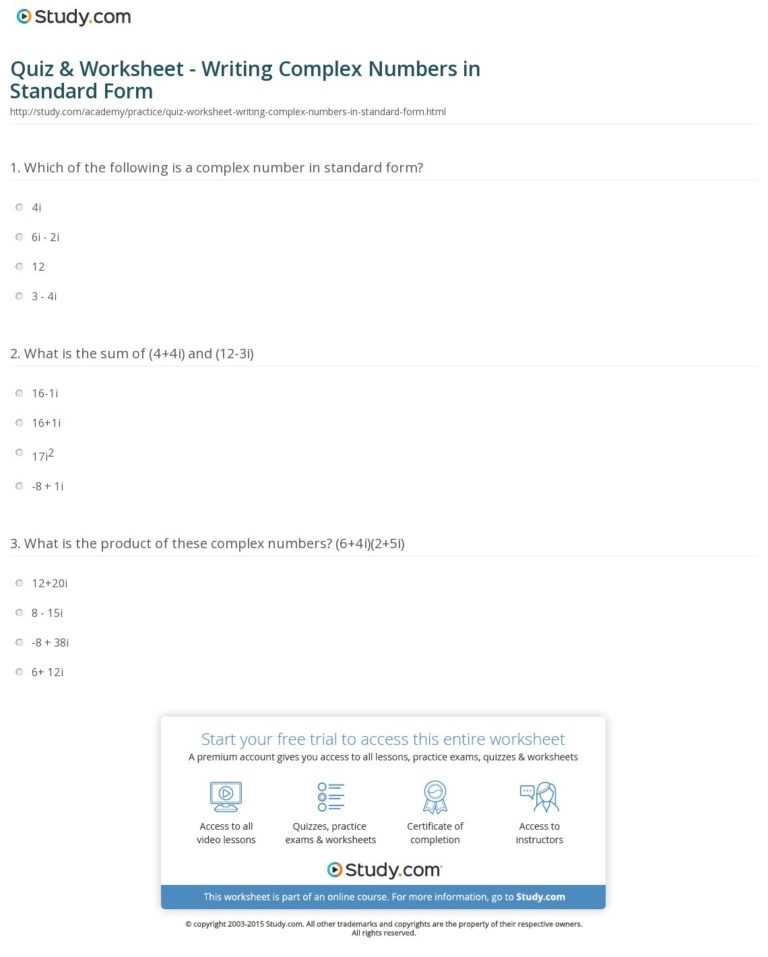
This worksheet is designed to help students break down complex number equations and make sense of them. The worksheet begins by introducing students to the concept of complex numbers and their components, such as real and imaginary numbers. Students are then asked to identify the types of operations that can be used to manipulate complex numbers and practice solving equations involving complex numbers.
Next, the worksheet moves on to more challenging problems. Students will be asked to solve equations with multiple complex numbers, including solving for multiple unknowns. They will also be asked to identify the type of equation and determine the coefficients for each number. After completing these problems, students will be able to better understand the concept of complex numbers and be better prepared for more advanced topics.
[toc]
Finally, the worksheet includes a review section that helps students to go over their work and check for mistakes. This helps to ensure that students understand the material and are able to apply it correctly.
By using this worksheet, students can make sense of complex number equations and be more confident when tackling more challenging problems. This worksheet can be used in a variety of settings, such as classrooms, online courses, and individual study. By breaking down complex number equations and working through them step by step, students will be able to gain a better understanding of this concept and be prepared to tackle more challenging problems.
Using Complex Number Worksheet Answers to Unlock the Secrets of Math
Complex numbers are an integral part of mathematical research and theory. This worksheet provides an overview of the basics of complex numbers and how they are used in mathematics. By working through the questions and answers provided, students can gain an appreciation of the power of complex numbers and how they can be applied to solve a variety of problems.
Complex numbers consist of two parts: a real part and an imaginary part. The real part is represented by a real number, while the imaginary part is represented by i, an imaginary number. This imaginary number can be raised to any power, creating complex numbers that can be written in either rectangular or polar form. In the rectangular form, a complex number is written as a + bi, where a is the real part and bi is the imaginary part. In the polar form, a complex number is written as r (cos θ + i sin θ), where r is the modulus and θ is the argument of the complex number.
The worksheet provides questions and answers about the various operations that can be performed on complex numbers, such as addition, subtraction, multiplication and division. Through these questions, students can understand the rules for performing each operation and how to apply them to solve complex problems.
The worksheet also provides questions and answers about the properties of complex numbers. These properties include the conjugate, the absolute value, and the modulus and argument of a complex number. Through these questions, students can learn how to calculate these properties and how they can be used to solve mathematical problems.
Finally, the worksheet provides questions and answers about how to graph complex numbers. Through these questions, students can understand the basic principles of graphing complex numbers and how to apply them to solve problems.
By working through the questions and answers on this worksheet, students can gain an appreciation of the power of complex numbers and how they can be used to solve a wide variety of mathematical problems. As such, this worksheet is an invaluable resource for students who are seeking to unlock the secrets of math.
The Benefits of Exploring Complex Number Worksheet Answers to Further Your Math Skills
Complex number worksheets are a great way to further your math skills and gain an appreciation for the beauty of complex numbers. They are designed to help you understand the fundamentals of complex numbers, including the fundamentals of complex conjugates, polar form, and exponential form. These worksheets also provide practice in problems that involve the use of complex numbers.
Complex number worksheets are beneficial because they allow you to explore the properties of complex numbers in a variety of ways. By working through the worksheets, you can gain an understanding of the structure and properties of complex numbers, as well as practice problem solving techniques. Through this practice, it is possible to develop an understanding of how to use complex numbers to solve problems and come up with solutions.
Complex number worksheets are also beneficial because they provide you with the opportunity to practice problem-solving skills. This enables you to become more proficient with the use of complex numbers and develop an understanding of how to use them to solve problems. Through this practice, you can gain an appreciation for the beauty of complex numbers and their mathematical applications.
The answers to complex number worksheets can also be used to further your math skills. By using the answers to the problems, you can develop an understanding of the properties of complex numbers and gain an understanding of their applications. This can help you become more proficient in using them to solve problems and develop an understanding of how to use them effectively.
Complex number worksheets can also help you gain an appreciation for the use of complex numbers in mathematics and other fields of study. By exploring complex number worksheets, you can gain an appreciation for the beauty of complex numbers and their applications. This can help you gain an understanding of how to use them effectively in problem solving and other mathematical applications.
Complex number worksheets can also help you to gain an understanding of the principles of complex numbers. By exploring the worksheets, you can gain an appreciation of the structure and properties of complex numbers and gain an understanding of their applications. This can help you become more proficient in using them to solve problems and develop an understanding of how to use them effectively.
Exploring complex number worksheets can be a great way to further your math skills and gain an appreciation for the beauty of complex numbers. By exploring the worksheets, you can gain an understanding of the fundamentals of complex numbers and their applications. Through this practice, you can gain an appreciation for the beauty of complex numbers and their applications.
Understanding the Role of Imaginary and Real Numbers in Complex Number Worksheet Answers
Imaginary and real numbers play a crucial role in complex number worksheets. Imaginary numbers are numbers that cannot be expressed as a real number, and they are represented by the letter i. Real numbers are numbers that can be expressed as a decimal, fraction, or integer. These two types of numbers are used to construct complex numbers.
A complex number is a number that combines real and imaginary components. They are represented in the form a + bi, where a is the real part and bi is the imaginary part. The real part of the complex number is always expressed as a real number, while the imaginary part is expressed as a multiple of the imaginary number i.
Complex numbers are used in mathematical operations such as addition, subtraction, multiplication, and division. To perform these operations, one must be familiar with the rules for operating with imaginary and real numbers. For example, when adding two complex numbers, the real parts are simply added together, while the imaginary parts are added using the rules of algebra. Similarly, when dividing complex numbers, the real parts are divided normally, while the imaginary parts are divided using the rules of algebra.
Complex number worksheets help students understand these operations by providing examples and practice problems. These worksheets typically involve the manipulation of both real and imaginary numbers, which allows students to gain a better understanding of how these numbers interact with each other. By mastering the rules for operating with imaginary and real numbers, students can become more confident and successful in their mathematical studies.
Examining the Interconnections Between Complex Number Worksheet Answers and Geometric Representations
Complex numbers are a fundamental concept in mathematics, with wide-reaching implications in a variety of disciplines. They are also a powerful tool for visualizing and exploring the relationship between geometric representations and algebraic equations. The complex number worksheet allows students to master the concept of complex numbers, while also developing their understanding of how these numbers can be represented geometrically.
The complex number worksheet is designed to provide students with a broad range of exercises that explore the interconnections between complex numbers and their geometric representations. The worksheet typically begins with simple problems that require students to find the real and imaginary components of a complex number. From there, students can work through a series of increasingly complex exercises that involve transformations such as translations, rotations, and reflections. Through this process, students develop an appreciation for the relationship between complex numbers and the geometric figures they represent.
The complex number worksheet also offers students a variety of ways to visualize the geometric properties of complex numbers. For example, students can use the “Polar Graph” feature to explore the relationship between the polar representation of a complex number and its corresponding Cartesian representation. This can help students understand the magnitude and direction of a number’s components and how they are related to the geometric figures they represent. Additionally, students can use the “Complex Plane” feature to explore the relationship between the real and imaginary components of a complex number and the corresponding points on a complex plane.
The complex number worksheet allows students to deepen their understanding of the interconnections between complex numbers and their geometric representations. Through this process, students become more proficient in their ability to manipulate complex numbers and their associated geometric figures. Ultimately, this process prepares students for more advanced topics in mathematics, such as calculus and topology.
Exploring the Relationship Between Complex Number Solutions and Their Graphical Representations
Complex numbers are an intriguing mathematical concept, and their graphical representations provide an insightful look into the relationship between the real and imaginary components of these numbers. This article will explore the connection between complex number solutions and their graphical representations.
Complex numbers are composed of two components: the real and the imaginary. The real component is a number on the real number line, while the imaginary component is a number on an imaginary number line. By combining the two components, a complex number is created. This number can then be used to solve various equations and problems.
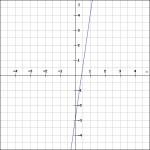
The graphical representation of complex numbers is known as the Argand diagram. This diagram consists of two perpendicular axes, known as the real and imaginary axes respectively. Each complex number is represented by a point on the Argand diagram, with the real component appearing on the real axis, and the imaginary component appearing on the imaginary axis. The origin of the Argand diagram is the point (0,0) and represents the complex number 0.
By plotting the points for a set of complex numbers on the Argand diagram, one can gain a better understanding of the relationship between the real and imaginary components of the numbers. For example, a set of complex numbers that have a positive real component and a negative imaginary component will form a line that slopes downwards from left to right on the Argand diagram. This demonstrates that the real and imaginary components of the numbers are negatively correlated.
The graphical representation of complex numbers also allows for the solution of equations and problems to be visualized. For example, when solving a quadratic equation using the quadratic formula, the solutions will be two complex numbers represented by two points on the Argand diagram. The two points will appear either on opposite sides of the origin, or in the same quadrant of the Argand diagram.
In conclusion, the graphical representations of complex numbers provide an insightful look into the relationship between the real and imaginary components of these numbers. By plotting a set of complex numbers on the Argand diagram, one can gain a better understanding of their correlation, as well as visualize the solutions to equations and problems.
Analyzing How the Different Approaches to Solving Complex Number Problems Affect the Solutions
Complex number problems often involve the manipulation of real and imaginary numbers. Different approaches to solving complex number problems can lead to varied solutions. One approach is to use the algebraic properties of complex numbers, such as the addition, subtraction, multiplication, and division of complex numbers. This approach allows the problem to be solved by manipulating the equation into a standard form and then solving for the unknown variables. Another approach is to use graphical methods, such as plotting the points on a complex plane or using trigonometric functions to visualize the solution. This approach can be advantageous in certain cases, as it gives an intuitive understanding of the problem and provides a visual representation of the solution.
Finally, the use of numerical methods is another approach to solving complex number problems. This approach involves the use of software programs or calculators to solve the problem numerically. This approach is often used when the algebraic approach is too difficult or time-consuming. Numerical methods provide an accurate solution, but may not provide insight into the underlying properties of the problem.
Each approach to solving complex number problems has benefits and drawbacks. Algebraic methods provide an insight into the underlying principles of the problem, while graphical methods provide a visual representation of the solution. Numerical methods are often used when the other two approaches are too difficult or time-consuming, but may not provide insight into the underlying principles of the problem. Ultimately, the choice of approach depends on the complexity of the problem and the desired outcome.
Practical Applications of Complex Number Worksheet Answers in Real-World Problems
Complex numbers have a range of practical applications in the real world. They can be used to solve problems in fields such as engineering, physics, mathematics, and electrical engineering.
In engineering, complex numbers can be used to solve equations which involve sinusoids or harmonics. For example, when designing a circuit containing a sine wave, engineers can use complex numbers to calculate the frequency, amplitude, and phase of the wave. This allows them to design an optimal circuit.
In physics, complex numbers can be used to solve equations which involve wave functions. For example, complex numbers can be used to solve the Schrödinger equation, which is used to describe the behavior of particles in quantum mechanics.
In mathematics, complex numbers can be used to solve equations which involve polynomials. For example, complex numbers can be used to solve the equation x^2 + 1 = 0, which has no real-number solution.
Finally, in electrical engineering, complex numbers can be used to solve equations which involve alternating currents. For example, complex numbers can be used to calculate the impedance of a circuit, which is an important factor in designing electric circuits.
Overall, complex numbers have a wide range of practical applications in the real world. They can be used to solve equations which involve sinusoids, wave functions, polynomials, and alternating currents. This makes them an invaluable tool for engineers, physicists, mathematicians, and electrical engineers alike.
Examining How Complex Number Worksheet Answers Can Help Students Improve Their Problem Solving Skills
Complex numbers are an important concept in higher-level mathematics, but many students find them difficult to understand. A complex number worksheet can be a valuable tool for helping students to learn this material. By providing practice problems and detailed answers, a complex number worksheet can help students develop their problem-solving skills.
Complex numbers have a real and imaginary component. Working with these numbers requires understanding the relationship between the two components and being able to manipulate them. A complex number worksheet can provide students with practice problems that require them to solve equations and understand the relationships between components. By working through these problems, students can develop their analytical skills and understand the concept of complex numbers better.
A complex number worksheet can also be used to help students develop their problem-solving skills. The worksheet can provide students with questions that require them to identify which operations should be used to solve a particular problem. By working through the questions, students can learn to recognize patterns and use them to identify the best way to approach a problem.
The answers to the questions on a complex number worksheet can also be used to help students learn how to approach a problem. By studying the answers, students can identify which operations were used to solve the problem and understand the steps that were taken to reach the solution. This knowledge can then be applied to other problems, helping students to develop their problem-solving skills.
Complex numbers can be a difficult concept for many students to grasp. With the help of a complex number worksheet, students can learn the material and develop their problem-solving skills. By working through practice problems and understanding the answers, students can gain the skills they need to succeed in higher-level mathematics.
Strategies for Understanding Complex Number Worksheet Answers in a Variety of Contexts
1. Become Familiar with the Basics: Before attempting to understand complex numbers in a variety of contexts, it is important to become familiar with the basics of complex numbers. Start by becoming familiar with the definition of a complex number, the imaginary unit, the operations of addition, subtraction, multiplication, division, and the properties of complex numbers. Understanding these basic concepts will make it easier to understand complex numbers in different contexts.
2. Read Examples: To gain a better understanding of complex numbers in different contexts, read examples and explanations from reliable resources. Read examples that demonstrate how to solve various problems involving complex numbers. This will help you to gain a better understanding of how to apply the concepts in different situations.
3. Practice Questions: To gain a deeper understanding of complex numbers in different contexts, practice a variety of questions. This will help you to become familiar with the types of questions that may be asked and the processes involved in solving them.
4. Visualize the Concepts: To better understand complex numbers in different contexts, it is important to be able to visualize the concepts. Try to create a visual representation of the concepts and problem-solving processes. This will help to make the concepts easier to understand and remember.
5. Work with Others: Working with a group can be a great way to gain a better understanding of complex numbers in different contexts. Working with a group can help to provide different perspectives on the concepts and can help to fill in any gaps in understanding.
6. Ask Questions: Asking questions can be a great way to gain a better understanding of complex numbers in different contexts. Ask questions of your instructor, classmates, or others who are knowledgeable in the field. This will help to ensure that you have a complete understanding of the concepts and processes involved.
Conclusion
The Complex Numbers Worksheet Answers is a great resource for students to gain an understanding of how to work with complex numbers. It provides step-by-step instructions on how to solve problems involving complex numbers, as well as an overview of the different types of operations that can be performed on them. It is an invaluable tool for students to gain an understanding of the fundamentals of mathematics, particularly in the area of complex numbers.
[addtoany]